Cm 1 Classical Mechanics By Goldstein

of 9
M.Sc Physics Previous Kh. Fareed Govt. P/G College RYK
Mechanics:The Branch of physics which deals with the state of rest or motion of bodies under
the action of forces is called Mechanics
It has three main branches
Kinematics:The branch of mechanics which deals with the phenomenon of motion without
reference to mass and force. The motion may be translational, vibrational or rotational.
Dynamics:The branch of mechanics which deals with the laws that tells us under certain
conditions that what type of motion is possible. It also deals with the causes of motion and
thereby introduce the causes of force.
Statistics:The branch of mechanics which deals with the motion of atomic size particles.
Classical Mechanics (Newtonian Mechanics)
The branch of Mechanics which deals with the motion of bodies having not small
masses. It is computational scheme regarding the interaction of force and motion.
The branch of mechanics which is based on Newton’s Laws of motion is called Classical
Mechanics or Newtonian Mechanics.
The entire study of Classical mechanics can be divided into two branches
1) Problem Concerning to the motion of single particles
2) Problem concerning to the motion of system of particles (Rigid body is only spherical
case of a system of particles.
The laws, principals and formulation developed by various scientists are called tools of
mechanics.
For analyzing the moving behavior of particle or the system of particles, the tools are
(i) Newton’s Law
(ii) Lagrangian Mechanics
(iii) Hamilton’s Formulation
Drawbacks of Classical Mechanics
Classical Mechanics is unable to explain

of 9
1. Motion of objects moving at speed closed to speed of light.
2. Motion of Microscopic particles inside the atoms and molecules.
To resolve these issues new platforms are introduced
Relativistic Mechanic:
Relativistic Mechanics describes the motion of particles moving at speed closed to
speed of light.
Quantum Mechanics:
Quantum Mechanics describes the motion of particles at microscopic level.
Newton’s First Law of Motion (Law of Inertia)
In the absence of forces particle move with constant Velocity. OR
“In the absence of any forces, a stationary particle remains stationary and moving particle
continue to move with unchanged speed in the same direction” OR
“In the absence of force, particle has no acceleration”
i-e ∑ =
Frame of reference:A set of coordinate axis with respect to which measurements can be
made is called a frame of reference.
Inertial frame of reference.
The frame of reference, in which Newton’s First Law of motion holds, is known as inertial frame
of reference.
A frame of reference stationed on earth is approximately an inertial frame of reference
Force :A force move or tends to move stops or tends to stop the motion of body, it can also
change the direction of motion of a body.
Internal Forces:The force which is exerted by a molecule or particles to the rest of molecules
or particles is called internal forces.
External Forces:The force which is exerted by a body to the other body is called External force.

of 9
Newton’s Second Law of Motion
“For any particle of mass m, the net force on the particle is always equal to mass times
the particle acceleration” =
In this Equation, F denotes the vector sum of all the forces on the particle and “a” is particles
acceleration.
“For a particle of mass “m”, the net force on a body is equal to rate of change of
momentum”
= =
Newton’s 3rd
Law of Motion
“Every force on an object inevitably (without doubt) involves a second object, the object that
exerts a force”
→ 2 1
→ 1 2
“If object 1 exerts a force on object 2, then object 2 always exerts a reaction force
on object 1 is given by
= −
Central Force: “The force act along the line joining centers.”
Generallalized Coordinates:When we discuss the configuration of the system we select the
smallest possible number of variables called generallized coordinates. OR
“Minimum no. of coordinates to specify the system”

of 9
Question: Derive the conservation theorem of Linear momentum, Angular Momentum
and energy for a single Particle?
Mechanics of a single Particle
Consider a single particle of mass “m” is moving along a certain path as shown in fig
Let at time “t” its position w.r.t to origin is “r”. Now the velocity of
particle at point z is
=
If m is the mass of particle, then its linear momentum is
=
As long as particle moves, it experiences a certain force. This force may be
1) As a result of interaction between two particles
2) As a result of interaction of electric field
3) As a result of interaction of magnetic field
Suppose F is the force acting on the particle as a result of interaction, then according to
Newton’s 2nd
Law of motion in terms of momentum
=
As = So
= = ( ) = =
Where “a” is called acceleration of particle.
If there is no force on a particle then = 0So
=
In the absence of external forces, the total momentum of system is constant,
this is called Law of conservation of momentum.

of 9
Angular Momentum
The angular momentum L of a single particle is
defined as the vector
= ×
Here × is the vector product of the particles position vector
r, relative to the chosen Origin O and its momentum is P.
Since r depends on the choice of origin, so N is also depends on
the origin.
The time rate of change of angular momentum N is
= ( × ) = ( × ) + ( × ) = ( × ) + ( × )
( × ) = Because, a body cannot rotate about its own axis. So
= × =
Rate of change of angular momentum is equal to torque.
Conservation of Angular Momentum
We know that Torque N of a particle about “O” is
= ×
Where = So the above equation becomes
= × = ×
( )
= ( × )
= × + × ( )
= × + ×
× = .
= ×

of 9
= ( × ) = ( × )
As ( × ) = so
= ( )
If torque acting on a body is zero i-e =
( ) =
On integrating, we get =
If the total toque acting on a system is zero, then systems total angular momentum iz
constant. This is called “Principal/Law of conservation of angular momentum”
Conditions for a Force to be Conservative
A force F acting on a particle is conservative if and only if it satisfies two conditions
1) F depends only on the particles position r that is = ( )
2) For any two points 1 and 2, the work done by F is the same for all paths between 1 and
2.
Second condition for a Force to conservative
To know that the force is conservative or not we use a test, which is
× =
If the force fulfills this condition, we say that the force is conservative, otherwise not.

of 9
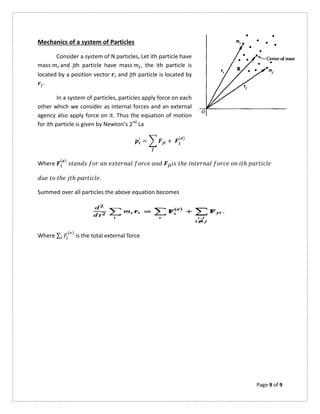
Law of conservation of Energy
It states that
If the force acting on a particle is conserved, then total energy of the particle is conserved.
i-e Sum of K.E and P.E is conserved. OR
Proof:
Let a particle be moving from point 1 to another Point 2 under the conservative field
force. The work done in going from point 1 to point 2 is
= .
= . = . = . = .
=
2
=
1
2
( − ) =
1
2
−
1
2
= − → ( )
Work done is equal to Change in Kinetic Energy.
As we know that Work done around a closed path is zero. If “V” is the potential energy
of the particle, then F is the gradient of this scalar function
= − − − − −(1)
By Stokes Theorem, the condition of conservative force becomes
× =
Multiplying both sides of (1) by ds
. = − .
. = −
Ձ
Ձ
+
Ձ
Ձ
+
Ձ
Ձ
. [ + + ]

of 9
. = −
Ձ
Ձ
+
Ձ
Ձ
+
Ձ
Ձ
. = −
Thus = ∫ . = ∫ − = −( )
= −( − ) = − → ( )
From (A) & (B)
− = −
+ = +
i-e If the force acting on a particle is conservative, then the total energy (T+V) is conservative.
This is the Law of Conservation of Energy.
OR
If a conservative force F acts on the system, then the total energy of the system remains
conserved and change in total energy is always equal to zero.

of 9
Mechanics of a system of Particles
Consider a system of N particles, Let ith particle have
mass and jth particle have mass , the ith particle is
located by a position vector and jth particle is located by
.
In a system of particles, particles apply force on each
other which we consider as internal forces and an external
agency also apply force on it. Thus the equation of motion
for ith particle is given by Newton’s 2nd
La
= +
( )
Where
( )
ℎ ℎ
ℎ ℎ .
Summed over all particles the above equation becomes
Where ∑ ( )
is the total external force

Cm 1 Classical Mechanics By Goldstein

More Related Content

What's hot

Similar to Cm 1 Classical Mechanics By Goldstein

More from AmeenSoomro1

Recently uploaded

Cm 1 Classical Mechanics By Goldstein