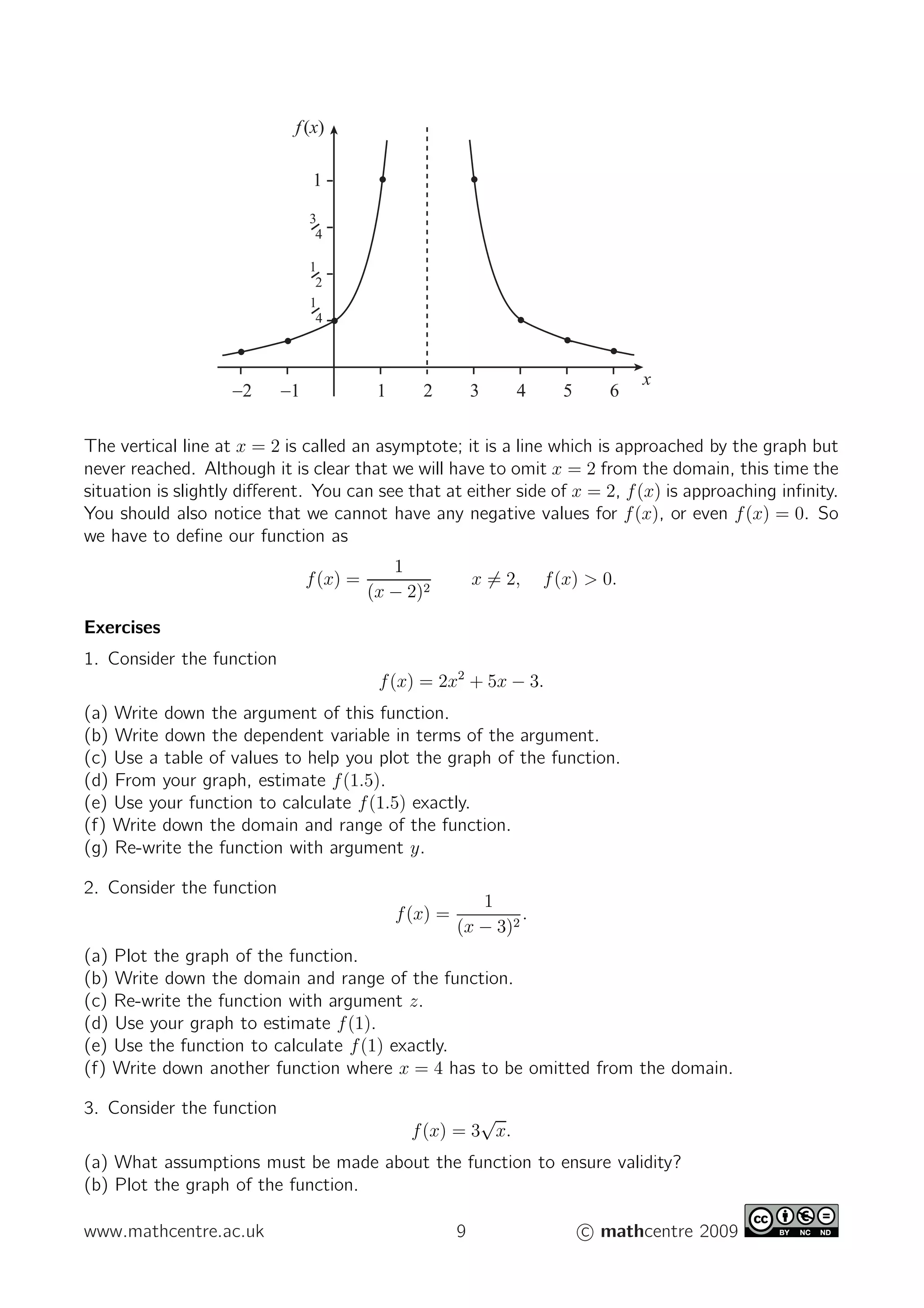
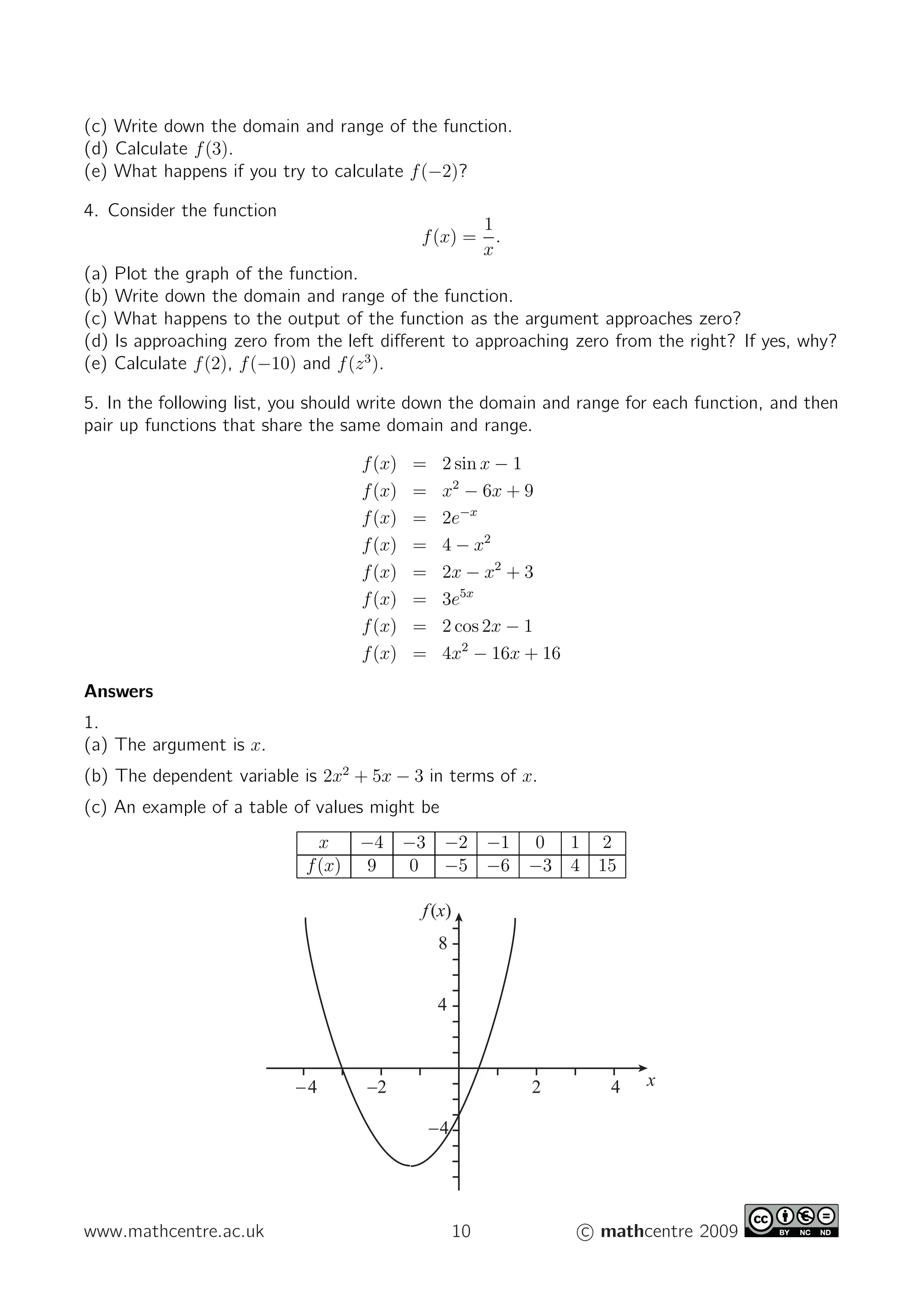
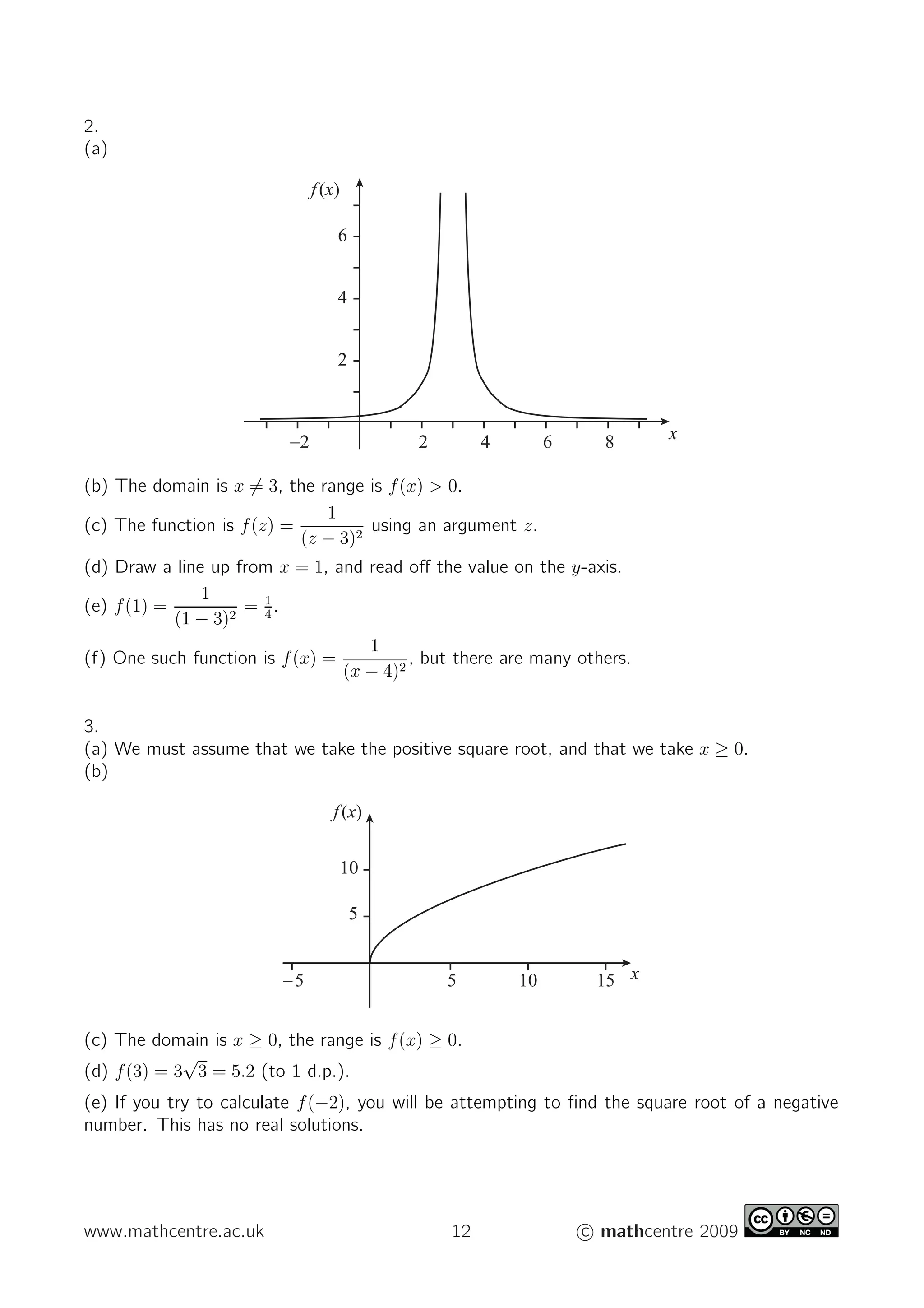
- A function is a rule that maps an input number (independent variable) to a unique output number (dependent variable).
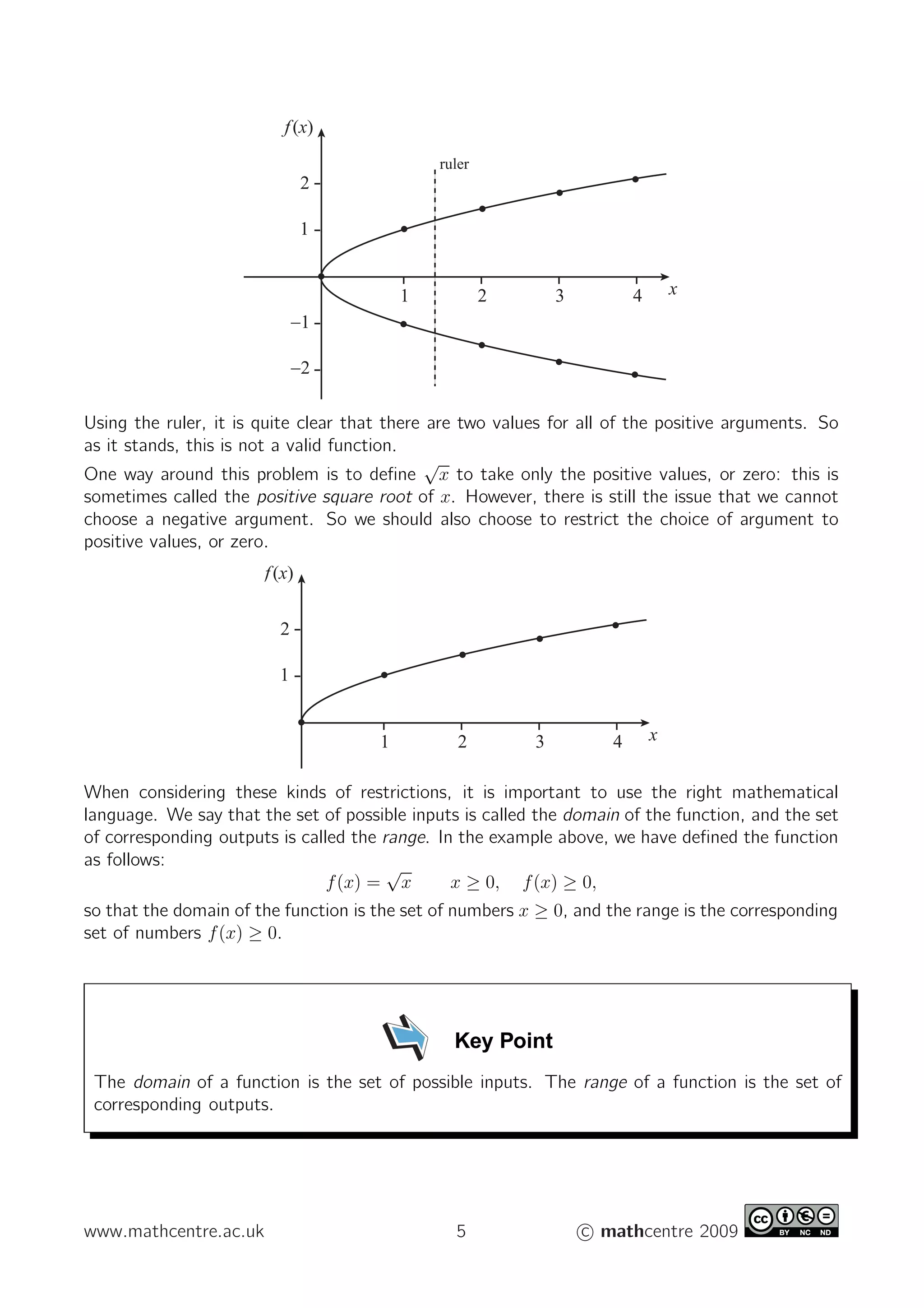
- To determine if a rule describes a valid function, you can plot points from the rule on a graph and check that each input only maps to one output using a vertical ruler.
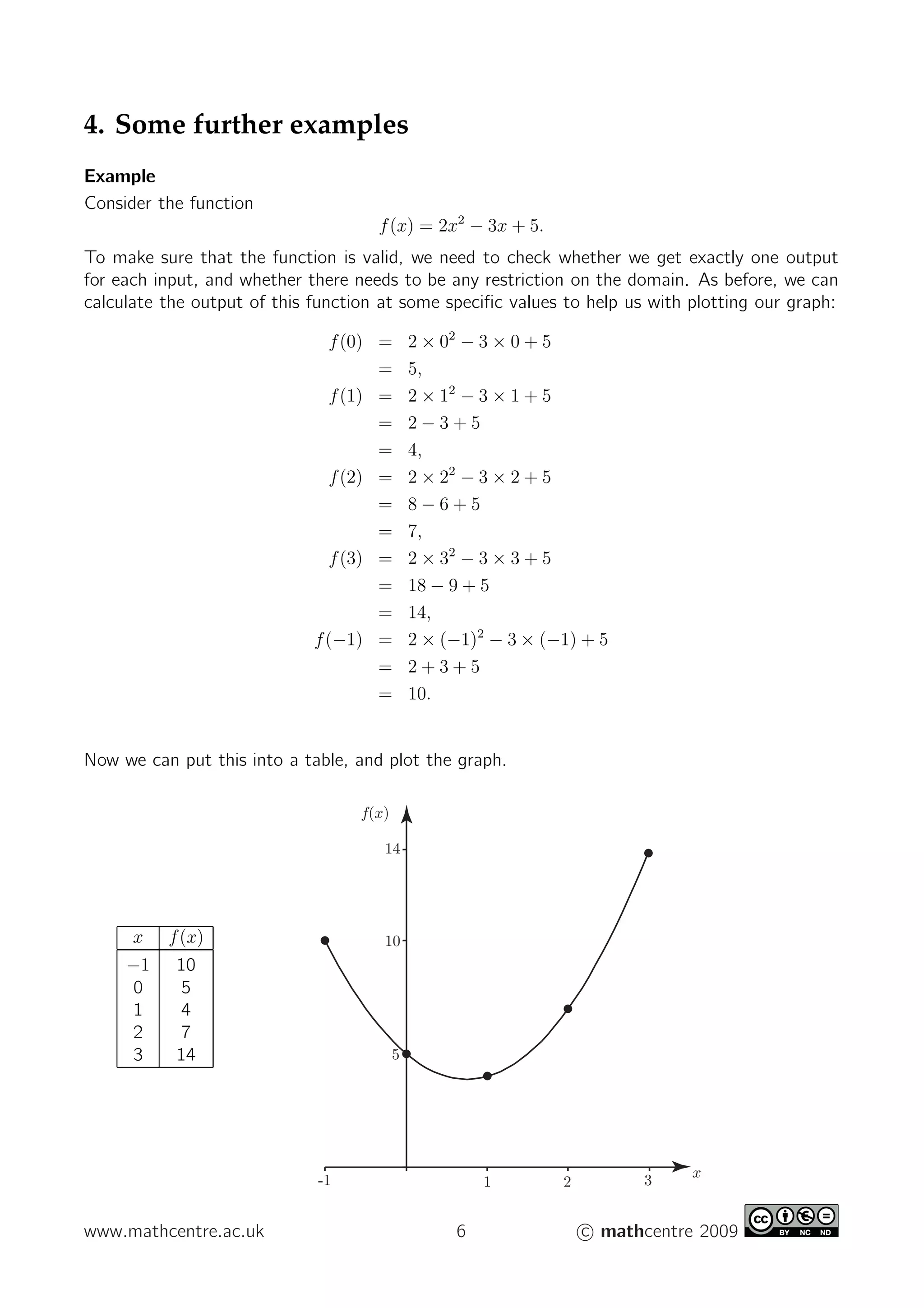
- For a rule to describe a valid function, its domain must be restricted if multiple outputs are possible for any single input. The domain is the set of possible inputs, and the range is the set of corresponding outputs.