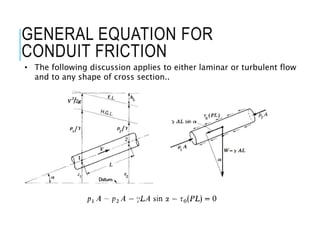
This document discusses laminar flow in pipes. It introduces that piping systems are commonly studied in engineering. For laminar flow, velocity alone does not determine if flow is laminar or turbulent, there are three flow regimes based on Reynolds number: laminar, transition, and turbulent flow. The critical Reynolds number that defines the transition between laminar and turbulent flow is around 2,000. For non-circular pipes, hydraulic radius replaces diameter in Reynolds number calculations. The document then discusses equations for conduit friction loss and laminar flow in pipes specifically.

1. FLUID MECHANICS-II
LEC #3: LAMINAR FLOW IN
PIPES
Dr. M.
Mubashir
Qureshi

2. INTRODUCTION
Piping systems are encountered
in almost every engineering
design and thus have been
studied extensively.
There is a small amount of
theory plus a large amount of
experimentation.
The basic piping problem is this:
Given the pipe geometry and its
added components (such as
fittings, valves, bends, and
diffusers) plus the desired flow
rate and fluid properties, what
pressure drop is needed to drive
the flow.

3. LAMINAR FLOW
• Incompressible Fluids. p = constant
• Velocity and laminar flow
• Velocity is not the only factor that determines whether
the flow is laminar or turbulent
The three regimes of flow: (a) laminar flow at low Re;
(b) transition at intermediate Re; (c) turbulent flow at

4. CRITICAL REYNOLDS NUMBER
• R value is normally about 4,000, but
laminar flow in circular pipes has been
maintained up to values of R as high as
50,000.
• It is practically impossible for turbulent
flow in a straight pipe to persist at values
of R much below 2,000.
• Hence this lower value of R = 2000 will be
defined as the true critical Reynolds
number.

5. HYDRAULIC RADIUS
• For conduits having noncircular cross
sections, some value other than the
diameter must be used for the linear
dimension in the Reynolds number.
• Such a characteristic is the hydraulic
radius, defined as Rh = A / P. Where A
is the cross-sectional area of the
flowing fluid, and P is the wetted
perimeter
• Rh = D/4 for circular pipes so D = 4Rh
is used in equation of Reynold
number.
𝑅 =
𝑉𝐷𝜌
𝜇

7. GENERAL EQUATION FOR
CONDUIT FRICTION
• The following discussion applies to either laminar or turbulent flow
and to any shape of cross section..

8. GENERAL EQUATION FOR
CONDUIT FRICTION

9. GENERAL EQUATION FOR
CONDUIT FRICTION
Dimensional Analysis for Smooth
Conduits

10. PIPES OF CIRCULAR CROSS
SECTION
Equation above known as the equation of
pipe friction, and is also commonly referred
to as the Darcy-Weisbach equation.

11. LAMINAR FLOW IN PIPES

12. LAMINAR FLOW IN PIPES
The striking feature of this equation is that it involves no empirical
coefficients or experimental factors of any kind, except for the physical
properties of the fluid such as viscosity and density (or specific weight).
From this it would appear that in laminar flow the friction is independent
of the roughness of the pipe wall.

13. LAMINAR FLOW IN PIPES

14. ENTRANCE CONDITIONS IN
LAMINAR FLOW

16. https://www.youtube.com/watch?v=kmjFdBxbV08