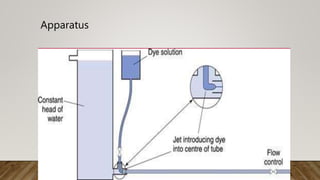
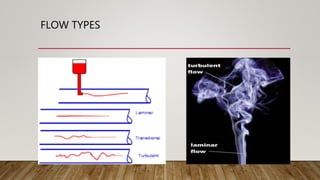
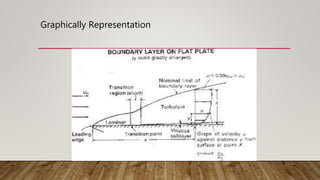
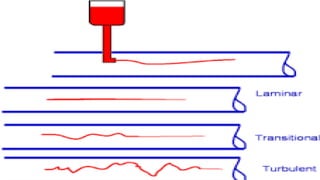
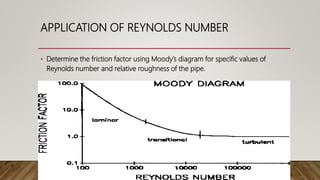
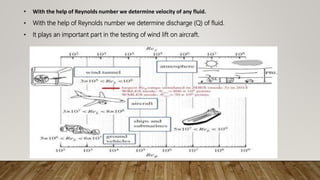
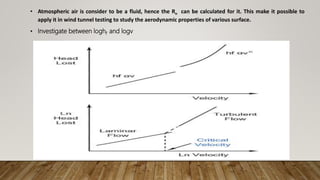
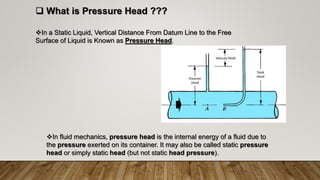
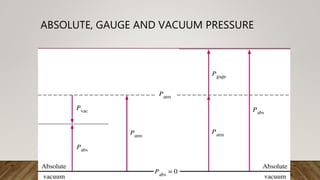
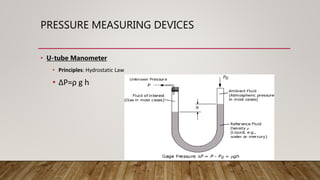
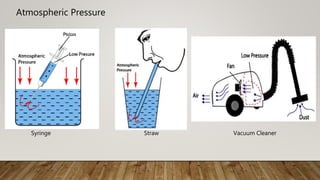
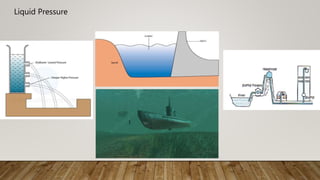
This document presents information about Reynolds number and pressure head. It was presented by 4 students to their teacher. It defines Reynolds number and describes different types based on flow conditions. It also explains pressure head and different types of pressure like absolute, gauge and vacuum pressure. Various pressure measuring devices are discussed along with their principles and applications. Examples of applications of Reynolds number and pressure head in different fields like fluid mechanics and engineering are also provided.

2. Presented To:
Honorable Teacher
Sir Engr. Muneeb
Presented By:
Sajid Ghafoor (2kx5-103)
Muhammad Shahid (2kx5-105)
Salman Hafeez (2kx5-106)
Hasnain Saeed (2kx5-116)

3. CONTENTS:
• Reynolds Number
• Definition
• Types
• Experiment
• Applications
• Pressure Head
• Definition
• Types
• Instruments & Measurements
• Application

4. REYNOLDS NUMBER

5. REYNOLDS NUMBERS
What is Reynolds Number?
The ratio between the internal forces and viscous forces.

6. CONDITIONS.
• For laminar Re < 2000.
• For transition Re >2000 <4000.
• For turbulent Re>4000.

7. REYNOLDS EXPERIMENT
• Apparatus
• Water tank.
• Glass tube.
• Color dye.
• Value.

8. Apparatus

9. PROCEDURE
• Take water in container.
• Attach glass tube.
• Colour dye.
• Open the valve .
• Analyze the flow.

10. FLOW TYPES

11. Graphically Representation

12. Graphically
• Critical point
It is a point on which flow change from laminar to turbulent flow.
• True critical point
It is a point below which flow is always laminar maximum value is
1999.99

13. Conclusion
• For laminar flow
pressure head loss is directly proportional to velocity.
• For turbulent flow
pressure head loss is directly proportional to the square of velocity
( Where n varies from 1.75 from 2 )

14. Uses & Application

16. APPLICATION OF REYNOLDS NUMBER
• Determine the friction factor using Moody’s diagram for specific values of
Reynolds number and relative roughness of the pipe.

17. • With the help of Reynolds number we determine velocity of any fluid.
• With the help of Reynolds number we determine discharge (Q) of fluid.
• It plays an important part in the testing of wind lift on aircraft.

18. • Atmospheric air is consider to be a fluid, hence the Rn can be calculated for it. This make it possible to
apply it in wind tunnel testing to study the aerodynamic properties of various surface.
• Investigate between loghf and logv

19. • By the help of Reynolds number we control failure of fluid structure.
• Swimming pool design

20. PRESSURE HEAD

21.  Pressure is defined as a normal force exerted by a fluid per unit area.
 Pressure is the force per unit area, where the force is perpendicular to
the area.
 Units of pressure are N/m2, which is called a Pascal (Pa).
 Since the unit of Pa is too small..! For pressures Encountered in
practice kilopascal (1 KPa = 103 Pa) and megapascal (1 MPa = 106
Pa) are commonly used.
p=
A
m2
Nm-2
(Pa)
N
F
pa= 105 Nm-2
1psi
=6895Pa
1 psi = 1 lbf ( 1 in ) 2 ≈ 4.4482 N (
0.0254 m ) 2 ≈ 6894.757 Nm-2
What is Pressure?

22. Pressure in a fluid acts equally in all directions.
Pressure in a static liquid increases linearly with depth
P=
Increase
In Depth
(M)
Pressure
Increase
GH
The pressure at a given depth in a continuous, static
body of liquid is constant.
p1
p2
p3 p1 = p2 = p3

23. Fluid exerts forces in many directions. Try to submerse
a rubber ball in water to see that an upward force acts on
the ball.
Fluids exert pressure in all
directions.
 Fluid Pressure
F

24.  Properties of Fluid Pressure
Water seeks its own level, indicating that
fluid pressure is independent of area and
shape of its container.
At any depth h below the surface of the
water in any column, the pressure P is the
same. The shape and area are not
factors.
 The forces exerted by a fluid on the walls of its container are
always perpendicular.
 The fluid pressure is directly proportional to the depth of the fluid
and to its density.
 At any particular depth, the fluid pressure is the same in all
directions.
 Fluid pressure is independent of the shape or area of its container.

25.  What is Pressure Head ???
In a Static Liquid, Vertical Distance From Datum Line to the Free
Surface of Liquid is Known as Pressure Head.
In fluid mechanics, pressure head is the internal energy of a fluid due to
the pressure exerted on its container. It may also be called static pressure
head or simply static head (but not static head pressure).

26.  What is Pressure at a Point ?
Pressure at any point in a fluid is the same in all
directions.
Pressure has a magnitude, but not a specific direction,
and thus it is a scalar quantity.

27. Pressure Variation In A Fluid At Rest
; ;
mg
P m V V Ah
A
  
Vg Ahg
P
A A
 
  h
mg
Area
P = gh
• Pressure at any point in a fluid is directly
proportional to the density of the fluid and
to the depth in the fluid.

28. 1. Absolute Pressure
2. Gage Pressure
3. Vacuum Pressure
Types Of Pressure
Absolute Pressure
Absolute Pressure: The sum of the pressure
due to a fluid and the pressure due to
atmosphere.
Gauge Pressure: The difference between the
absolute pressure and the pressure due to the
atmosphere:
Absolute Pressure = Gauge Pressure + 1 atm
h
P = 196 kPa
1 atm = 101.3 kPa

29. Vacuum
Pressure
One way to measure atmospheric pressure is to
fill a test tube with mercury, then invert it into a
bowl of mercury.
Pressure below atmospheric pressure are called
vacuum pressure, Pvac=Patm - Pabs.
Gage Pressure
 Most pressure-measuring devices are calibrated to read zero in the
atmosphere, and therefore indicate gage pressure, Pgage=Pabs - Patm.

30. ABSOLUTE, GAUGE AND VACUUM PRESSURE

31. PRESSURE MEASURING DEVICES
• Bourdon Gage:
• Principles: change in curvature of the tube is proportional to difference of pressure inside
from that outside the tube
• Applications: tire pressure, pressure at the top or along the walls of tanks or
vessels

32. PRESSURE MEASURING DEVICES
• Strain Gage
• Principles: ∆ P  ∆ Resistance  ∆ Voltage
• Applications: Sensors for internal combustion engines, automotive, research etc.

33. PRESSURE MEASURING DEVICES
• Quartz Gage
• Principles: ∆ Pressure  ∆ Charge  ∆ Voltage
• Applications: measurements with high accuracy, good repeatability, high resolution. e g.
Quartz Clock

34. PRESSURE MEASURING DEVICES
• Piezoresistive Gage
• Principles: ∆Pressure = ∆Charge = ∆Resistance = ∆Voltage
• Applications: Very accurate for small pressure differentials.
e.g. Difference between indoor and outdoor pressure
Digital Manometer

35. PRESSURE MEASURING DEVICES
• U-tube Manometer
• Principles: Hydrostatic Law
• ∆P=ρ g h

36. PRESSURE MEASURING DEVICES
• U-tube Manometer
• Applications: air pressure, pipe pressure, etc.
Air Water ManometerMercury Water Manometer

37. PRESSURE MEASURING DEVICES
• UT Manometer Applet

38. Applications

39. Syringe Straw Vacuum Cleaner
Atmospheric Pressure

40. Liquid Pressure