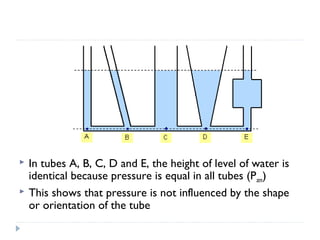
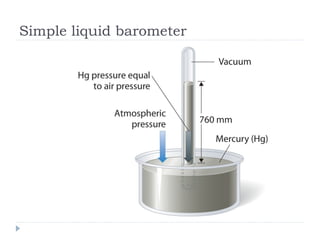
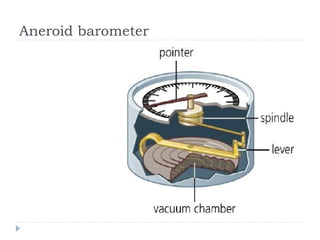
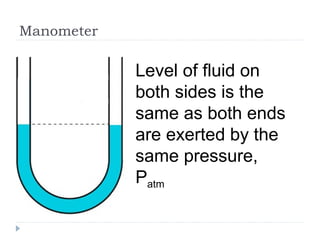
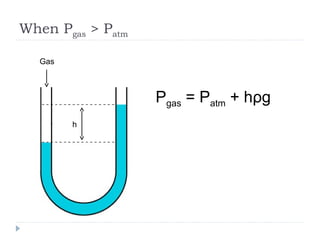
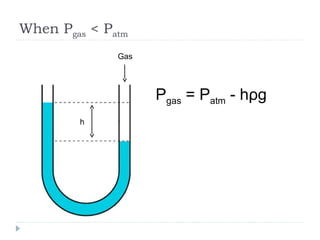
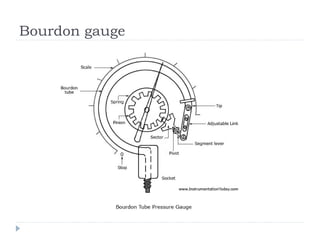
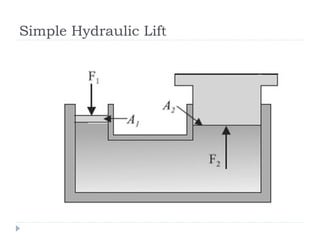
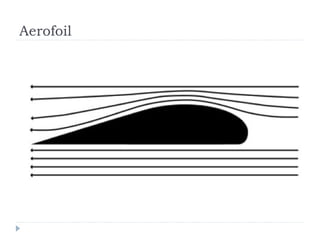
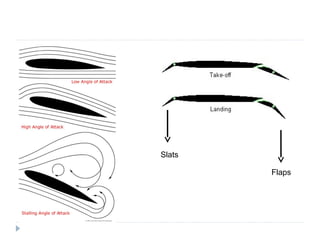
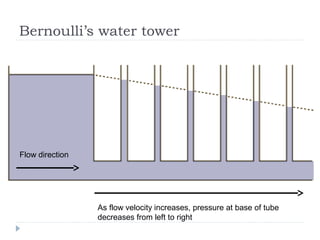
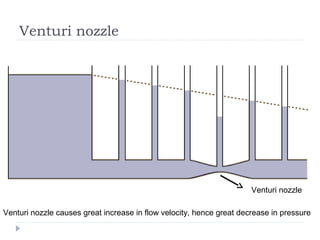
Solid pressure is defined as the force acting on a given area, measured in Pascals. Fluid pressure results from particle collisions within the fluid and increases with depth and density. It is described by the equation P=hρg. Atmospheric pressure decreases with altitude and is measured using barometers. Fluids transfer pressure equally in all directions according to Pascal's principle, which has applications in hydraulic systems. Archimedes' principle describes buoyancy as the upward force equal to the weight of fluid displaced. Bernoulli's principle states that fluid pressure decreases where velocity increases, as seen in aerofoils, venturi nozzles, and other streamlined objects.

1. Solid And Fluid Pressure
Form 4 Physics (SPM) – Chapter 3

2. Solid Pressure




Magnitude of force acting on a given area
Pressure, P = Force, F / Area, A
unit = Nm-2 or
Pascal, Pa
Although force is a vector quantity, pressure is a scalar
quantity.
This is because experimentally, pressure acts equally in all
directions, producing no net direction

3. Fluid Pressure





Pressure that results from the collision of particles in
fluid
Particle collision are mostly elastic, thus conserving
kinetic energy and momentum (mv)
The change in direction after collision results in a rate of
change in momentum, producing impulsive force.
This force acts on a given area, produces pressure
Increasing depth of fluid (amount of fluid) and its density
increases particle collision, resulting in increasing
pressure

4. 


Pressure, P = h ρ g where depth of fluid = h, density of
fluid = ρ, acceleration due to gravity = g
Unit = kgm-1s-2 or Pascal (Pa)
Other units commonly used:




PSI (pounds per square inch) – Imperial system
Bar
atm (where 1 atm = 105 Pa = 76cmHg)
mmHg/cmHg/mmH2O/cmH2O

5. Atmospheric Pressure (Patm)

Pressure exerted by the particles in the atmosphere on
every surface on Earth
Changes with altitude because the density of the
atmosphere changes with altitude. (Density and therefore
pressure decreases as altitude increases)
Patm at sea level (average height of ocean) ≈1 X 105 Pa

Patm at peak of Mt. Everest ≈3.33 X 104 Pa



6. 

In tubes A, B, C, D and E, the height of level of water is
identical because pressure is equal in all tubes (P atm)
This shows that pressure is not influenced by the shape
or orientation of the tube

7. 

The instrument used to measure atmospheric pressure is
known as a barometer. (Baro = pressure)
Types of barometers:


Mercury barometer
Aneroid barometer

8. Simple liquid barometer

9. 
Fluid used in barometer has to have the following
properties:




Incompressible
Does not evaporate easily
Does not stick to the wall of the barometer
Ideal fluid to be used is mercury (Hg)

10. 
Atmospheric pressure is measured by
Patm = <Height of column><Name of fluid>
Patm = 76cmHg

To convert cmHg to the S.I. unit, Pa:
Patm = hρg
Patm = (76/100) X 1.36x103(density of Hg) X 10
Patm = 1x105 Pa

11. 
If water is used in substitute for mercury, the column
height can be calculated:
Patm = hρg
1x105 = h X 1x103 X 10
105 = h X 104
h = 10m

Having a column height of 10m makes the water
barometer unfitting and immobile.

12. Aneroid barometer

13. 
Atmospheric pressure is applied in:






Sucker hooks
Drinking straws
Evaluating altitude (altimeter)
Baking with yeast
Breathing
Heimlich maneuver

14. Gas pressure (Pgas)



Pressure exerted by gas particles on surrounding surfaces
Measured by an instrument known as a manometer (Utube)
In a manometer, the fluid pressure at one point in one
arm is equal to the pressure at another point in the
opposite arm at the same level, where the type of fluid is
the same

15. Manometer
Level of fluid on
both sides is the
same as both ends
are exerted by the
same pressure,
Patm

16. When Pgas > Patm
Gas
Pgas = Patm + hρg
h

17. When Pgas < Patm
Gas
Pgas = Patm - hρg
h

18. Bourdon gauge

19. Transfer of pressure within static fluid



When an object is submerged in a fluid, it experiences
equal pressure from all directions. The pressure is
transferred equally in the fluid in all directions.
Hence, neglecting pressure changes due to depth, the
pressure at any given point within the fluid is constant.
Pascal’s Principle


In a closed system of fluids, any pressure exerted is equally
distributed throughout the fluid and remains constant
Characteristics of the hydraulic fluid:



Incompressible
Does not adhere to the surface of the system
Is not volatile

20. Simple Hydraulic Lift

21. 
Since pressure is evenly distributed,
P 1 = P2
Thus,
F1/A1 = F2/A2

When one piston is depressed, the other piston rises.
This occurs as the volume displaced by the fluid from the
first piston occupies the space at the second piston
V1 = V 2
Thus,
d1A1 = d2A2
where A = surface area of piston, d = distance moved by
piston

22. 
Applications of Pascal’s Principle:



Hydraulic jacks
Hydraulic robots and machinery
Vehicle brakes and steering

23. Support due to pressure in fluids




With reference to Newton’s Law of Motion, every action
of force has a normal that acts in the opposing direction.
Weight is a force and has a normal support on solid
ground. When an object is immersed in fluid, the normal
support is produced from the pressure differential at the
upper and lower surface of the object.
This supportive force provides floatation and is known as
buoyancy.
Archimedes’ Principle

When an object is partially or completely immersed in a fluid,
the weight of the fluid displaced is equivalent to the buoyant
force that supports the object

24. 

Buoyant force, B = V ρ g, where V volume of immersed
part of the object, ρ = density of fluid, g = acceleration
due to gravity
Buoyant force is also equivalent to weight of object when
not immersed (true weight) – weight of object when
immersed (apparent weight)
B = Wt - Wa

An object sinks when Wt > B

An object floats when Wt = B

25. 


In a uniformly distributed fluid, buoyant force remains
constant regardless of depth of fluid.
Buoyant force changes in direct proportion to fluid
density.
Fluid density increases when




Temperature decreases
Concentration increases
Pressure increases
Mass increases

26. 
Applications on Archimedes’ Principle






Submarine
Plimsoll Scale on the hull ships
Hot air balloon
Hydrometer
Cartesian diver
Measuring volume of kings’ crowns using a bath tub and an old
genius

27. Differential pressure in fluid flow
High fluid pressure
Fp
Low fluid pressure
vt
vf
Direction of motion

28. 
Imagine a particle moving uniformly in a fluid of gradually
decreasing pressure. The pressure behind the particle is
greater than the pressure in front.

A force (Fp)will be produced in the direction of motion
resulting in acceleration of the particle, thus the velocity
of the accelerating particle at the back (vt) is greater than
at the front (vf).

This shows that pressure and velocity are inversely
related
Bernoulli’s Principle


Pressure and velocity of a fluid are inversely proportional as a
result of the fluid flowing in a curved streamline.

29. Aerofoil

30. 




In fluid mechanics, it is generally accepted that liquids and
gases flow in arranged packets known as streamlines.
An aerofoil has an aerodynamic shape which is meant to
redirect air streamlines in order to minimise resistance
and produce lift
Curvature of the streamline occurs when the air is
passed above the aerofoil due to the shape of the
aerofoil.
The curvature decreases the air velocity of the streamline
above the aerofoil resulting in the pressure below the
aerofoil to be greater than above.
The differential pressure produces the aerodynamic lift.

31. 



The greater the curvature of the streamline, the greater
the decrease in velocity.
The streamline curvature above the aerofoil can be
increased by increasing the angle of attack (the angle at
which the aerofoil meets the streamline)
However, if the angle of attack is too large, the
streamlines about the aerofoil could converge and
dissipate. This diminishes the lift, an event known as stall.
Aircraft wings can deploy slats and flaps to increase
surface area to give extra lift for take off or to increase
air resistance to provide additional drag for landing and
decelerating.

32. Slats
Flaps

33. Bernoulli’s water tower
Flow direction
As flow velocity increases, pressure at base of tube
decreases from left to right

34. Venturi nozzle
Venturi nozzle
Venturi nozzle causes great increase in flow velocity, hence great decrease in pressure

35. 
Observations of Bernoulli’s Principle






Wings of airplane
Sail of a boat
Hydrofoils of boat
Insecticide dispenser
Mesocyclone
Whirlpools