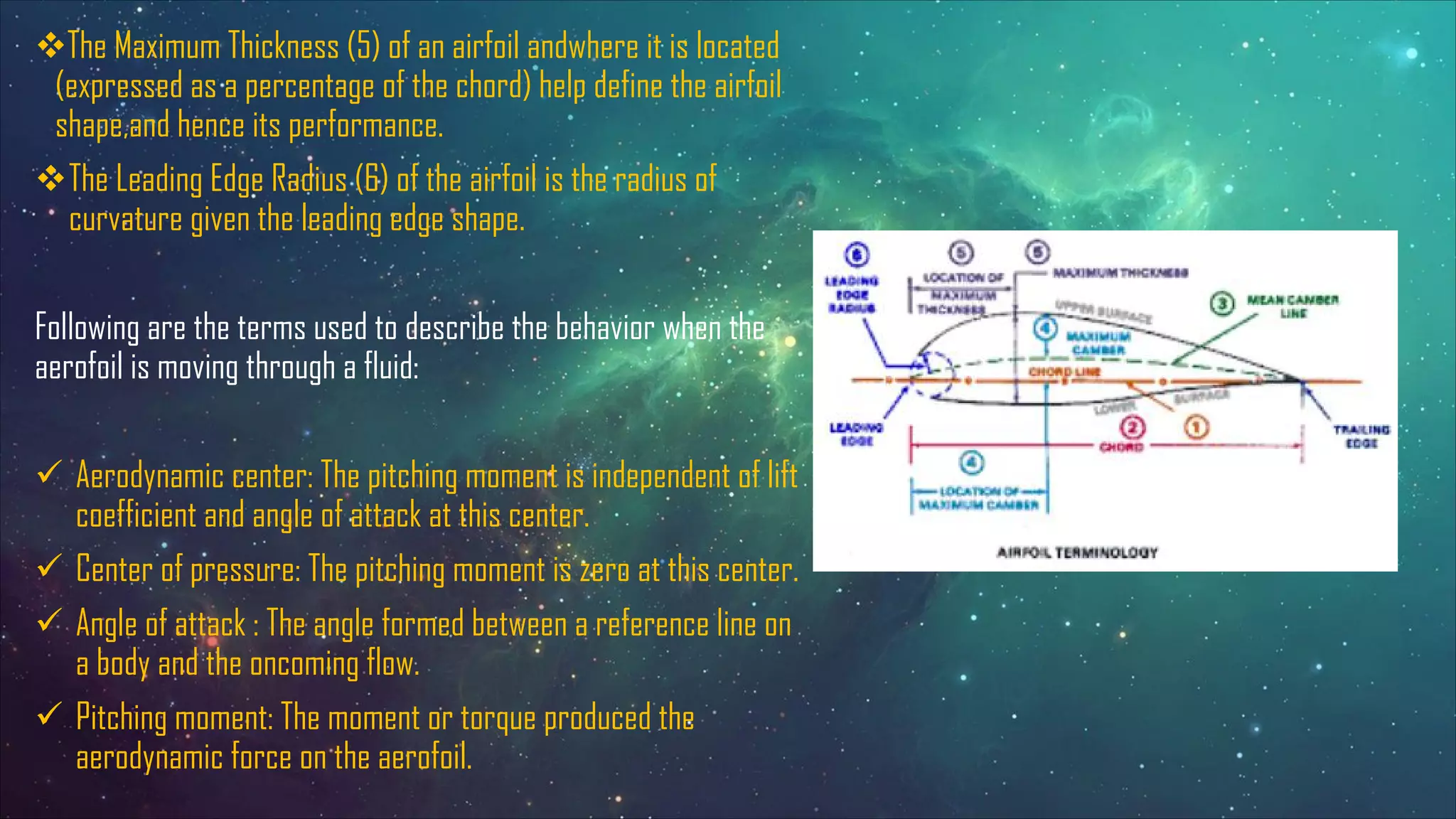
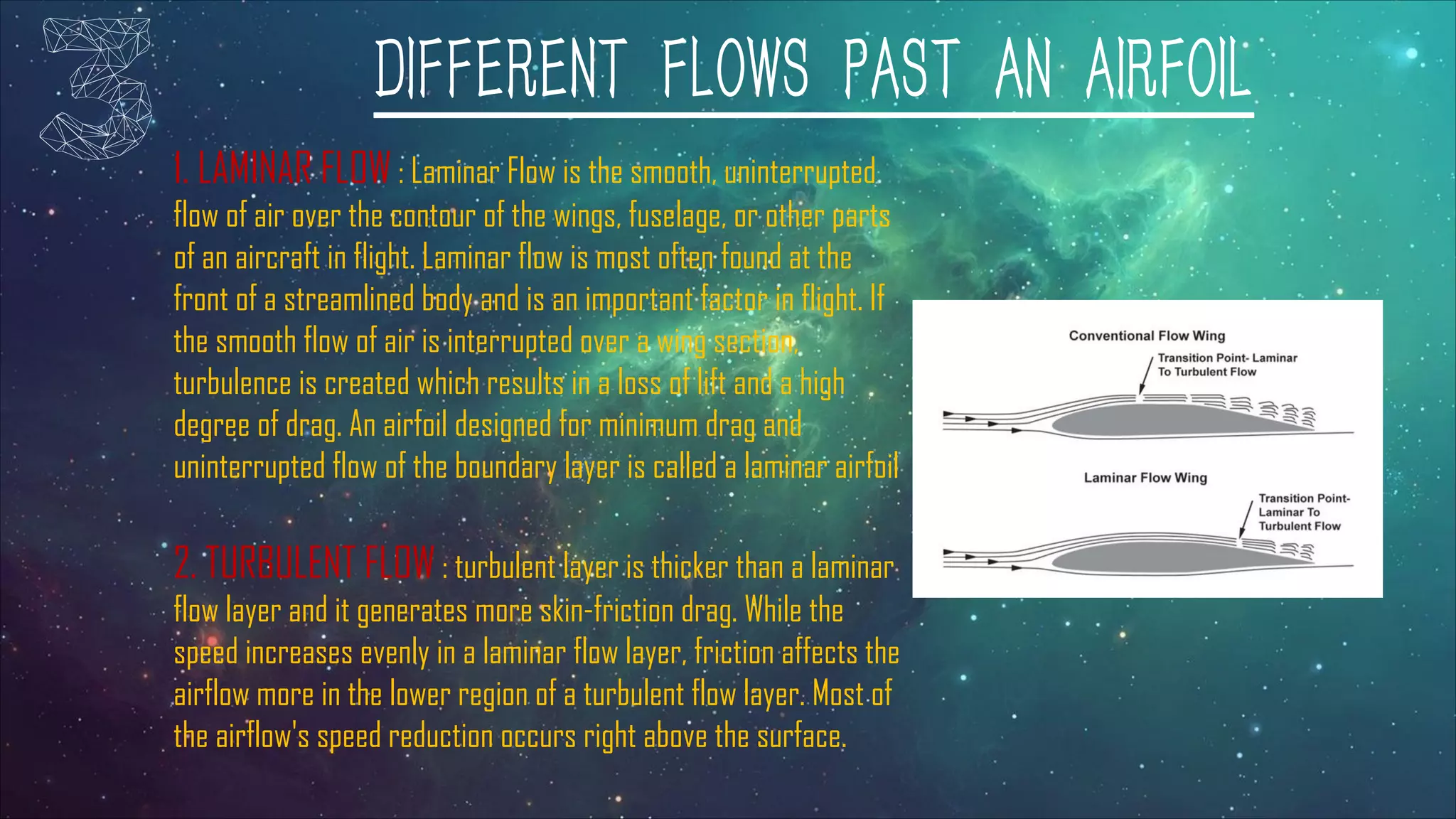
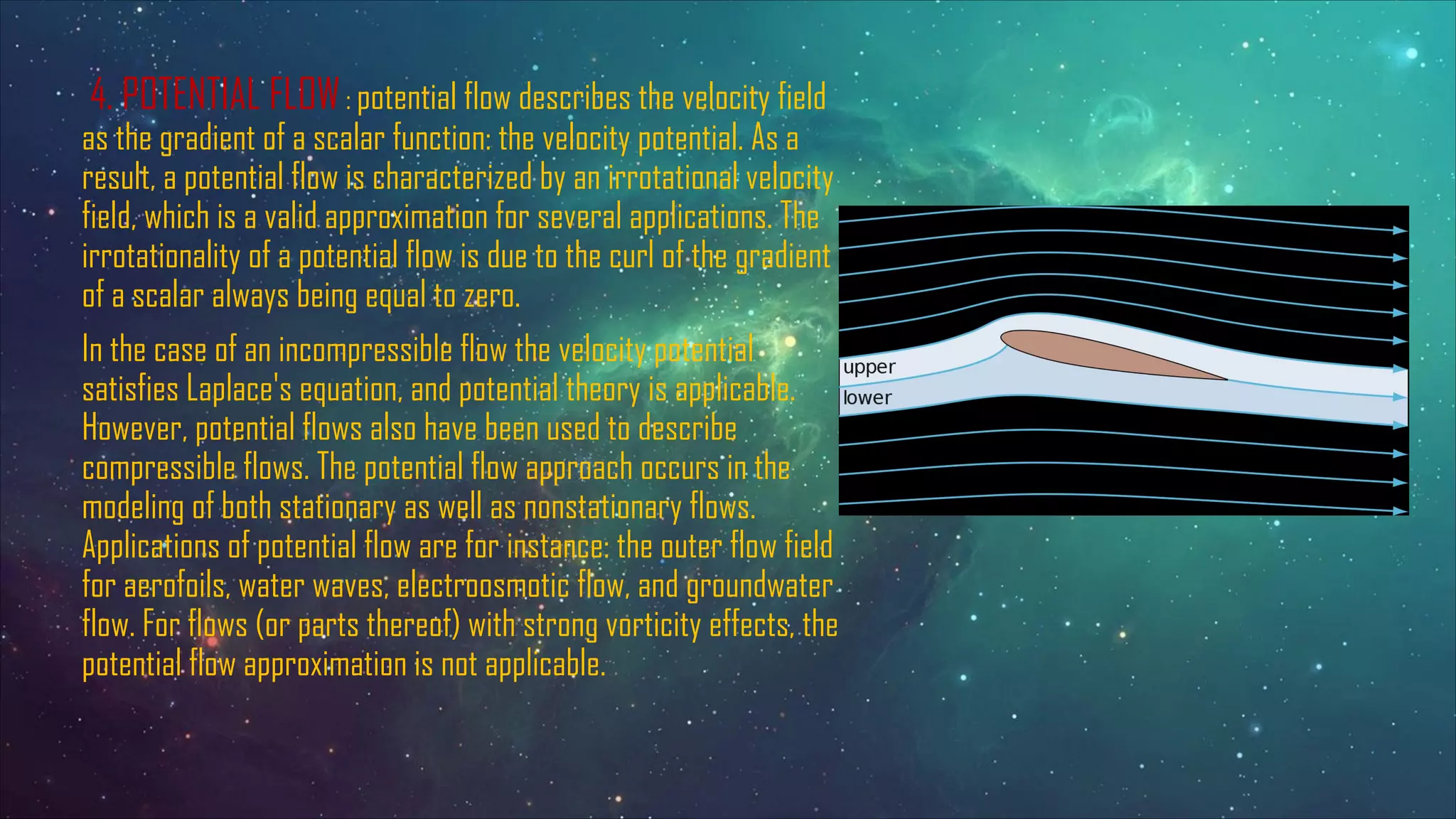
The document discusses the aerodynamics of airfoils, detailing their definitions, terminologies, types, and the principles of lift and drag. It explains the significance of flow characteristics such as laminar, turbulent, viscous, and potential flow in aerodynamics, along with the Kutta-Joukowski theorem for analyzing circulation and lift. Additionally, it highlights the role of viscosity in fluid behavior around airfoils, emphasizing the importance of maintaining smooth airflow for optimal performance.

1. FLOW PAST
AIRFOIL
SUBMITTED BY - K G PRIYANKA ,
1827023 , M8

2. 1 INTRODUCTION 2 AIRFOIL TERMINOLOGIES AND TYPE
3 DIFFERENT FLOWS PAST AN
AIRFOIL
4 FLOW AROUND AN AIRFOIL
CONTENTS

3. INTRODUCTION
Aerofoil or airfoil is defined as the cross-sectional shape that is designed with curved surface
giving it the most favorable ratio between lift and drag in flight. Lift is the component such that
the force is perpendicular to the direction of motion and drag is the component parallel to the
direction of motion. A similar idea is used in the designing of hydrofoils which is used when water
is used as the working fluid. .
The lift on an airfoil is primarily the result of its angle of attack. When oriented at a suitable angle,
the airfoil deflects the oncoming air (for fixed-wing aircraft, a downward force), resulting in a
force on the airfoil in the direction opposite to the deflection. This force is known as aerodynamic
force and can be resolved into two components: lift and drag. This pressure difference is
accompanied by a velocity difference, via Bernoulli's principle, so the resulting flowfield about the
airfoil has a higher average velocity on the upper surface than on the lower surface. The lift
force can be related directly to the average top/bottom velocity difference without computing
the pressure by using the concept of circulation and the Kutta–Joukowski theorem

4. AIRFOIL TERMINOLOGIES AND TYPES
1. AIRFOIL TERMONOLIGIES
v The Chord Line (1) is a straight line connecting the leading and trailing edges of the airfoil.
vThe Chord (2) is the length of the chordline from leading edge to trailing edge and is the
characteristic longitudinal dimension of an airfoil.
vThe Mean Camber Line (3) is a line drawn halfway between the upper and lower surfaces. The
chord line connects the ends of the mean camber line. The shape of the mean camber is
important in determining the aerodynamic characteristics of an airfoil section.
vMaximum Camber (4) (displacement of the mean camber line from the chord line) and where
it is located (expressed as fractions or percentages of the basic chord) help to define the
shape of the mean camber line.

5. vThe Maximum Thickness (5) of an airfoil andwhere it is located
(expressed as a percentage of the chord) help define the airfoil
shape,and hence its performance.
vThe Leading Edge Radius (6) of the airfoil is the radius of
curvature given the leading edge shape.
Following are the terms used to describe the behavior when the
aerofoil is moving through a fluid:
ü Aerodynamic center: The pitching moment is independent of lift
coefficient and angle of attack at this center.
ü Center of pressure: The pitching moment is zero at this center.
ü Angle of attack : The angle formed between a reference line on
a body and the oncoming flow.
ü Pitching moment: The moment or torque produced the
aerodynamic force on the aerofoil.

6. 2. AIRFOIL TYPES
Ø SYMMETRIC AIRFOIL -Symmetric airfoils are those which have the same
shape below and above the cord line. The opposite of symmetric airfoil
would be a cambered airfoil. The aerodynamic force is generated by
the relative motion of the body with respect to the mediumA
symmetrical airfoil will generate zero lift at zero angle of attack. But
as the angle of attack increases, the air is deflected through a larger
angle and the vertical component of the airstream velocity increases,
resulting in more lift.
Ø CAMBER AIRFOIL - Camber is the asymmetry between the two acting
surfaces of an airfoil, with the top surface of a wing (or
correspondingly the front surface of a propeller blade) commonly
being more convex (positive camber).Camber is usually designed into
an airfoil to maximize its lift coefficient. This minimizes the stalling
speed of aircraft using the airfoil. An aircraft with cambered wings will
have a lower stalling speed than an aircraft with a similar wing loading
and symmetric airfoil wings.

7. DIFFERENT FLOWS PAST AN AIRFOIL
1. LAMINAR FLOW : Laminar Flow is the smooth, uninterrupted
flow of air over the contour of the wings, fuselage, or other parts
of an aircraft in flight. Laminar flow is most often found at the
front of a streamlined body and is an important factor in flight. If
the smooth flow of air is interrupted over a wing section,
turbulence is created which results in a loss of lift and a high
degree of drag. An airfoil designed for minimum drag and
uninterrupted flow of the boundary layer is called a laminar airfoil
2. TURBULENT FLOW : turbulent layer is thicker than a laminar
flow layer and it generates more skin-friction drag. While the
speed increases evenly in a laminar flow layer, friction affects the
airflow more in the lower region of a turbulent flow layer. Most of
the airflow's speed reduction occurs right above the surface.

8. It turns out that the air's velocity combined with the distance it has traveled across a
surface determine whether the boundary layer is laminar or turbulent. Engineers measure
this using a "Reynolds Number" - named after Osborne Reynolds, who popularized its use. A
low Reynolds number indicates laminar flow, and a high Reynolds number indicates
turbulent flow.
3. VISOCOUS FLOW :The viscosity of a fluid is a measurement of that fluid?s resistance to
shearing. Fluids behave in such a way that, unlike solids, it is not the amount of shear
placed upon the liquid but the rates at which that shear is applied that determines its
resistance to flow.
From the perspective of a small amount of fluid, flowing along with the greater stream of
fluid the following behaviors can be deduced. As the fluid particle passes over the surface,
viscous forces cause it to stick to the surface. Meanwhile, the rest of the flow continues on
its way, providing a shearing force to that particle.
A wing provides lift because the viscosity of air causes an acceleration in the flow of air as
it moves to equalize the pressure difference of the wake of the wing. Changing the direction
of the air as it flows over the wing brings about this acceleration, and therefore an increase
in velocity, and a decrease in pressure. Without this viscous force to change the direction
of the flow, it would be impossible to fly.

9. 4. POTENTIAL FLOW: potential flow describes the velocity field
as the gradient of a scalar function: the velocity potential. As a
result, a potential flow is characterized by an irrotational velocity
field, which is a valid approximation for several applications. The
irrotationality of a potential flow is due to the curl of the gradient
of a scalar always being equal to zero.
In the case of an incompressible flow the velocity potential
satisfies Laplace's equation, and potential theory is applicable.
However, potential flows also have been used to describe
compressible flows. The potential flow approach occurs in the
modeling of both stationary as well as nonstationary flows.
Applications of potential flow are for instance: the outer flow field
for aerofoils, water waves, electroosmotic flow, and groundwater
flow. For flows (or parts thereof) with strong vorticity effects, the
potential flow approximation is not applicable.

10. FLOW AROUND AN AIRFOIL
The Kutta-Joukowski theorem shows that lift is proportional to circulation, but apparently the value of
the circulation can be assigned arbitrarily.
The solution of flow around a cylinder tells us that we should expect to find two stagnation points
along the airfoil the position of which is determined by the circulation around the profile. There is a
particular value of the circulation that moves the rear stagnation point (V=0) exactly on the trailing
edge.
This condition, which fixes a value of the circulation by simple geometrical considerations is the Kutta
condition.
Using Kutta condition the circulation is not anymore a free variable and it is possible to evaluate the
lift of an airfoil using the same techniques that were described for the cylinder. Note that the flow
fields obtained for a fixed value of the circulation are all valid solutions of the flow around an airfoil.
The Kutta condition chooses one of these fields, one which represents the best actual flow.

11. We can try to give a feasible physical justification of the Kutta
condition; to do this we need to introduce a concept that is
ignored by the theory for irrotational inviscid flow: the role
played by the viscosity of a real fluid.
Suppose we start from a static situation and give a small
velocity to the fluid. If the fluid is initially at rest it is also
irrotational and, neglecting the effect of viscosity, it must
remain irrotational due to Thompson theorem.
The flow field around the wing will then have zero circulation,
with two stagnation points located one on the lower face of
the wing, close to the leading edge, and one on the upper face,
close to the trailing edge.

12. A very unlikely situation is created at the trailing edge: a fluid particle on the lower side
of the airfoil should travel along the profile, make a sharp U-turn at the trailing edge, go
upstream on the upper face until it reaches the stagnation point and then, eventually,
leave the profile. A real fluid cannot behave in this way. Viscosity acts to damp the sharp
velocity gradient along the profile causing a separation of the boundary layer and a wake
is created with shedding of clockwise vorticity from the trailing edge.
Since the circulation along a curve that includes both the vortex and the airfoil must still
be zero, this leads to a counterclockwise circulation around the profile. But if a nonzero
circulation is present around the profile, the stagnation points would move and in
particular the rear stagnation point would move towards the trailing edge. The sequence
vortex shedding -> increase of circulation around the airfoil -> downstream migration of
the rear stagnation point continues until the stagnation point reaches the trailing edge.
When this happens the sharp velocity gradient disappears and the vorticity shedding
stops. This ``equilibrium'' situation freezes the value of the circulation around the airfoil,
which would not change anymore.

13. SIGNING OFF - K G PRIYANKA , 1827023 ,M8