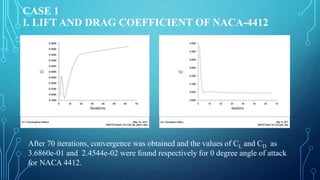
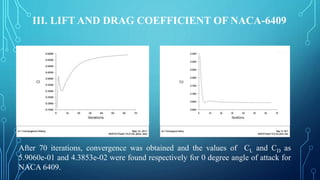
The document presents a computational fluid dynamics analysis of flow over NACA airfoils using ANSYS Fluent. It describes modeling NACA-4412, NACA-6409, and NACA-0012 airfoils, applying boundary conditions, and analyzing lift, drag, velocity and pressure distributions. The analysis found that NACA-4412 had a higher lift-to-drag ratio than NACA-6409. Additionally, increasing the angle of attack was found to initially increase lift and drag coefficients until a certain point, after which lift decreased while drag continued increasing.

1. FLOW ANALYSIS OVER NACAAIRFOILS
USING FLUENT
PRESENTED BY:
AMIYA KUMAR SAMAL - 1301109115
MECHANICAL ENGINEERING
PARALA MAHARAJA ENGG. COLLEGE
8TH SEMESTER
GUIDED BY :
MR. KASHINATH DHAMUDIA (ASST. PROFESSOR)

2. CONTENTS
INTRODUCTION
AIRFOIL TERMINOLOGY
SHEMATIC VIEW OF AIRFOIL
NACAAIRFOIL
OBJECTIVE
RESEARCH METHODOLOGY
GOVERNING EQUATIONS
MODELLING AND MESHING
FLUENT ANALYSIS
BOUNDARY CONDITION
COMPARATIVE CASE STUDY
CALCULATION
RESULTS
CONCLUSIONS
REFERENCES

3.  INTRODUCTION
 Aerodynamics
Aerodynamic force: Lift and Drag
 Computational fluid dynamics (CFD)
 Airfoil

4.  AIRFOIL TERMINOLOGY
 Chord Line
 Leading Edge
 Trailing Edge
 Angle of Attack
 Upper Surface
 Lower Surface
 Camber Line

5.  SCHEMATIC VIEW OF AIRFOIL

6.  NACAAIRFOIL
 The NACA airfoils are airfoil shapes for aircraft wings developed by
the National Advisory Committee for Aeronautics (NACA).
 The shape of the NACA airfoils is described using a series of digits
following the word "NACA".
NACA 4-digit series
 For example, the NACA 2412 airfoil has a maximum camber of 2% located
40% (0.4 chords) from the leading edge with a maximum thickness of 12%
of the chord.

7.  OBJECTIVE
 The objective of this project is to make a comparative study between
NACA-4412 & NACA-6409 and effect of angle of attack on NACA-0012
using ANSYS FLUENT.
 The parameters to be determined are flow characteristics such as velocity
distribution and pressure distribution .
 Determination of performance characteristics such as lift coefficient(CL) and
drag coefficient(CD).

8.  RESEARCH METHODOLOGY
LITERATURE SURVEY
PROBLEM DEFINITION
MODELING, MESHING AND APPLYING
BOUNDARY CONDITION IN ANSYS FLUENT
CARRYING OUT ANALYSIS IN FLUENT
OBTAINING THE RESULTS
CONCLUSION AND REPORT PREPARATION

9.  GOVERNING EQUATION
 Continuity equation:
𝝏𝝆
𝝏𝒕
+ 𝛁 . (𝝆𝑽) = 𝟎
 Momentum equations:
𝝏(𝝆𝒖)
𝝏𝒕
+ 𝛁 . 𝝆𝒖𝑽 = −
𝝏𝒑
𝝏𝒙
+ ρfx
𝝏(𝝆𝒗)
𝝏𝒕
+ 𝛁 . 𝝆𝒗𝑽 = −
𝝏𝒑
𝝏𝒚
+ ρfy
𝝏(𝝆𝒘)
𝝏𝒕
+ 𝛁 . 𝝆𝒘𝑽 = −
𝝏𝒑
𝝏𝒛
+ 𝝆fz

10. MODELING AND MESHING
 The modeling has been done in ANSYS workbench 15.
 NACA-4412,NACA-6409 and NACA-0012 airfoil profile was modeled by
exporting coordinate data.
 Meshing was done in ANSYS using a rectangular domain.

11.  MESHED AIRFOIL PROFILE

12.  FLUENT ANALYSIS
 Flow analysis is carried out by using CFD package FLUENT.
 Working parameter
I. Working Fluid - Air
II. Density of Working Fluid at inlet - 1.225kg/m
3
III. Viscosity of Working Fluid - 1.7894 ×10
-5
kg/m-s
IV. Pressure Velocity Coupling - SIMPLE
V. Meshing Scheme - Hexahedral

13.  BOUNDARY CONDITION
EDGE NAME TYPES OF BOUNDARY
A Inlet Velocity
B Outlet Pressure
C Top wall Stationary wall ,no slip
D Bottom wall Stationary wall ,no slip
A
C
D
B

14.  COMPARATIVE CASE STUDY FOR FLOW
ANALYSIS OVER NACA PROFILES
 CASE 1: A comparative flow analysis of NACA-6409 and NACA-4412
airfoil .
 CASE 2: Effect of angle of attack on lift coefficient and drag coefficient
on NACA-0012.

15.  CALCULATION
Re=
𝝆𝑽𝑫
µ
Assume, Reynolds No.(Re) =65000
For air,
Density(ρ) = 1.225kg/m3
Dynamic viscosity(µ) = 1.7894 ×10-5kg/m-s
Chord length(D) =1m
From relation,
Velocity(V) =0.9495 m/s

16. CASE 1
I. LIFT AND DRAG COEFFICIENT OF NACA-4412
After 70 iterations, convergence was obtained and the values of CL and CD as
3.6860e-01 and 2.4544e-02 were found respectively for 0 degree angle of attack
for NACA 4412.

17. II. VELOCITY AND PRESSURE DISTRIBUTION OF
NACA-4412
Velocity distribution over NACA 4412 aerofoil
for an angle of attack 0 degree.
Pressure distribution over NACA 4412 aerofoil for
an angle of attack 0 degree.

18. III. LIFT AND DRAG COEFFICIENT OF NACA-6409
After 70 iterations, convergence was obtained and the values of CL and CD as
5.9060e-01 and 4.3853e-02 were found respectively for 0 degree angle of attack for
NACA 6409.

19. IV. VELOCITY AND PRESSURE DISTRIBUTION OF
NACA-6409
Velocity distribution over NACA 6409 airfoil for
an angle of attack 0 degree
Pressure distribution over NACA 6409 airfoil
for an angle of attack 0 degree

20. V. COMPARISION OF COEFFICIENT OF LIFT AND
COEFFICIENT OF DRAG
AIRFOIL CL/CD
NACA-4412 15.017
NACA-6409 13.46

21. CASE 2
I. EFFECT OF ANGLE OF ATTACK
Effect of angle of attack on lift and pressure distribution

22. II. EFFECT OF ANGLE OF ATTACK ON LIFT AND
DRAG COEFFICIENT
Angle of Attack
Cd
&
Cl

23.  CONCLUSION
CASE1:
 Static pressure distribution on these two airfoils was visualized. It was found that for same
angle of attack, NACA 4412 has less negative pressure on the upper surface than NACA
6409.
 Coefficient of drag and coefficient of lift were found for different angle of attack from the
simulation.
 Finally, lift to drag ratio for these two airfoils were compared to find out the better airfoil. In
this case, NACA 4412 is better than NACA 6409.
CASE 2:
 If angle of attack increased, lift and drag coefficient could increase until certain angle. After
certain angle, the lift coefficient was decreasing whereas; drag coefficient increased.

24.  REFERENCES
 www.google.co.in
 www.wikipedia.com
 www.youtube.com
 www.slideshare.com
 www.lynda.com
 www.naca.com
 www.quroa.com
 ANSYS FLUENT 15, Tutorial Guide.
 International Journal of Research in Engineering and Technology
 International Journal of Mechanical Engineering project and Research
 Numerical and Experimental Investigation of the Flow Field around NACA Airfoil