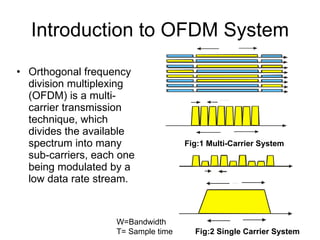
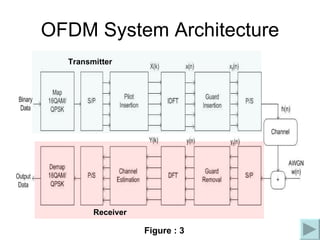
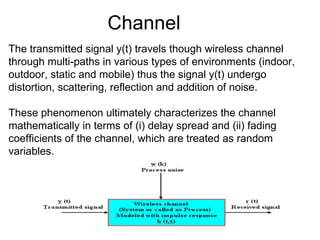
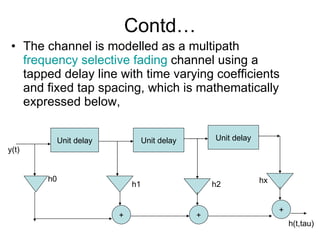
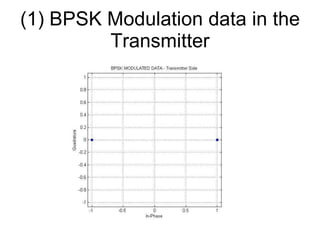
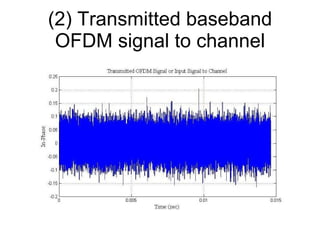
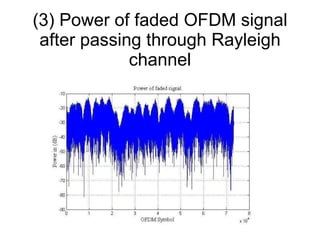
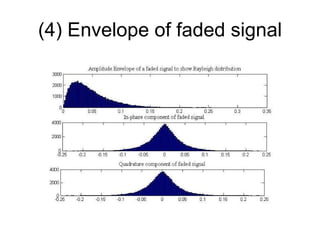
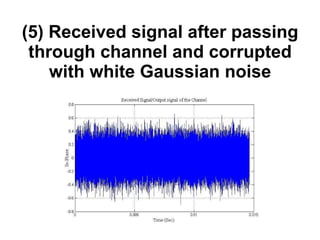
The document discusses channel modeling and Kalman filter-based estimation for OFDM wireless communication systems. It provides an introduction to OFDM systems and outlines the channel modeling process, including modeling the channel as a multipath frequency selective fading channel using a tapped delay line. It also discusses implementing channel estimation using a Kalman filter and presenting results on simulating OFDM signal transmission through a Rayleigh fading channel. The goal is to accurately estimate the channel fading parameters using a joint time-frequency domain estimation model.

1. Channel Modeling and Kalman Filter based Estimation of OFDM wireless Communication Systems M.Tech Progress seminar: Presented by: Barnali Dey

2. Outline Motivation Introduction to OFDM System Channel modeling Problem statement Channel Estimation – Kalman filter based Implementation Results Conclusions

3. Motivation The ultimate goal of wireless communication technology is to provide universal personal and multimedia communication irrespective of mobility and location with high data rates. When the data is transmitted at high data/bit rates over mobile radio channels then the channels may cause : Severe fading of transmitted signal when passed through channel Inter symbol interference (ISI) The focus of the future generation (4G) mobile system is on supporting higher data rates and providing seamless services across a multitude of wireless systems and networks. Orthogonal Frequency Division Multiplexing (OFDM) is one of the promising technique for 4G to mitigate ISI and fading in multi-path environment.

4. Introduction to OFDM System Orthogonal frequency division multiplexing (OFDM) is a multi-carrier transmission technique, which divides the available spectrum into many sub-carriers, each one being modulated by a low data rate stream. Fig:2 Single Carrier System Fig:1 Multi-Carrier System W=Bandwidth T= Sample time

5. OFDM System Architecture Figure : 3 Transmitter Receiver

6. Channel Modeling The purpose of channel modeling is to undertake the channel estimation problem. The channel modeling will be dealt step-by- step referring to Fig:3 . Fig.3 is divided into three major sections: Transmitter Channel Receiver

7. Transmitter Section First the high serial data rate input with sampling time T s is modulated using any digital modulation technique (BPSK, QAM, QPSK etc), to give digital symbols b m [k]. Next the modulated serial data is converted to low rate parallel data streams (M) using S/P converter. Due to this parallel conversion, the effective symbol duration is increased to T= MT s Where index k=I,2,….. is the symbol interval and m=0,1,….M-1 are the number of sub-channels.

8. … cont. Referring to Fig-3 the symbols b m [k] are modulated onto different sub-carriers using IFFT block, which is mathematically expressed as y(t)=∑ M-1 m=0 b m [k]exp(j2 π mt/T), for kT ≤ t ≤ (k+1)T -----(1) y(t) indicates modulated multiplexed signal that will be transmitted by OFDM transmitter.

9. … cont Due to the presence of complex exponential term in (1),the signal y(t) is orthogonal between different frequency sub-carriers

10. … To mitigate the effect of ISI, signal y(t) in (1) is added with a cyclic prefix thus the mathematical expression of y(t) becomes y(t)=∑ M-1 m=0 b m [k]exp(j2 π mt/T), for - Ψ +kT ≤ t ≤ (k+1)T --------------(2) where Ψ is guard interval.

11. Channel The transmitted signal y(t) travels though wireless channel through multi-paths in various types of environments (indoor, outdoor, static and mobile) thus the signal y(t) undergo distortion, scattering, reflection and addition of noise. These phenomenon ultimately characterizes the channel mathematically in terms of (i) delay spread and (ii) fading coefficients of the channel, which are treated as random variables.

12. Contd… The channel is modelled as a multipath frequency selective fading channel using a tapped delay line with time varying coefficients and fixed tap spacing, which is mathematically expressed below, Unit delay Unit delay Unit delay + + + h0 h1 h2 hx y(t) h(t,tau)

13. Contd… (3)

14. Channel model The channel considered in the present work is a Rayleigh with Jakes Doppler spectrum (in order to consider the mobility of either or both the transmitter and the receiver). The channel impulse response h l (t) is considered as WSSUS (Wide sense stationary uncorrelated scaterring) process. The WSSUS assumption of the channel means that the mean and the covariance (statistical properties of the channel) do not vary with respect to time.

15. … contd As the channel model h l (t) is stochastic in nature thus one has to express the correlation function of h l (t) which is expressed as E{h l (t) h l * (t- Δ t) }= Φ h ( Δ t)= σ l 2 Φ t ( Δ t) (4) where, σ l 2 is the variance of the channel fading at the l th path, which can be determined from the PDP of the considered channel. Statistically the variance of all the path should add upto 1. ∑ l=0 x σ l 2 =1

16. Receiver The received signal r(t) in the k th symbol duration is expressed as r(t)=∑ l=0 x h l (t)y(t-tau l )+n(t) (5) where n(t) is the noise term. Referring to Fig.(3) CP removal is carried out from the received signal first. After CP removal the signal is demodulated using FFT, which converts the time domain signal to frequency domain signal.

17. … contd The output of the demodulator block is called the measured signal, ‘ S k,q ‘. Where k= kth symbol interval, k=1.2.3…. q = number of sub-carriers generated by IFFT/FFT operation This signal is actually the input to the estimator block.(which is the Kalman Filter) The impulse response h l (t) is assumed to be quasi-static at k th symbol instant, thus h(t)=h(kT) for kT ≤ t ≤ (k+1)T

18. … .contd The q th sub-carrier output of s k,q from the demod. Is expressed as, s k,q =c k,q H k,q +v k,q (6) where, H k,q characterizes the channel fading and c k,q =1.

19. Simulation Parameter for OFDM Transmission System operates with 5MHz bandwidth Sub-channels/sub-carriers=256 Total symbol period=57µsec CP period= 6µsec (30 samples) One OFDM symbol=286 symbols Ts=1/BW=sampling time Δ f=BW/sub-carrier=BW/256=19.53KHz=frequency spacing of sub-carrier Carrier frequency=2.4GHz Two multipaths Rayleigh channel Delays=0, Ts Normalised Doppler frequency (fd*Ts)=0.05 Pilot insertion rate 1:8

20. Simulation Results of OFDM signal generated, transmitted and received when passing through a Rayleigh fading channel

21. (1) BPSK Modulation data in the Transmitter

22. (2) Transmitted baseband OFDM signal to channel

23. (3) Power of faded OFDM signal after passing through Rayleigh channel

24. (4) Envelope of faded signal

25. (5) Received signal after passing through channel and corrupted with white Gaussian noise

26. Channel characterization and modeling The channel considered in the present work is a Rayleigh with Jakes Doppler spectrum (in order to consider the mobility of either or both the transmitter and the receiver). Also the channel impulse response is considered as WSSUS. (a) Theoritical Rayleigh Jakes model: Let the continuous time channel model of l th scatterer and m th carrier is represented as:

27. … .contd

28. … contd

30. Channel model as AR process The discreet time fading channel model can be approximated by AR process where {ai}= AR model parameter U m (n)= gaussian driving process with variance σ u 2.

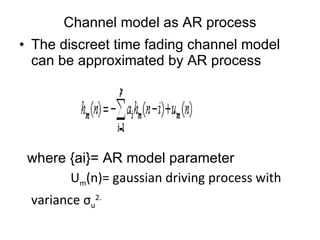
31. Determination of AR parameter The AR parameter are obtained by Yule-Walker equation: R hh θ= -r h Where R hh = fading channel ACF matrix of pxp θ = [ a 1, a 2 , ….a p ] T = px1 vector storing the AR parameter r h = px1 channel ACF vector

32. Also the varience of driving process noise can be found by : which gives the Power spectral density of AR(p) model

33. Problem Statement- Channel State Estimation The Channel Fading parameter H k,q needs to be estimated accurately given the output s k,q . For efficient Channel state estimation, a joint time-frequency domain channel estimation model will be developed in final stage of our work. Channel estimates are often achieved by multiplexing pilot symbols into data sequence and this technique is called Pilot Symbol Assisted Modulation (PSAM). Block Type All sub-carriers reserved for pilots wit a specific period Comb Type Some sub-carriers are reserved for pilots for each symbol 2-D Lattice type : Combination of above two.