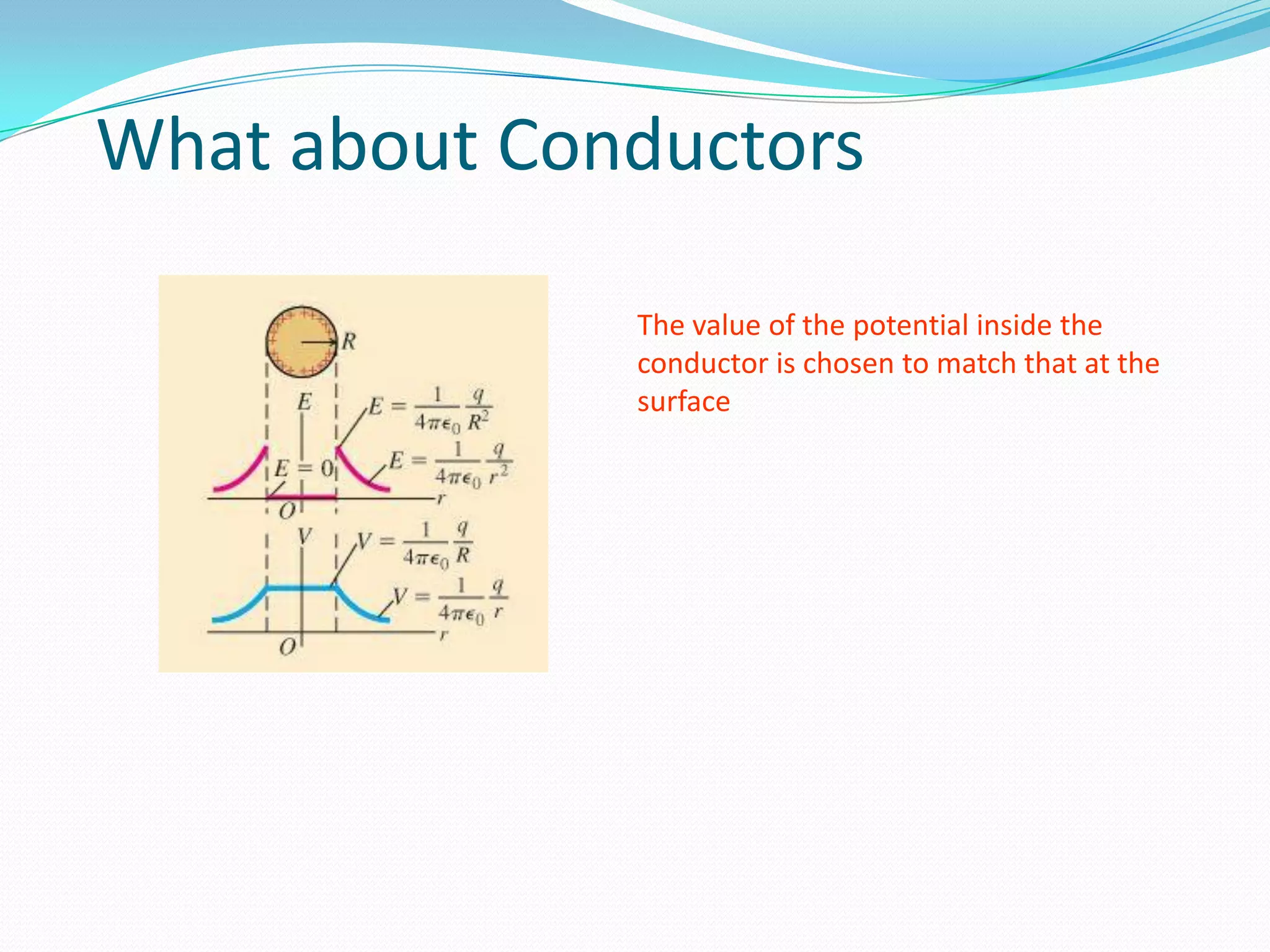
This document covers concepts in electromagnetic theory related to electrostatics, including electric potential, electric field, equipotential plots, dielectric polarization, Poisson's and Laplace's equations, boundary conditions, and capacitance. It defines key terms, shows examples of equipotential surfaces, discusses the relationship between electric field and potential, polarization in conductors and dielectrics, and how capacitance is calculated for simple capacitor geometries like parallel plates.

1. ELECTROMAGNETIC THEORY
(EE8391)
Ms.R.Dhanalakshmi , AP/EEE
Ms.P.Aileen Sonia Dhaas , AP/EEE

2. UNIT II ELECTROSTATICS
Electric potential – Electric field and
equipotential plots, Uniform and Non-Uniform field,
Utilization factor – Electric field in free space,
conductors, dielectrics – Dielectric polarization –
Dielectric strength – Electric field in multiple
dielectrics – Boundary conditions, Poisson’s and
Laplace’s equations, Capacitance, Energy density,
Applications.

3. ELECTRIC POTENTIAL

7. RELATIONSHIP BETWEEN E AND V

11. GENERAL CONSIDERATIONS

15. Equipotential Surfaces
Examples of equipotential surfaces
Point Charge Two Positive Charges

16. Equipotential Surfaces
 The electric field does no work as a charge is moved
along an equipotential surface
 Since no work is done, there is no force, qE, along
the direction of motion
 The electric field is perpendicular to the
equipotential surface

17. What about Conductors
 In a static situation, the surface of a conductor is an
equipotential surface
 But what is the potential inside the conductor if
there is a surface charge?
 We know that E = 0 inside the conductor
 This leads to
constant
or 
 V
dx
dV
0

18. What about Conductors
The value of the potential inside the
conductor is chosen to match that at the
surface

19. Dielectrics
Electrical field induced polarization

20. DIELECTRIC POLARIZATION
,
0 P
E
D




 
P: electric polarization field
For homogeneous material:
,
0 E
P e





,
0
0
0 E
E
E
P
E
D e










 




),
1
(
0 e


 

),
1
(
0
e
r 


 


Relative permittivity:
Electric susceptibility
Dielectric breakdown

21. Poisson’s and Laplace Equations
A useful approach to the calculation of electric potentials
Relates potential to the charge density.
The electric field is related to the charge density by the divergence
relationship
The electric field is related to the electric potential by a gradient relationship
Therefore the potential is related to the charge density by Poisson's equation
In a charge-free region of space, this becomes Laplace's equation

22. Electric Boundary Conditions
• On a perfect conductor
– The component of E parallel to the conducting surface is
zero
– The component of D normal to the conducting surface
is numerically equal to the charge density
– On a perfect dielectric material
– The component of E parallel to the interface is
continuous
– The component of D normal to the interface is
continuous

24. Perfect Dielectric Medium
 Tangential components of E are continuous
E1t = E2t
WATER DROPPLET
Medium 1 (air)
Medium 2

25. Perfect Dielectric Medium
 Normal components of E are discontinuous
ε1E1n = ε2E2n
WATER DROPPLET
Medium 1 (air)
Medium 2
no free charges

26. Perfect Conductor Medium
 Tangential components of E are zero
E1t = E2t = 0
WATER DROPPLET
Medium 1 (air)
Medium 2
Short circuit
X

27. Perfect Conductor Medium
 Normal components of E are discontinuous
E1n≠ 0
E2n= 0
WATER DROPPLET
Medium 1 (air)
Medium 2

28. Capacitance
• As shown above a capacitor consists of two conductors
separated by a non-conductive region.
– The non-conductive substance is called the dielectric
medium.
– The conductors contain equal and opposite charges on
their facing surfaces, and the dielectric contains an
electric field.
• A capacitor is assumed to be self-contained and
isolated, with no net electric charge and no influence
from an external electric field.

29. Capacitance
• An ideal capacitor is wholly
characterized by its capacitance C (in
Farads), defined as the ratio of charge
±Q on each conductor to the voltage V
between them
C = Q/V
• More generally, the capacitance is
defined in terms of incremental
changes
C = dq/dv

30. Parallel Plate Capacitor
• From Gauss’ Law the charge and the electric field
between the plates is related by
• Likewise, the line integral relating the potential and
the electric field simplifies to
• Thus the capacitance is given by