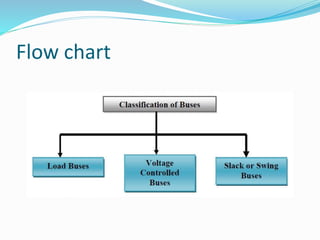
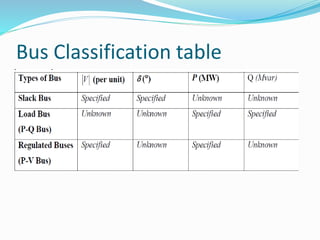
Load flow studies analyze power systems in steady state conditions, determining key parameters such as voltage, current, active, and reactive power. These studies are essential for designing, planning, and optimizing power system operations, with buses classified into load (pq), generator (p-v), and slack types based on specified and determined parameters. The load flow problem can be approached using static equations and bus admittance matrices, with assumptions for simplified calculations.

2. Introduction
 Load flow studies or Power flow studies is the analysis
of a power system in normal steady state condition.
 Load flow studies basically comprises of the
determination of
 Voltage
 Current
 Active Power
 Reactive Power

3. Importance
 Generation supplies demand(Load) plus losses.
 Bus voltage magnitude remain close to rated value.
 Generation operates within specified real and reactive
power limits.
 Transmission line and transformer are not overloaded.

4. Need of Load flow study
 Designing a power system.
 Planning a power system.
 Expansion of power system.
 Providing guide lines for optimum operation of power
system.
 Providing guide lines for various power system studies.

5. Bus Classification
 A bus is a node at which many Transmission lines, Loads
Generators are connected.
 It is not necessary that all of them be connected to every
bus.
 Bus is indicated by vertical line at which no. of
components are connected.
 In load flow study two out of four quantities specified
and other two quantities are to be determined by load
flow equation.
 Depending upon that bus are classified.

6. Flow chart

7. Load bus or PQ Bus
 A buss at which the Active power and reactive power
are specified.
 Magnitude(V) and phase angle(δ) of the voltage will
be calculated.
 This type of busses are most common, comprising
almost 80% of all the busses in given power system.

8. Generator bus or P-V bus
 A bus at which the magnitude(V) of the voltage and
active power(P) is defined.
 Reactive power(Q) and Phase angle(δ) are to be
determined through load flow equation.
 It is also known as P-V bus.
 This bus is always connected to generator.
 This type of bus is comprises about 10% of all the
buses in power system.

9. Slack Bus
 Voltage magnitude(V) and voltage phase angle(δ) are
specified and real(P) and reactive(Q) power are to be
obtained.
 Normally there is only one bus of this type is given in
power system.
 One generator bus is selected as the reference bus.
 In slack bus voltage angle and magnitude is normally
considered 1+j0 p.u.

10. Bus Classification table

11. Static method
 The following variables are associated with each bus:
 Magnitude of voltage(V)
 Phase angle of voltage(δ)
 Active power(P)
 Reactive power(Q)
 The load flow problem can solved with the help of
load flow equation(Static load flow equation).

12. Continue
 The bus admittance matrix is given by:
 In general the equation for bus-1 can be written as:
Y11V1+Y12V2+Y13V3=I1
 For bus-2 and bus-3 we can write:
Y21V1+Y22V2+Y23 V3=I2
Y31V1+Y32V2+Y33 V3=I3

13. Continue
 So Ii=∑ Yik Vk where i,k=1,2,…,n
So complex power is denoted as

14. Continue
 In polar form we can write
 The equation is written as:
 Real and reactive power expressed as:

15. Approximate method
 A simple and approximate solution can be made by
following assumption:
1. Small line resistance are neglected which means
active power loss in line is zero i.e. θik ~ 90 ˚
2. Voltage magnitude at various must be within limits.
3. Active and reactive generator power at different
buses must be within the limits.

16. Continue
4. Total power generation must be equal to load plus
losses.
5. The system stability consideration impose a limit on
maximum values with δ.
6. All buses other than slack bus are PV buses. i.e. voltage
magnitude at all the buses, Including the slack bus, are
specified.
7. The angle δi so small that (sin(δi))= δi.

17. Continue
 with the above assumption the above equation can be
written as: