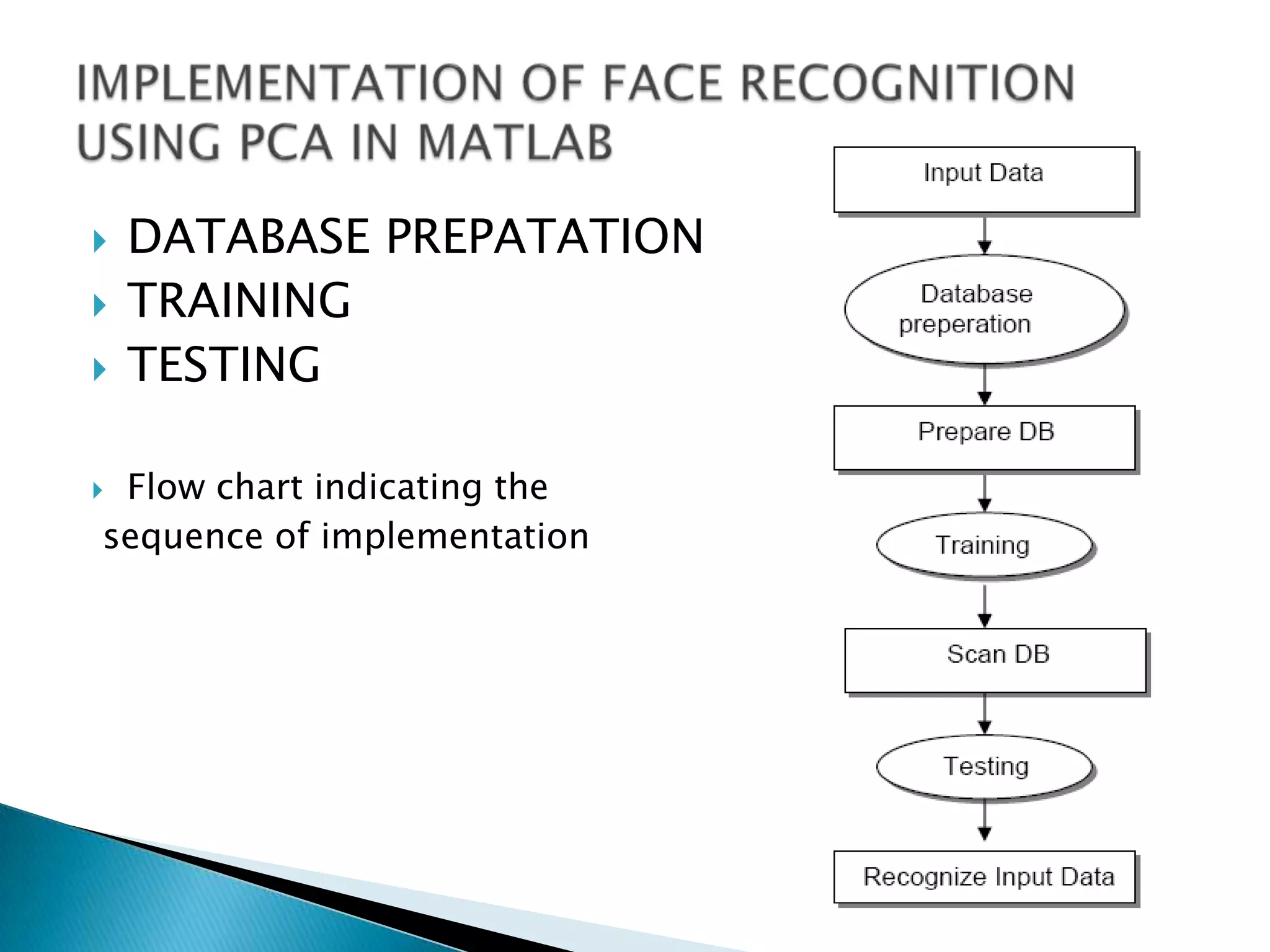
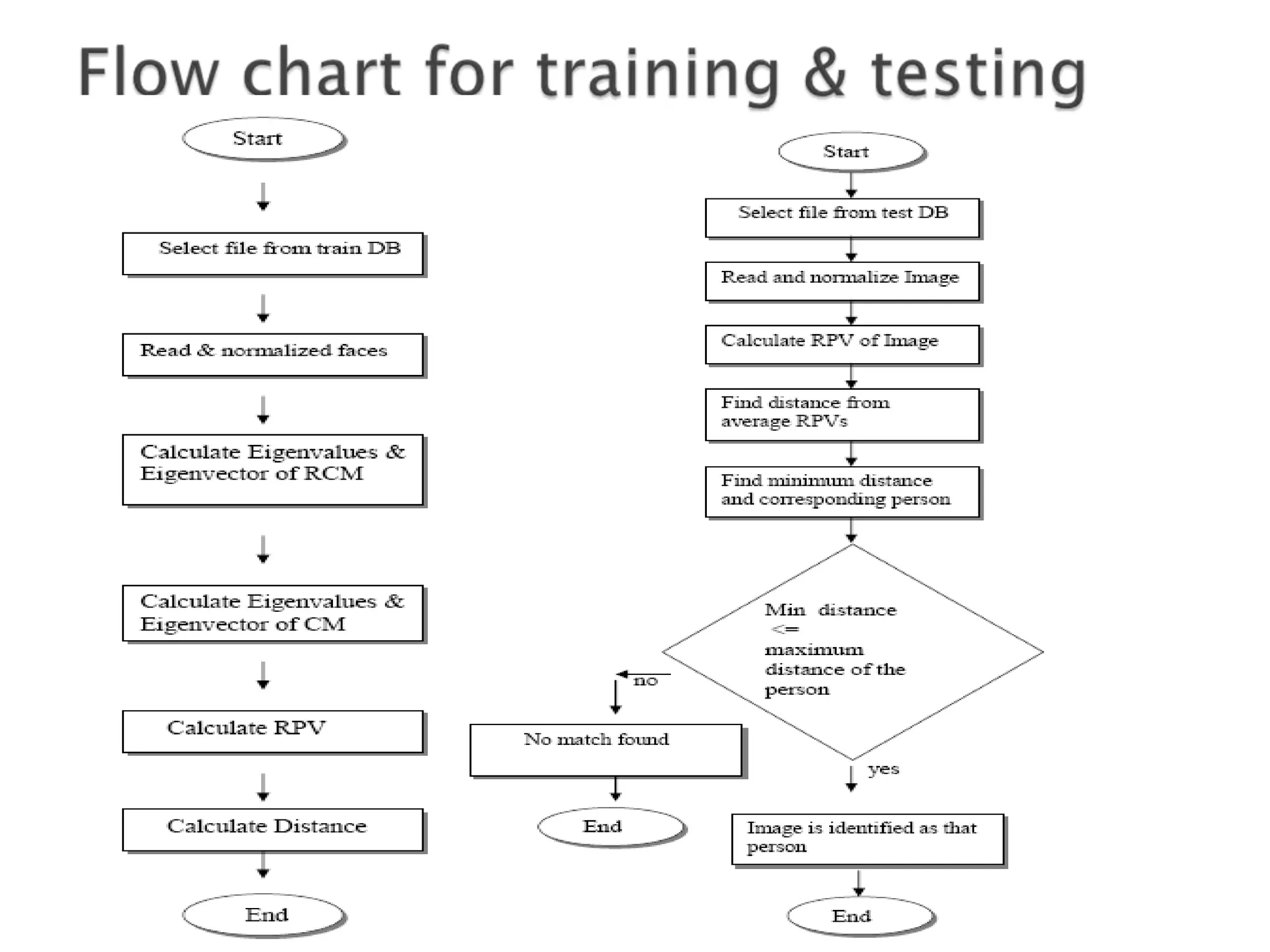
Face recognition uses principal component analysis (PCA) to reduce the dimensionality of face image data and identify patterns to recognize individuals. PCA involves extracting principal components from the data to summarize it with fewer variables while highlighting similarities and differences. The process involves getting sample face image data, subtracting the mean, calculating the covariance matrix, finding eigenvectors and eigenvalues to form a feature vector for projections of the data in the direction of the principal components. This allows for face recognition by training a database and testing unknown images.

1. Face recognition using principal
component analysis
by
ABHILASH KOTAWAR
VENKATA NARAYANA CHETTELA
KOMIRISHETTI SRAVAN

2.  In today's networked world, the need to maintain
the security of information is becoming both
increasingly important and increasingly difficult.
 BIOMETRICS represents a good compromise
between what’s socially acceptable and what’s
reliable, even when operating under controlled
conditions.
 Recently, technology became available to allow
verification of "true" individual identity. This
technology is based in a field called "biometrics".

4.  Face Recognition is the process of identification of
a person by their facial image. This technique
makes it possible to use the facial images of a
person to authenticate him into a secure
system, for criminal identification, for passport
verification,...
 Face recognition technology is the least intrusive
and fastest biometric technology.
 Face recognition systems unobtrusively take
pictures of people's faces as they enter a defined
area.
 This method is found to be fast, relatively
simple, and works well in a constrained
environment.

6.  PCA is a dimensionality reduction technique
based on extracting the desired number of
principal components of the multi-dimensional
data.
 PCA aims to:
 Summerise data with many independent
variables to a smaller set of derived variables.
 identifying patterns in data, and expressing the
data in such a way as to highlight
their similarities and differences.

7. Get some data:
x y
1.4000 1.6500
1.6000 1.9750
-1.4000 -1.7750
Mean=∑ Xi/n
-2.0000 -2.5250
-3.0000 -3.9500
2.4000 3.0750 variance=(∑(xi-avg)²)*1/(n-1)
1.5000 2.0250
2.3000 2.7500
sum of variances=16.3756
-3.2000 -4.0500
-4.1000 -4.8500
Average -0.4500 -0.5675
Variance 6.4228 9.9528

8.  For covariance we will use function
(∑(x-xbar)*(y-ybar)/(n-1)
X-Xbar Y-Ybar (X-Xbar)*(Y-Ybar)
1.8500 2.2175 4.1024
2.0500 2.5425 5.2121
-0.9500 -1.2075 1.1471
-1.5500 -1.9575 3.0341
-2.5500 -3.3825 8.6254
2.8500 3.6425 10.3811
1.9500 2.5925 5.0554
2.7500 3.3175 9.1231
-2.7500 -3.4825 9.5769
-3.6500 -3.4825 15.6311
7.9876 covariance

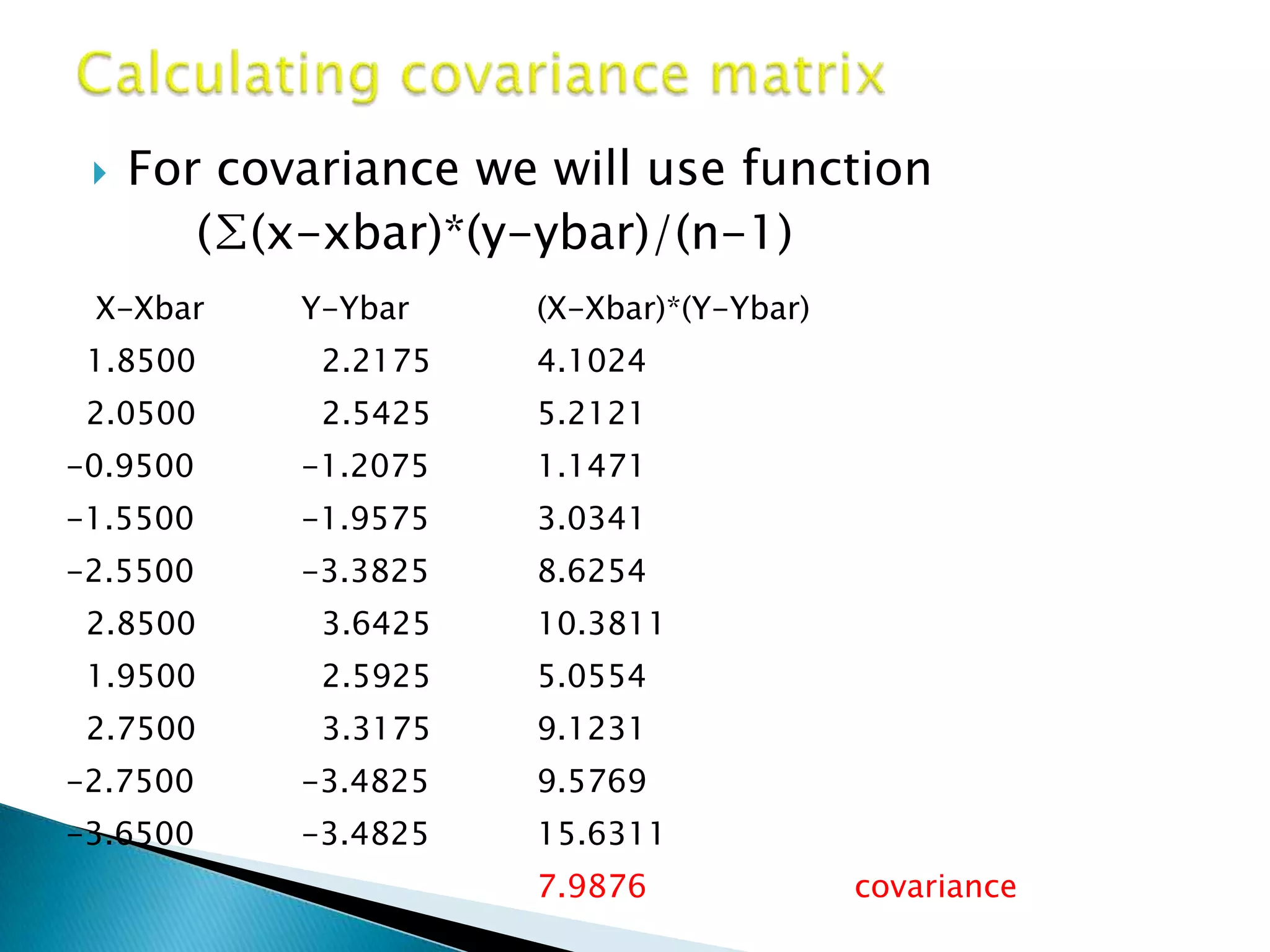
9.  In general the covariance matrix is
= [covariance(x,x) covariance(x,y)
covariance(y,x) covariance(y,y)]
= [variance(x) covariance(x,y)
covariance(x,y) variance(y)]
= [6.4228 7.9876
7.9876 9.9528]
 To obtain Eigen values by solving function
determinant {A-lamda(I)}=0
 Solving equation A, we get the Eigen values are
lamda=16.36809984,0.007462657
 Here sum of two eigen values is always equal to
the sum of variances

10.  To obtain Eigen vector by solving for matrix x in
such a way that, {A-lambda(i)}*[X]=[0].
 For first Eigen value 16.36809984, we get
[X]=[0.6262
0.7797]
 For second Eigen value 0.007462657,we get
[X]=[0.7797
-0.6262]
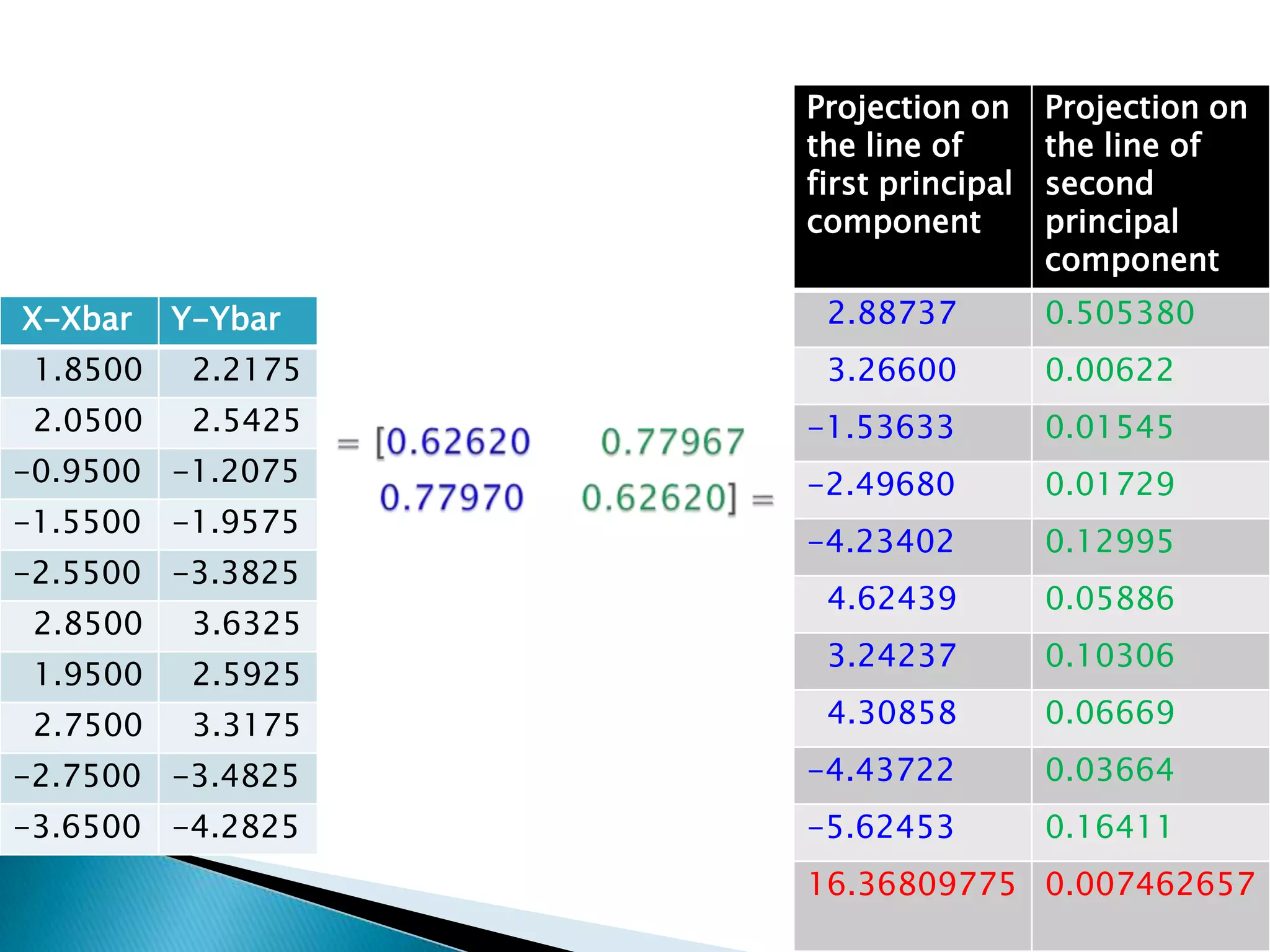
 To obtain coordinates of data point in the direction
of Eigen vectors by multiplying the centered data
matrix to the Eigen vector matrix

11. Projection on Projection on
the line of the line of
first principal second
component principal
component
X-Xbar Y-Ybar 2.88737 0.505380
1.8500 2.2175 3.26600 0.00622
2.0500 2.5425 -1.53633 0.01545
-0.9500 -1.2075 -2.49680 0.01729
-1.5500 -1.9575
-4.23402 0.12995
-2.5500 -3.3825
4.62439 0.05886
2.8500 3.6325
3.24237 0.10306
1.9500 2.5925
2.7500 3.3175 4.30858 0.06669
-2.7500 -3.4825 -4.43722 0.03664
-3.6500 -4.2825 -5.62453 0.16411
16.36809775 0.007462657

12. STEP1.Get some data
STEP2.subtract the mean
STEP3.Calculate the covariance matrix
STEP4.Calculate the Eigen vectors & Eigen values of
the covariance matrix
STEP5. choosing components and forming a feature
vector
 The variance of projections in the line of principal
component is equal to the Eigen values of the
principal components.
 First Eigen vector is able to explain around 99% of
total variance

13.  DATABASE PREPATATION
 TRAINING
 TESTING
Flow chart indicating the
sequence of implementation

15. 1.Acess control
 ATM
 AIRPORT A door lock control system
2.Entertainment:
 Video Game
 Human Computer Interaction
 Human Robotics

16. 3 Smart cards:
 Driver’s license
 Passports
 Voter registrations
 Pan card
4 Information Security:
 Desktop Logon
 Personal Driven Logon
 Database security
5 law Enforcement And Surveillance:
 Advanced video surveillance
 Drug trafficking
 And some other Commercial Applications:

17. HARD TO FOOL
 Face recognition is also very difficult to fool. It
works by comparing facial and marks -
specific proportions and angles of defined
facial features - which cannot easily be
concealed by beards, makeup.
 Byusing the facial recognition software, there's
no need for a picture ID, bankcard or personal
identification number (PIN) to verify a
customer's identity. This way business can
prevent fraud from occurring.

18. A face needs to be well lighted by
controlled light sources in
automated face authentication systems.
This is only a first challenge in a long list
of technical challenges that are
associated with
robust face authentication.
The risk involved with identity theft.

19.  Face recognition is a both challenging and
important recognition technique. Among all
the biometric techniques, face recognition
approach possesses one great advantage,
which is its user-friendliness.
 Face recognition promises latest security
invents in the upcoming trends based on bio-
metrics and pattern matching techniques and
algorithms.

20. CONCLUSION:

22.  The image may not always
be identified in facial
recognition alone.
 A picture is taken of a
patch of skin, & is then
broken up into smaller
blocks, Using algorithms.
 It can identify differences
between identical
twins, which is not yet
possible using facial
recognition software.
 Accurate identification can
increase by 20 to 25
percent.