This document appears to be an experiment report for a college-level electronics course. It includes: 1. Objectives to plot gain-frequency responses of passive band-pass and band-stop filters, determine their center frequencies and bandwidths, and how circuit resistance affects bandwidth. 2. Sample computations showing solutions to steps in the experiment involving passive filter circuit analysis. 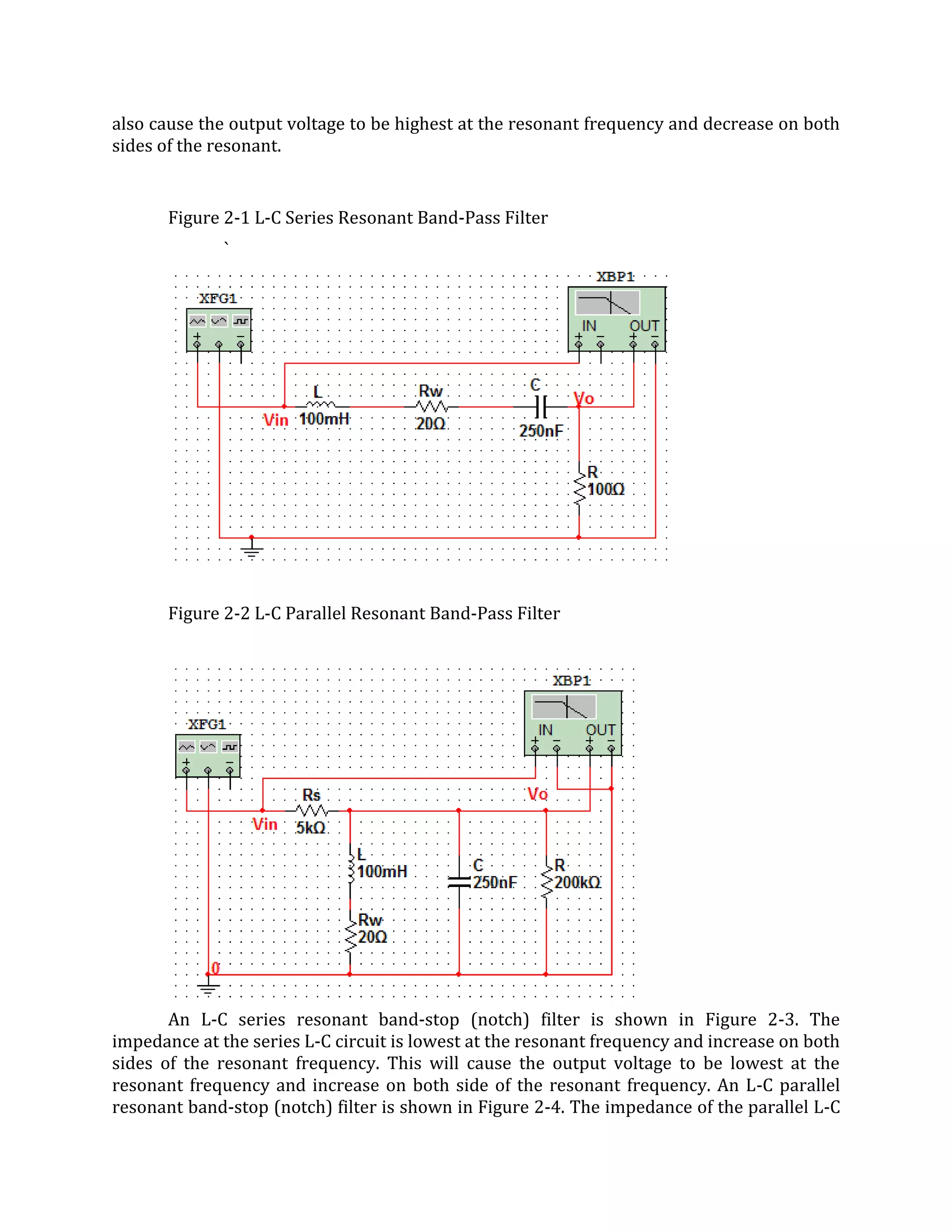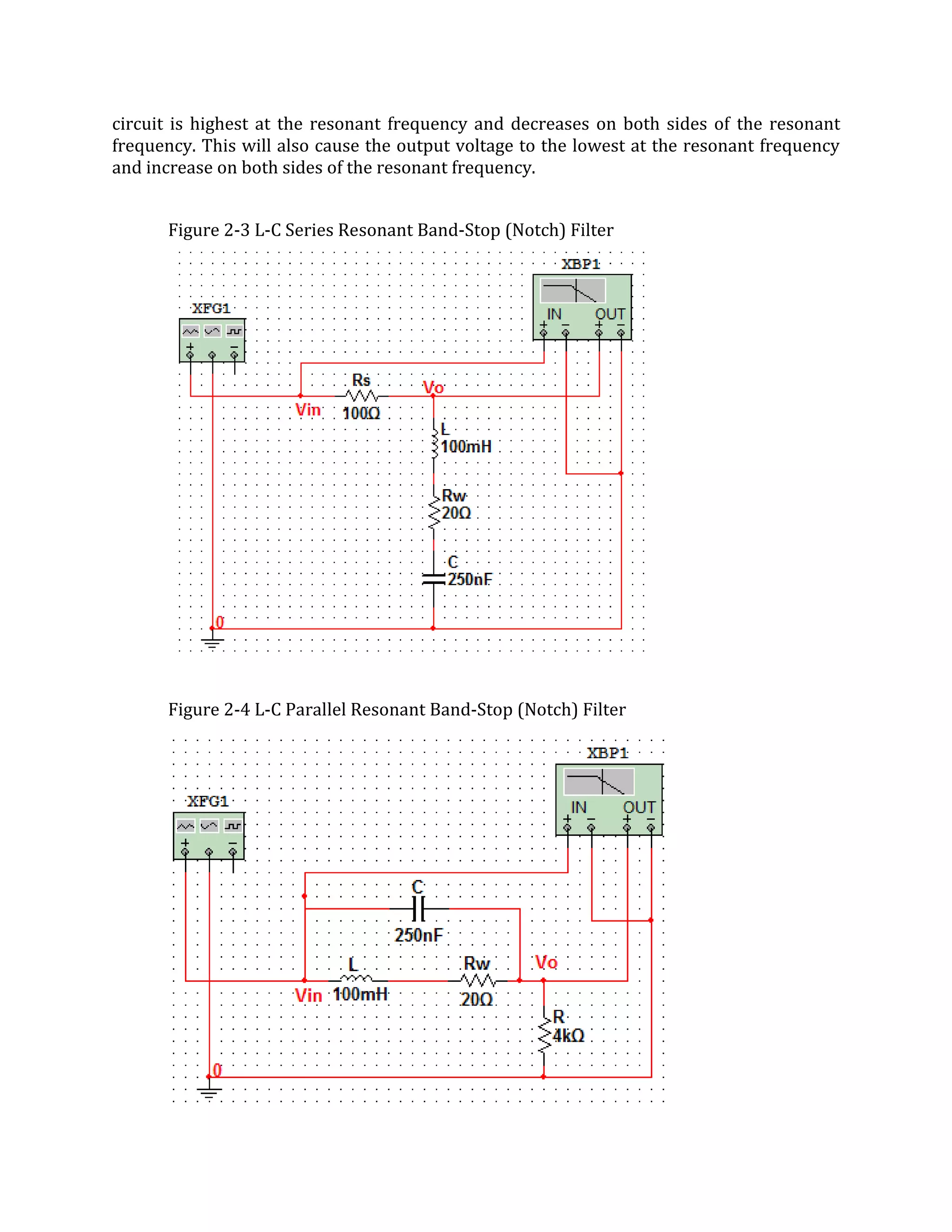3. A data sheet listing materials used and theoretical background on passive band-pass, band-stop, low-pass, and high-pass filters. It describes how to analyze L-C series and parallel resonant filters. 4. A procedure outlining steps to simulate band-pass and band-stop filters and analyze their responses

1. NATIONAL COLLEGE OF SCIENCE AND TECHNOLOGY
Amafel Bldg. Aguinaldo Highway Dasmariñas City, Cavite
EXPERIMENT # 2
Passive Band-Pass and Band-Stop Filter
Cauan, Sarah Krystelle P. July 05, 2011
Signal Spectra and Signal Processing/BSECE 41A1 Score:
Eng’r. Grace Ramones
Instructor

2. OBJECTIVES
1. Plot the gain-frequency response of an L-C series resonant and an L-C parallel
resonant band-pass filter.
2. Determine the center frequency and the bandwidth of the L-C band pass filter.
3. Determine how the circuit resistance affects the bandwidth of an L-C band-pass
filter.
4. Plot the gain-frequency response of an L-C series resonant and an L-C parallel
resonant band-stop (notch) filter.
5. Determine the center frequency and the bandwidth of the L-C band-stop filter.
6. Determine how the circuit resistance affects the bandwidth of an L-C band-stop
filter.

3. SAMPLE COMPUTATIONS
Solution for Step 4
Solution for Step 6:
Solution for Step 7
Solution for Question in Step 7
Solution for Step 8

5. Solution for Question in Step 8
Solution for Step 9
Solution for Step 10
Solution for Question in Step 10
Solution for Step 17

6. Solution for Step 19
Solution for Step 20
Solution for Question in Step 20
Solution for Step 21
Solution for Question in Step 21
Solution for Step 22
Solution for Step 23

7. Solution for Step 24
Solution for Step 25
Solution for Step 26
Solution for Question in Step 26
Solution for Step 33
Solution for Step 34

8. Solution for Question in Step 34
Solution for Step 35
Solution for Question in Step 35
Solution for Step 36
Solution for Step 37
Solution for Step 38

9. Solution for Step 43
Solution for Step 44
Solution for Question in Step 44
Solution for Step 45
Solution for Question in Step 45

10. Solution for Step 46
Solution for Step 47
Solution for Step 48
Solution for Step 49
Solution for Step 50
Solution for Step Question in 50

11. DATA SHEET
MATERIALS
One function generator
One dual-trace oscilloscope
Capacitors: one 0.1µF, one 0.25 µF
Inductors: one 50 mH, one 100 mH
Resistors: 100 Ω, 200 Ω, 2 kΩ, 4 kΩ, 5kΩ, 200kΩ
THEORY
In electronic communications systems, it is often necessary to separate a specific
range of frequency from the total frequency spectrum. This is normally accomplished with
filters. A filter is circuit that passes a specific range of frequencies while rejecting other
frequencies. A passive filter consists of passive circuit elements, such as capacitors,
inductors, and resistors. There are four basic types of filters, low-pass, high-pass, band-
pass, and band-stop. A low-pass filter is designed to pass all frequencies below the cutoff
frequency and reject all frequencies above the cutoff frequency. A high-pass filter is
designed to pass all frequencies above the cutoff frequency. A high-pass filter is designed to
pass all frequencies above the cutoff frequency and reject all frequencies below the cutoff
frequency. A band-pass filter passes all frequencies within a band of frequencies and rejects
all other frequencies outside the band. A band-stop filter rejects all frequencies within a
band of frequencies outside the band. A band-stop filter is often referred to as a notch filter.
In this experiment, you will study band-pass and band-stop (notch) filters.
The most common way to describe the frequency response characteristics of a filter
is to plot the filter voltage gain (Vo/Vi) in db as function of frequency (f). The frequency at
which the output power gain drops is 50% of the maximum value is called the cutoff
frequency (fC). When the output power gain drops to 50%, the voltage gain drops 3 db
(0.707 of the maximum value). When the filter dB voltage gain is plotted as a function of
frequency on semi log graph using straight lines to approximately the actual frequency
response, it is called a Bode plot. A bode plot is an ideal plot of filter frequency response
because it assumes that the voltage gain remains constant in the passband until the cutoff
frequency is reached, and then drops in straight line. The filter network voltage gain in dB
is calculated from the actual voltage gain (A) using the equation
AdB = 20 log A
Where A = Vo/Vi
An L-C series resonant band-pass filter is shown in Figure 2-1. The impedance of the
series L-C circuit is lowest at the resonant frequency and increases on both sides of the
resonant frequency. This will cause the output voltage to be highest at the resonant
frequency and decrease on both sides of the resonant frequency. At L-C parallel resonant
band-pas filter is shown in Figure 2-2. The impedance of the parallel L-C circuit is highest at
the resonant frequency and decreases on both sides of the resonant frequency. This will

12. also cause the output voltage to be highest at the resonant frequency and decrease on both
sides of the resonant.
Figure 2-1 L-C Series Resonant Band-Pass Filter
`
Figure 2-2 L-C Parallel Resonant Band-Pass Filter
An L-C series resonant band-stop (notch) filter is shown in Figure 2-3. The
impedance at the series L-C circuit is lowest at the resonant frequency and increase on both
sides of the resonant frequency. This will cause the output voltage to be lowest at the
resonant frequency and increase on both side of the resonant frequency. An L-C parallel
resonant band-stop (notch) filter is shown in Figure 2-4. The impedance of the parallel L-C

13. circuit is highest at the resonant frequency and decreases on both sides of the resonant
frequency. This will also cause the output voltage to the lowest at the resonant frequency
and increase on both sides of the resonant frequency.
Figure 2-3 L-C Series Resonant Band-Stop (Notch) Filter
Figure 2-4 L-C Parallel Resonant Band-Stop (Notch) Filter

14. The center frequency (fO) for the L-C series resonant and the L-C parallel resonant
band-pass and band-stop (notch) filter is equal to the resonant frequency of the L-C circuit,
which can be calculated from
For an L-C parallel resonant filter, the equation is accurate only for a high Q inductor
coil (Qf 10) where QL is calculated from
and XL is the inductive reactance at the resonant frequency (center frequency, fO)
and Rw is the inductor coil resistance.
In the band-pass and band-stop (notch) filters, the low-cutoff frequency (fC1) and the
high-cutoff frequency (fC2) on the gain-frequency plot are the frequencies where the whole
voltage gain has dropped 3dB (0.707) from the highest dB gain. The filter bandwidth (BW)
is the difference between the cutoff frequency (fC2) and the low-cutoff frequency (fC1)
Therefore,
BW = fC2 – fC1
The center frequency (f0) is the geometric mean of the low-cutoff frequency and the
high-cutoff frequency. Therefore,
The quality factor (Q) of the band-pass and the band-stop (notch) filters is the ratio
of the center frequency (fO) and the bandwidth (BW), and it is an indication of the activity
of the filter. Therefore,
A higher value of Q means a narrower bandwidth and a more selective filter.
The quality factor (QS) of a series resonant filter is determined by first calculating
the inductive reactance (XL) of the inductor at the resonant frequency (center frequency,
fO), and then dividing the inductive reactance by total series resistance (RT). Therefore,
Where

15. The quality factor (QP) of a parallel resonant filter is determined by first calculating
the inductive reactance (XL) of the inductor at the resonant frequency (center frequency,
fO), and then dividing the total parallel resistance (RP) by the inductive reactance (XL).
Therefore,
Because the inductor wire resistance (RW) is in series with inductor L, the circuits in
Figures 2-2 and 2-4 are not exactly parallel resonant circuits; the series combination of
inductance (L) and resistance (RW) must first be converted into an equivalent parallel
network with resistance REQ in parallel with inductance L. In Figure 2-2, the parallel
equivalent resistance (REQ) will also be in parallel with resistor r and resistor RS making the
total resistance of the parallel resonant circuit (RP), equal to the parallel equivalent of
resistors r, RS, and REQ. Therefore, RP can be solved from
In Figure 2-4, the parallel equivalent resistance (REQ) will be in parallel with resistor
R, making the total resistance of the parallel resonant circuit (RP) equal to the parallel
equivalent of resistor R and REQ. Therefore, RP can be solved from
The equation for converting resistance RW to the equivalent parallel resistance (REQ)
is
The parallel equivalent inductance LEQ is calculated from
This equivalent inductance can be considered equal to the original inductance (L)
for a high Q coil (QL 10)

16. PROCEDURE
Band-Pass Filters
Step 1 Open circuit file Fig 2-1. Make sure that the following Bode plotter settings are
selected. Magnitude, Vertical (Log, F=0 dB, I=–20dB), Horizontal (Log, F=2 kHz,
I=500Hz)
Step 2 Run the simulation. Notice that the voltage gain in db has been plotted between the
frequencies of 50Hz and 2Kz by the Bode plotter. Sketch the curve plot in the space
provided.
Question: Is the frequency response curve that of a band-pass filters? Explain why.
Yes. A band-pass is a filtering device that permits only the frequencies within a certain
band and rejects all other band. The plot curve shown above only allows the
frequencies from 501.697 Hz to 1.993 kHz.
Step 3 Move the cursor to the center of the curve at its peak point. Record the center
frequency (f0) and the voltage gain in dB on the curve plot.
fO= 996.84 Hz;
AdB= – 1.637 dB
Step 4 Based on the dB voltage gain, calculate the actual voltage gain (A) of the series
resonant band-pass filter at the center frequency.
A= 0.83

17. Step 5 Move the cursor as close as possible to a point on the left side of the curve that is 3
dB down from dB gain measured at frequency fO. Record the approximate
frequency (low-cutoff frequency, fC1) on the curve plot. Next, move the cursor as
close as possible to a point on the right side of the curve that is 3 dB down from the
dB gain measured at frequency fO. Record the approximate frequency (high-cutoff
frequency, fC2) on the curve plot.
fC1= 914.969 Hz
fC2= 1.104 kHz
Step 6 Based on the values of fC1 and fC2 measured on the curve plot, determine the
bandwidth (BW) of the series resonant band-pass filter.
BW= 189.031 Hz
Step 7 Based on the circuit component values in Figure 2-1, calculated the expected center
frequency (fO) of the series resonant band-pass filter.
fO(COMPONENT VALUE)= 1006.58 Hz
Question: How did the calculated value of the center frequency (fO) based on the circuit
component values compare with the measured value on the curve plot?
The calculated fO based on the circuit component values and the measured value is
almost equal. Their percentage difference is 0.97%.
Step 8 Based on the values of fC1 and fC2, calculate the center frequency (fO).
fO(fC1/fC2)= 1005.05 Hz
Question: How did the calculated value of the center frequency (fO) based on fC1 and fC2
compare with the measured value on the curve plot?
The percentage difference between the two is 0.82%.
Step 9 Based on the circuit component values, calculate the quality factor (QS) of the series
resonant band-pass filter.
QS= 5.27

18. Step 10 Based on the circuit quality factor (QS) and the center frequency (fO), calculate the
expected bandwidth (BW) of the series resonant band-pass filter.
BW(EXPECTED)= 191.00 Hz
Question: How did the expected bandwidth calculated from the value of QS and the center
frequency compare with the bandwidth measured on the curve plot?
The percentage difference between the two is 1.04%.
Step 11 Change the resistance of R to 200 Ω. Run the simulation again. Measure the center
frequency (fO) and the bandwidth (BW) from the curve plot and record the values.
fO=996.84 Hz
BW= 350.136 Hz
Questions: What effect did changing the resistance R have on the center frequency of the
series resonant band-pass filter? What effect did changing the resistance of R have on the
bandwidth of the series resonant band-pass filter? Explain.
The center frequency remain constant or did not change its value while the bandwidth
changed, it increased as the resistor increase. Therefore, the center frequency f O of a
series resonant band-pass filter is constant with change in the resistance R while the
bandwidth of the series resonant band-pass filter is directly proportional to the
resistance R.
Step 12 Change the capacitance of C to 0.1 µF. Run the simulation again. Measure the center
frequency (fO) and the bandwidth (BW) on the curve plot and record the values
Change the Bode plotter settings as needed.
fO=1.583 kHz
BW= 350 Hz

19. Questions: What effect did changing the capacitance of C have on the center frequency of
the series resonant band-pass filter? What effect did changing the capacitance of C have on
the bandwidth of the series resonant band-pass filter? Explain.
The bandwidth remains constant or did not change its value. The center frequency
however changed, it increased as the resistor increase. Therefore, the bandwidth of a
series resonant band-pass filter is affected by the change of capacitance C while the
center frequency of the series resonant band-pass filter is inversely proportional to the
capacitance C.
Step 13 Change the inductance of L to 50 mH. Run the simulation again. Measure the center
frequency (fO) and the bandwidth (BW) on the curve plot and record the values.
Change the Bode plotter settings as needed.
fO=1.423 kHz
BW= 386 Hz
Questions: What effect did the changing the inductance of L has on the center frequency of
the series resonant band-pass filter? What effect did changing the inductance of L have on
the bandwidth of the series resonant band-pass filter? Explain.
The center frequency and bandwidth was compared to the original circuit. By
changing the inductance, bandwidth BW and center frequency f O increased. Therefore,
bandwidth and the center frequency of the series resonant band-pass filter are
inversely proportional to the inductance of L

20. Step 14 Open circuit file Fig 2-2. Make sure that the following Bode plotter settings are
selected: Magnitude, Vertical (Log, F=0 dB, I=–20dB), Horizontal (Log, F=2 kHz,
I=500Hz)
Step 15 Run the simulation. Notice that the voltage gain in dB has been plotted between
the frequencies of 500 Hz and 2 kHz by the Bode plotter. Sketch the curve plot in
the space provided.
Question: Is the frequency response curve that of a band-pass filters? Explain why.
Yes. The curve plot above is a band-pass because it permits only the frequencies within
bandpass from 501.697 Hz to 1.993 kHz and rejects all other band.
Step 16 Move the cursor to the center of the curve at its peak. Record the center frequency
(fO) and the voltage gain in dB on the curve plot.
fO= 1.003 kHz
AdB= – 2.189 dB
Step 17 Based on the dB voltage gain, calculate the actual voltage gain (A) of the parallel
resonant band-pass filter at the center frequency.
A= 0.78
Step 18 Move the cursor at its close as possible to a point on the left side of the curve that is
3dB down from the dB gain measured at frequency fO. Record the approximate
frequency (low-cutoff frequency, fC1) on the curve plot. Next, move the cursor as
close as possible to a point on the right side of the curve that is 3 dB down from the

21. dB gain measured at frequency fO. Record the approximate frequency (high-cutoff
frequency fC2) on the curve plot.
fC1= 929.014 Hz
fC2= 1.093 kHz
Step 19 Based on the values of fC1 and fC2, determine the bandwidth (BW) of the parallel
resonant band-pass filter.
BW= 163.186 Hz
Step 20 Based on the circuit component values in Fig 2-2, calculate the expected center
frequency (fO) of the parallel resonant band-pass filter.
fO(COMPONENT VALUE)= 1006.58 Hz
Question: How did the calculated values of the center frequency (fO) base on the circuit
component values compare with measured values recorded on the curve plot?
The percentage difference between the calculated fO based on the circuit component
values and the measured value is only 0.37%.
Step 21 Based on the values of fC1 and fC2, calculate the center frequency (fO).
fO(fC1/fC2)= 1007.68 Hz
Question: How did the calculated value of the center frequency (fO) base on the fC1 and fC2
compare with the measured value on the curve plot?
The percentage difference between the two is 0.47%.
Step 22 Based on the value of L and RW, calculate the quality factor (QL) of the inductor.
QL=31.62
Step 23 Based on the quality factor (QL) of the inductor, calculate the equivalent parallel
inductor resistance (REQ) across the tank circuit.
REQ= 20016.488Ω

22. Step 24 Based on the value of REQ, RS, and R, calculate the total parallel resistance (RP)
across the tank circuit.
RP= 3922.20Ω
Step 25 Based on the value of RP, calculate the quality factor (QP) of the parallel resonant
band-pass filter.
QP= 6.2015
Step 26 Based on the filter quality (QP) and the center frequency (fO), calculate the expected
bandwidth (BW) of the parallel resonant band-pass filter.
BW= 162.31 Hz
Question: How did the expected bandwidth calculated from the value of QP and the center
frequency compare with the bandwidth measured on the curve plot?
The percentage difference between the two is 0.54%.
Step 27 Change the resistance of R to 5kΩ. Run the simulation again. Measure the center
frequency (fO) and the bandwidth (BW) from the curve plot and record the values.
fO=1.003 kHz
BW= 289.456 Hz
Questions: What effect did changing the resistance of R have on the center frequency of the
parallel resonant band-pass filter? What effect did changing the resistance R have on the
bandwidth of the parallel resonant band-pass filter? Explain why.
The center frequency remain constant or did not change its value while the bandwidth
changed, it increased as the resistor decrease. Therefore, the center frequency f O of a
series resonant band-pass filter is constant with change in the resistance R while the
bandwidth of the series resonant band-pass filter is inversely proportional to the
resistance R.

23. Band-Stop (Notch) Filters
Step 28 Open the circuit file Fig 2-3. Make sure that the following Bode plotter settings are
selected: Magnitude, Vertical (Log, F=0 dB, I=–20dB), Horizontal (Log, F=2 kHz,
I=500Hz)
Step 29 Run the simulation. Notice that the voltage gain in dB has been plotted between
the frequencies of 500 Hz and 2 kHz by the Bode plotter. Sketch the curve plot in
the space provided.
Question: Is the frequency response curve that of a band-stop (notch) filters? Explain why.
Yes. What was shown above is a band-stop filter because it rejects all frequencies that
are within the bandpass, and giving easy passage only to frequencies outside the
bandpass.
Step 30 Move the cursor to the center of the curve at its lowest point. Record the center
frequency (fO) on the curve plot.
fO= 1.003 kHz;
Step 31 Move the cursor to the highest point on the flat part of the curve and record the db
gain on the curve plot.
AdB= – 0.066 dB
Step 32 Move the cursor as close as possible to a point on the left side of the curve that is 3
dB down from the highest dB gain on the flat part of the curve. Record the
approximate frequency (low-cutoff frequency fC1) on the curve plot. Next, move the
cursor as close as possible to a point on the right side of the curve that is 3 dB down
from the highest dB gain on the flat part of the curve. Record the approximate
frequency (high-cutoff frequency fC1) on the curve plot.
fC1= 918.093 Hz
fC2= 1.103 kHz

24. Step 33 Based on the values of fC1 and fC2, determine the bandwidth (BW) of the series
resonant band-stop (notch) filter.
BW= 184.907 Hz
Step 34 Based on the circuit component values in Fig 2-3, calculate the expected center
frequency (fO) of the series resonant band-stop (notch) filter.
fO(COMPONENT VALUE)= 1006.58 Hz
Question: How did the calculated value of the center frequency (fO) base on circuit
component values compare with the measured value recorded on the curve plot?
The percentage difference between the calculated fO based on the circuit component
values and the measured value is only 0.36%.
Step 35 Based on the values of fC1 and fC2, calculate the center frequency (fO)
fO(fC1/fC2)= 1006.31 Hz
Question: How did the calculated value of the center frequency (fO) base on the fC1 and fC2
compare with the measured value on the curve plot?
The percentage difference between the two is 0.33%.
Step 36 Based on the circuit component values calculate the quality factor (Qs) of the series
resonant band-stop (notch) filter.
QS= 5.27
Step 37 Based on the circuit quality factor (QS) and the center frequency (fO), calculate the
expected bandwidth (BW) of the series resonant band-stop (notch) filter.
BW(EXPECTED)= 191.00 Hz
Question: How did the expected bandwidth calculated from the value of QS and the center
frequency compare with the bandwidth measured on the curve plot?
The percentage difference between the two is 3.30%.

25. Step 38 Open circuit file Fig 2-4. Make sure that the following Bode plotter settings are
selected: Magnitude, Vertical (Log, F=0 dB, I=–20dB), Horizontal (Log, F=2 kHz,
I=500Hz)
Step 39 Run the simulation. Notice that the voltage gain in dB has been plotted between the
frequencies of 500 Hz and 2 kHz by the Bode plotter. Sketch the curve plot in the
space provided.
Question: Is the frequency response curve that of a band-stop (notch) filters? Explain why.
Yes. The above curve plot is a band-stop filter because it rejects all frequencies that are
within the bandpass, and giving easy passage only to frequencies outside the bandpass.
Step 42 Move the cursor to the center of the curve at its lowest point. Record the center
frequency (fO) on the curve plot.
fO= 1.003 kHz;
Step 41 Move the cursor to the highest point on the flat part of the curve and record the dB
gain on the curve plot.
AdB= – 0.055 dB
Step 42 Move the cursor as close as possible to a point on the left side of the curve that is 3
dB down from the highest dB gain on the flat part of the curve. Record the
approximate frequency (low-cutoff frequency fC1) on the curve plot. Next, move the
cursor as close as possible to a point on the right side of the curve that is 3 dB down
from the highest dB gain on the flat part of the curve. Record the approximate
frequency (high-cutoff frequency fC1) on the curve plot.
fC1= 914.969 Hz;
fC2= 1.098 kHz

26. Step 43 Based on the values of fC1 and fC2, determine the bandwidth (BW) of the parallel
resonant band-stop (notch) filter.
BW= 183.031 Hz
Step 44 Based on the circuit component values in Fig 2-4, calculate the expected center
frequency (fO) of the parallel resonant band-stop (notch) filter.
fO(COMPONENT VALUE)= 1006.58 Hz
Question: How did the calculated values of the center frequency (fO) base on the circuit
component values compare with measured values recorded on the curve plot?
The percentage difference between the calculated fO based on the circuit component
values and the measured value is only 0.36%.
Step 45 Based on the values of fC1 and fC2, calculate the center frequency (fO).
fO(fC1/fC2)= 1002.32 Hz
Question: How did the calculated value of the center frequency (fO) base on the fC1 and fC2
compare with the measured value on the curve plot?
The percentage difference between the two is 0.07%.
Step 46 Based on the value of L and RW, calculate the quality factor (QL) of the inductor.
QL=31.62
Step 47 Based on the quality factor (QL) of the inductor, calculate the equivalent parallel
inductor resistance (REQ) across the tank circuit.
REQ= 20016.48Ω
Step 48 Based on the value of REQ and R, calculate the total parallel resistance (RP) across
the tank circuit.
RP= 3333.79Ω

27. Step 49 Based on the value of RP, calculate the quality factor (QP) of the parallel resonant
band-stop (notch) filter.
QP= 5.27
Step 50 Based on the filter quality (QP) and the center frequency (fO), calculate the expected
bandwidth (BW) of the parallel resonant band-stop (notch) filter.
BW= 191 Hz
Question: How did the expected bandwidth calculated from the value of QP and the center
frequency compare with the bandwidth measured on the curve plot?
The percentage difference between the two is 4.35%.
Step 51 Change the resistance of R to 2kΩ. Run the simulation again. Measure the center
frequency (fO) and the bandwidth (BW) from the curve plot and record the values.
fO=1.003 kHz BW= 337.136 Hz
Questions: What effect did changing the resistance of R have on the center frequency of the
parallel resonant band-stop (notch) filter? What effect did changing the resistance
R have on the bandwidth of the parallel resonant band-stop (notch) filter? Explain.
The center frequency remain constant or did not change its value while the bandwidth
changed, it increases as the resistor decreases. Therefore, the center frequency f O of a
series resonant band-pass filter is constant with the change of the value of the
resistance of resistor R while the bandwidth of the series resonant band-pass filter is
inversely proportional to the value of the resistance of resistor R.

28. CONCLUSIONS
Based on the output signal in the bode plotter the band-pass filter only allows frequencies
within the band and blocks all frequencies outside the band. Its counterpart is the band-
stop (notch) filter which blocks all frequencies within the band and allows all other
frequencies outside the band.
In addition to that, the voltage gain and the center frequency of the band-pass filter are at
the peak point of the curve plot. On the other hand, the voltage gain and the center
frequency of the band-stop filter are at the lowest point of the curve plot. Bandwidth can be
determine from subtracting the frequencies 3 dB down and up from dB gain measured at
center frequency fO.
Lastly, I concluded that the center frequency of the curve plot was not affected by the
resistance and is inversely proportional to the capacitance and inductance. Bandwidth is
not affected by capacitance, but inversely proportional to the inductance. The bandwidth in
L-C series resonant band-pass/stop filter is directly proportional to the resistance, while
bandwidth in L-C series resonant band-pass/stop filter is inversely proportional to the
resistance.