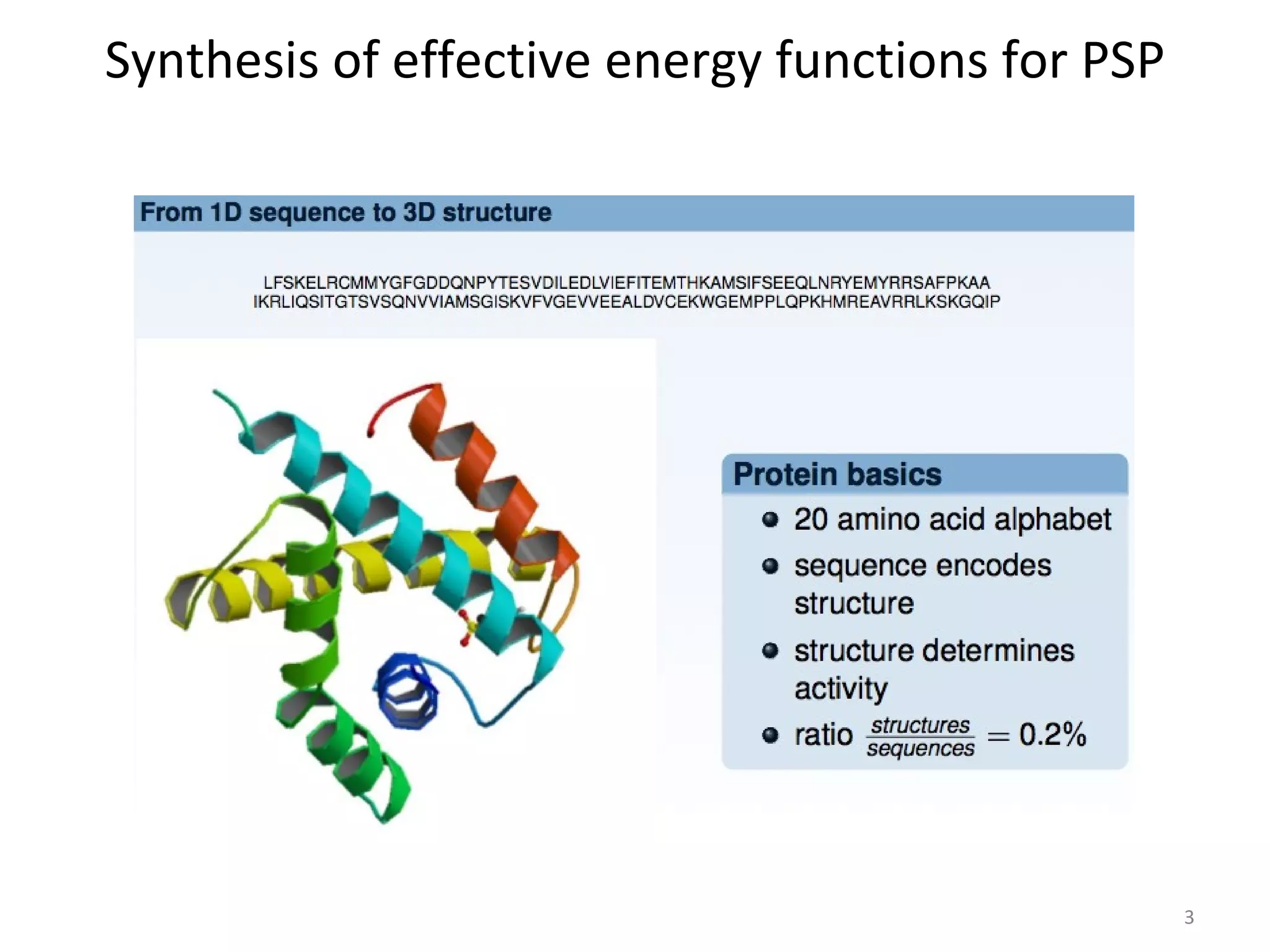
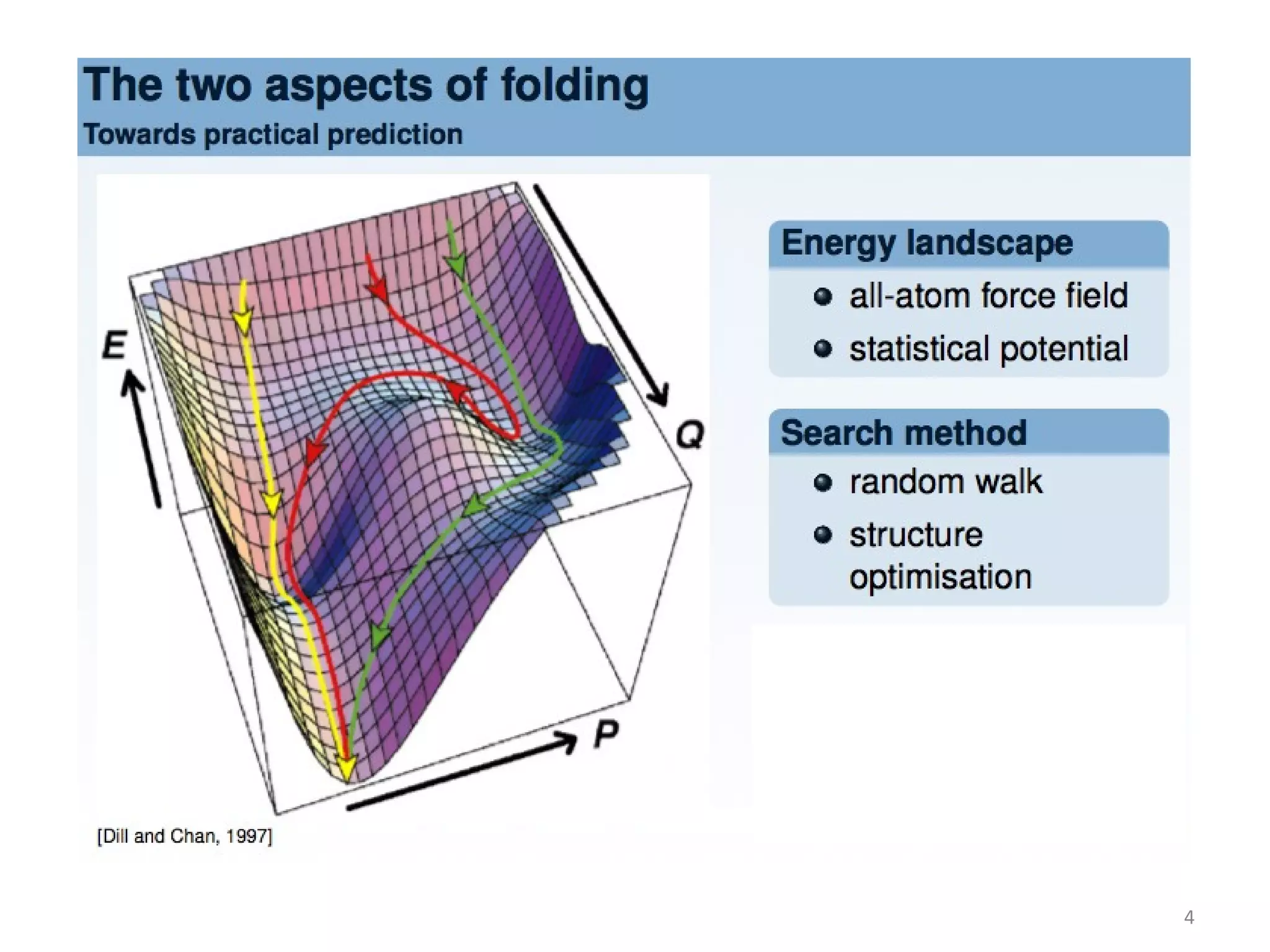
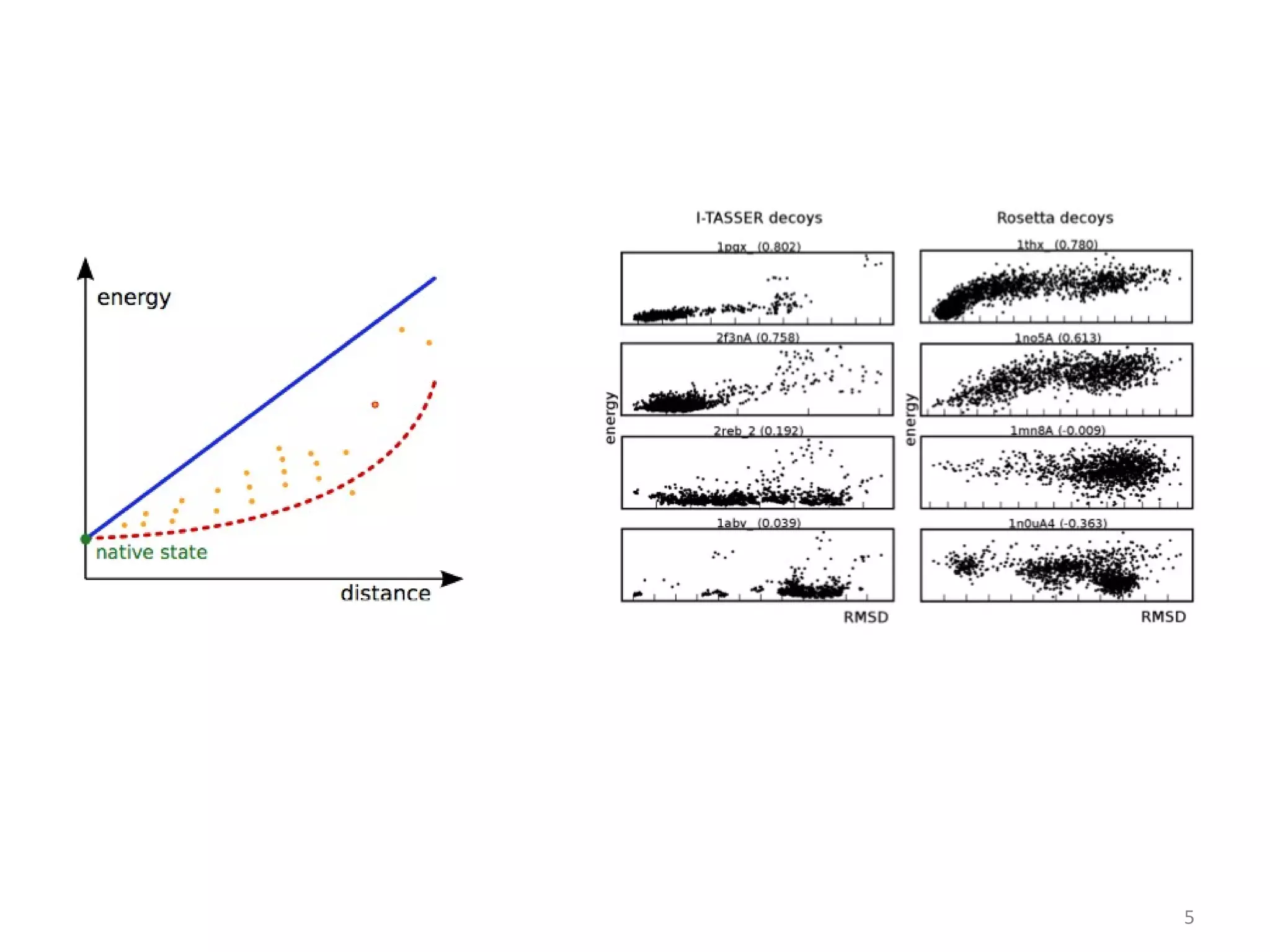
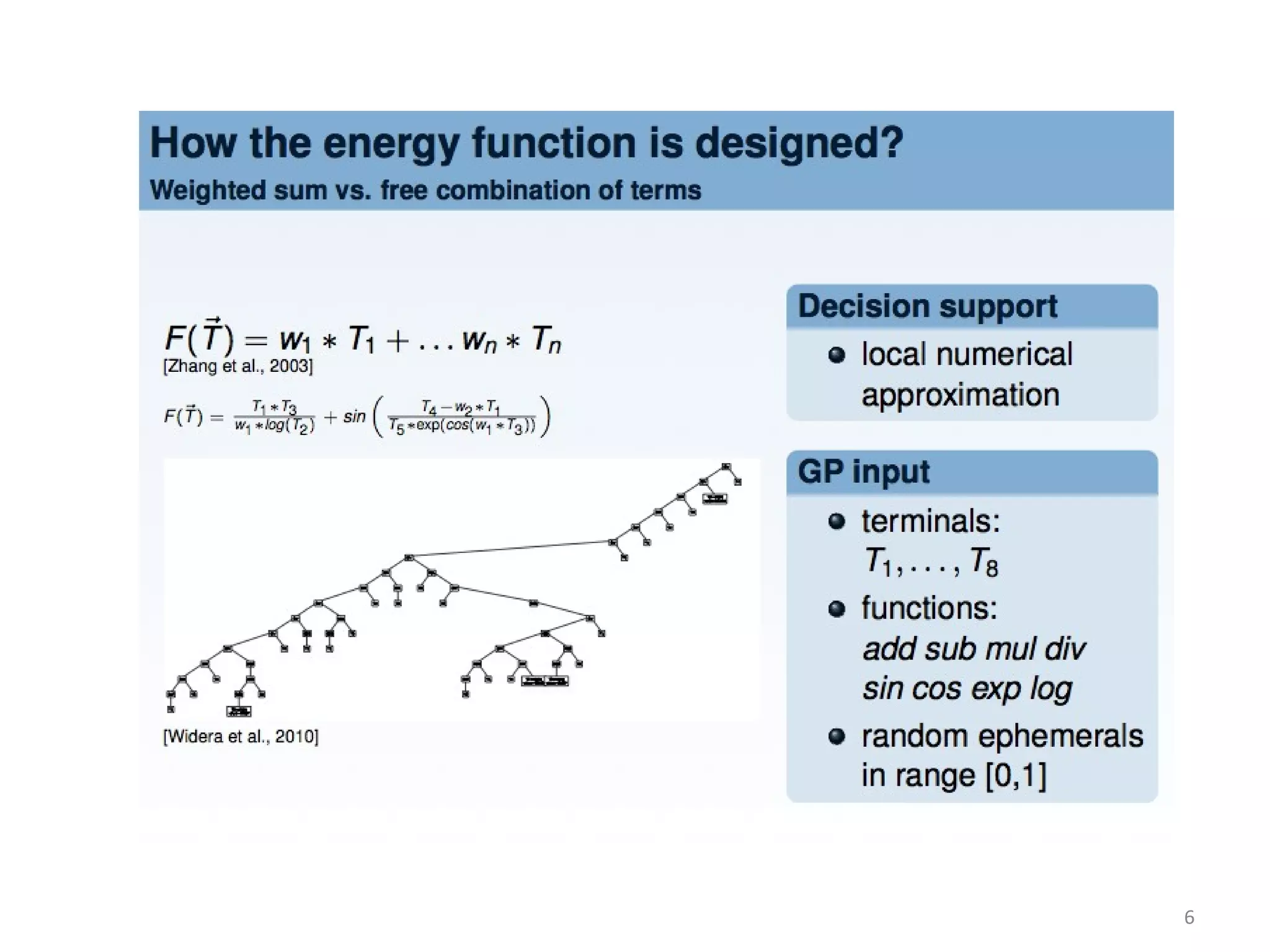
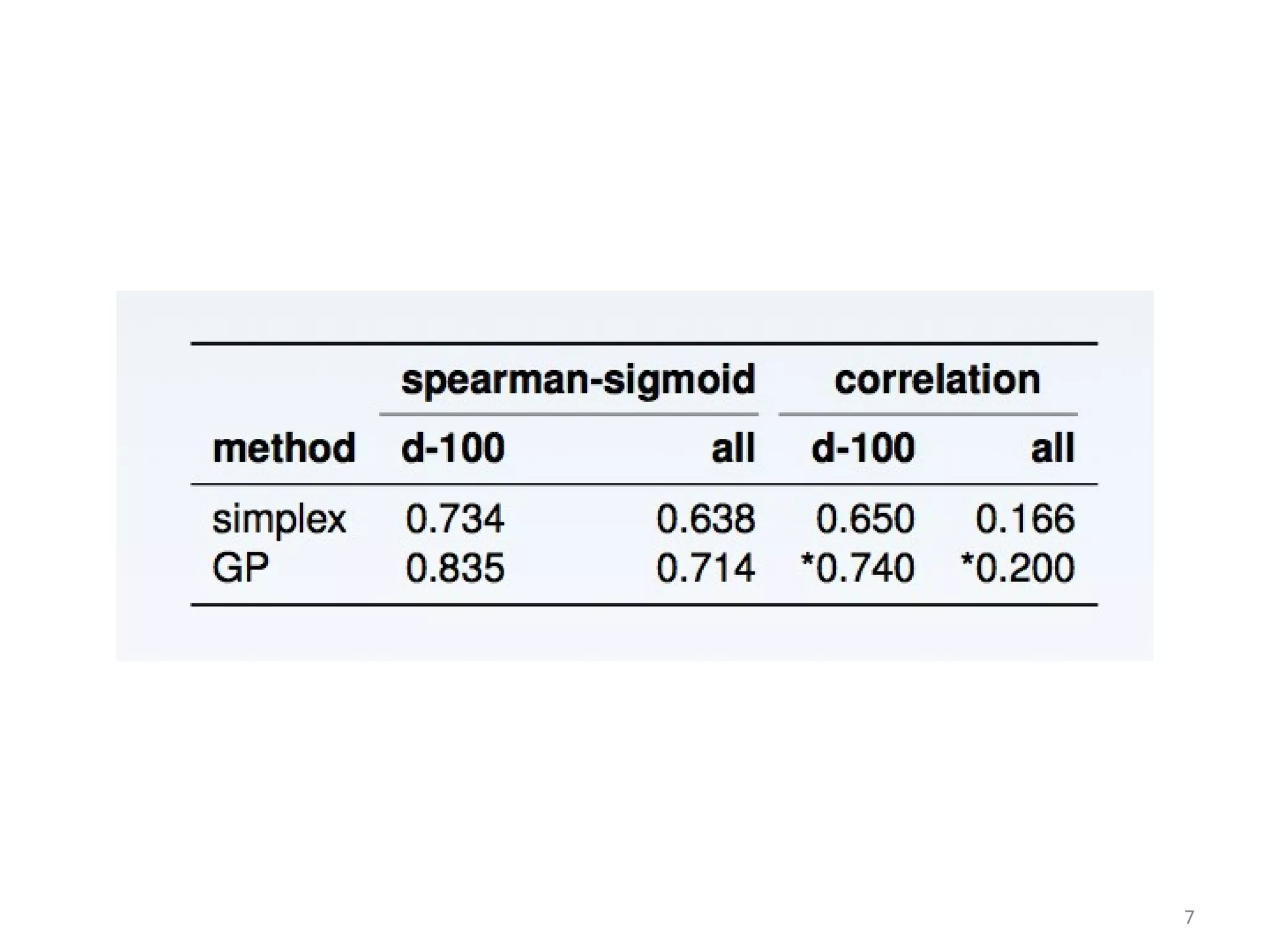
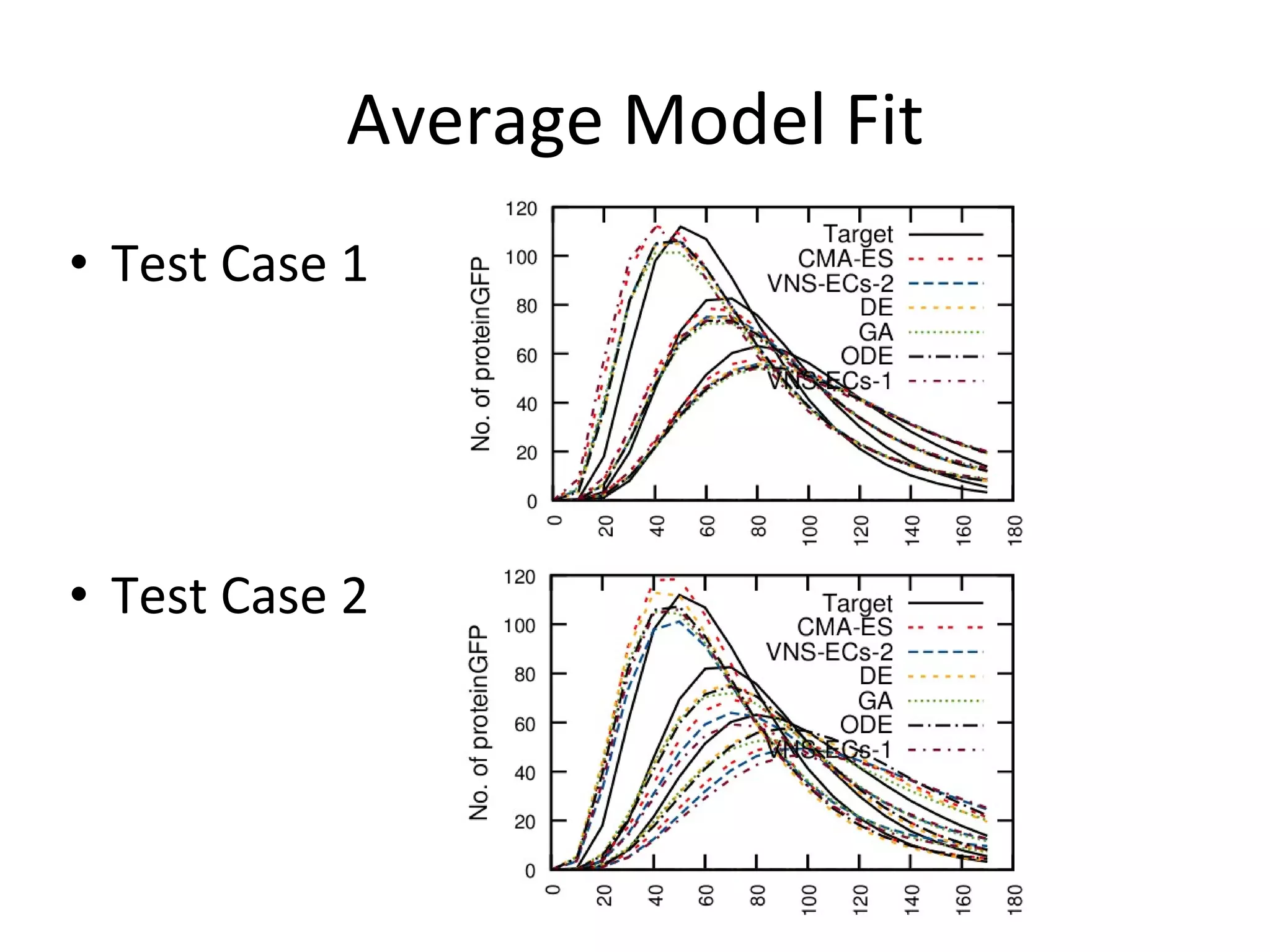
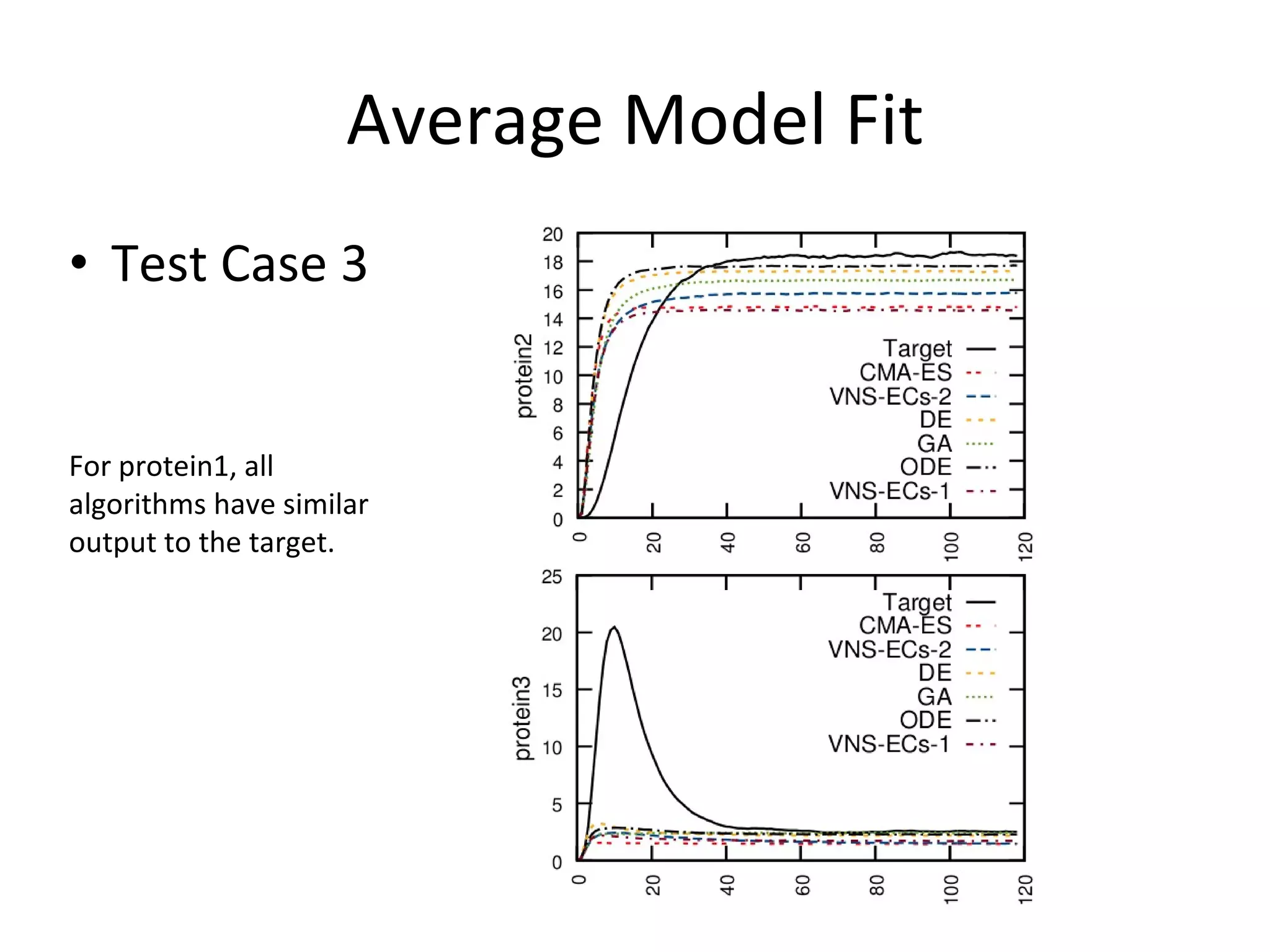
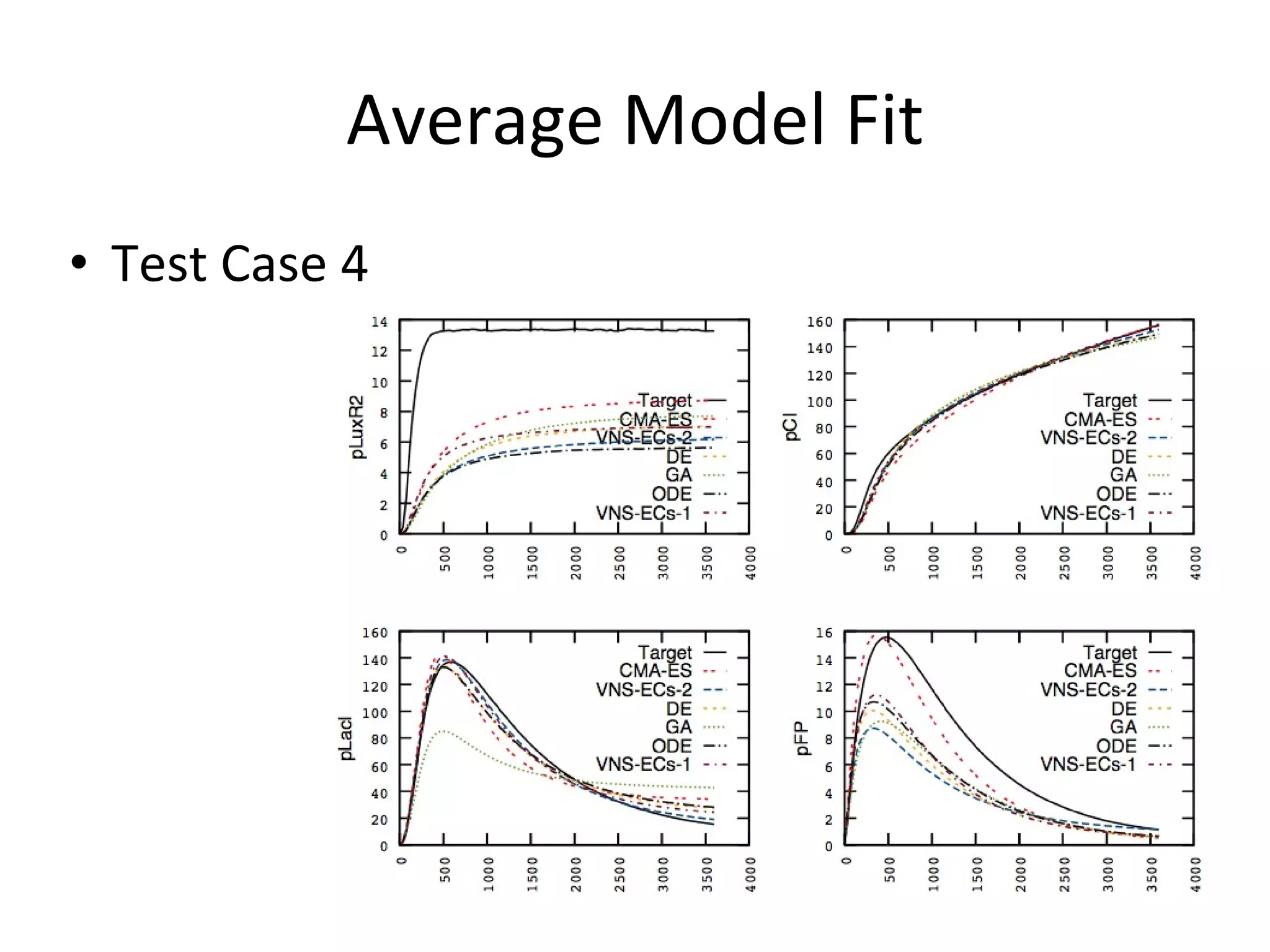
The document discusses using evolutionary symbolic discovery methods to synthesize effective energy functions for protein structure prediction and systems/synthetic biology models. It describes using genetic programming techniques to explore large combinatorial spaces of modular components and parameters to construct stochastic P systems that model cellular systems. The goal is to find structures and optimize parameters in P systems to match target models through comparing different evolutionary algorithms on test cases of increasing difficulty and dimension.

1. Evolutionary Symbolic Discovery for Bioinformatics, Systems and Synthetic Biology P. Widera, J. Bacardit, N. Krasnogor, C. Garcia-Martinez, M. Lozano

2. Symbolic Regression and Modeling are tightly linked in Bioinformatics, Systems and Synthetic Biology. We explore two problems: Synthesis of effective energy functions for PSP Synthesis of effective Systems/Synthetic Biology models Not run-of-the-mill Symbolic Regression, however: a symbolic solution is sought must fit available data must be human understandable

3. Synthesis of effective energy functions for PSP

8. Synthesis of effective Systems/Synthetic Biology models P systems are a executable modeling framework that closely mimic biological reality. Can be seen as programs that explicitly mimic the internal behavior of cell systems . Cells (and most biologists) don’t do differential calculus!

9. Motivation Learning a program with stochastic behavior vs. learning a P system. A cell is a living example of distributed computing. function f1(p1,p2,p3,p4) { if (p1<p2) and (rand<0.5) print p3 else print p4 } function f1(p1,p2,p3,p4) { if (p1<p2) RND print p3 RND else RND print p4 RND }

10. P Systems Stochastic P systems are designed for specifying and simulating cellular systems. Defined by the tuple: O is the alphabet of molecules. L={l 1 ,…,l n } is the set of labels representing different compartments. μ is the membrane structure with n≥1 membranes.

11. P Systems M l i , 1 ≤ I ≤ n , is the initial configuration of membrane i , i.e., multiset of objects over O placed inside the compartment of membrane l i . is a finite set of rules associated with compartment l i . These rules are expressed as: where o 1 , o 2 , o’ 1 , o’ 2 are multisets of objects over O and l ε L is a compartment label.

12. Modular Assembly of P Systems Modules: set of rules representing molecular interactions that occur often. Elemental modules: Degradation, complexation, unregulated gene expression, negative gene expression, etc. Combination of basic modules (building-blocks) originates more complex modules, allowing modular and hierarchical modeling with P systems. Challenge: Explore the large combinatorial space of modules and corresponding parameters.

13. Experimental Setup Compare different evolutionary algorithms to find structure & optimise parameters (kinetic constants) in P systems. Four test cases of increasing difficulty and dimension: TC1: Pulse generator for different initial conditions (13 parameters). TC2: Same problem as TC1 but with larger parameter ranges. TC3: More general pulse generator: feed-forward loop motif (18 parameters). TC4: Bandwidth detector (34 parameters). Unclear which fitness function to use

14. Target Models

15. Average Model Fit Test Case 1 Test Case 2

16. Average Model Fit Test Case 3 For protein1, all algorithms have similar output to the target.

17. Average Model Fit Test Case 4

18. Discussions & Conclusions Design of effective fitness functions: in both problems there is a lack of “silver bullet” fitness function. What to do? Besides the obviouts “fit”, include, robustness, sensitivity, parsimony and “semantic fit” terms What space is being searched? CPU hungry problems: partial evaluations? lazy evaluation? Grid/Cloud/GPGPU Human Understandability & Plausibility

19. Acknowledgements Jonathan Blake Claudio Lima Francisco Romero-Campero Karima Righetti Jamie Twycross /136 Integrated Environment Machine Learning & Optimisation Modeling & Model Checking Molecular Micro-Biology Stochastic Simulations Members of my team working on SB 2 EP/E017215/1 EP/H024905/1 BB/F01855X/1 BB/D019613/1 University of Nottingham Prof. M. Camara, Dr. S. Heeb, Dr. G. Rampioni, Prof. P. Williams Weizmann Institute of Science Prof. D. Lancet, Prof. I. Pilpel This Workshop Organisers You for listening!

20. Any Questions? www.synbiont.org /136 Become a member and have access to a large international community of Synthetic Biologists