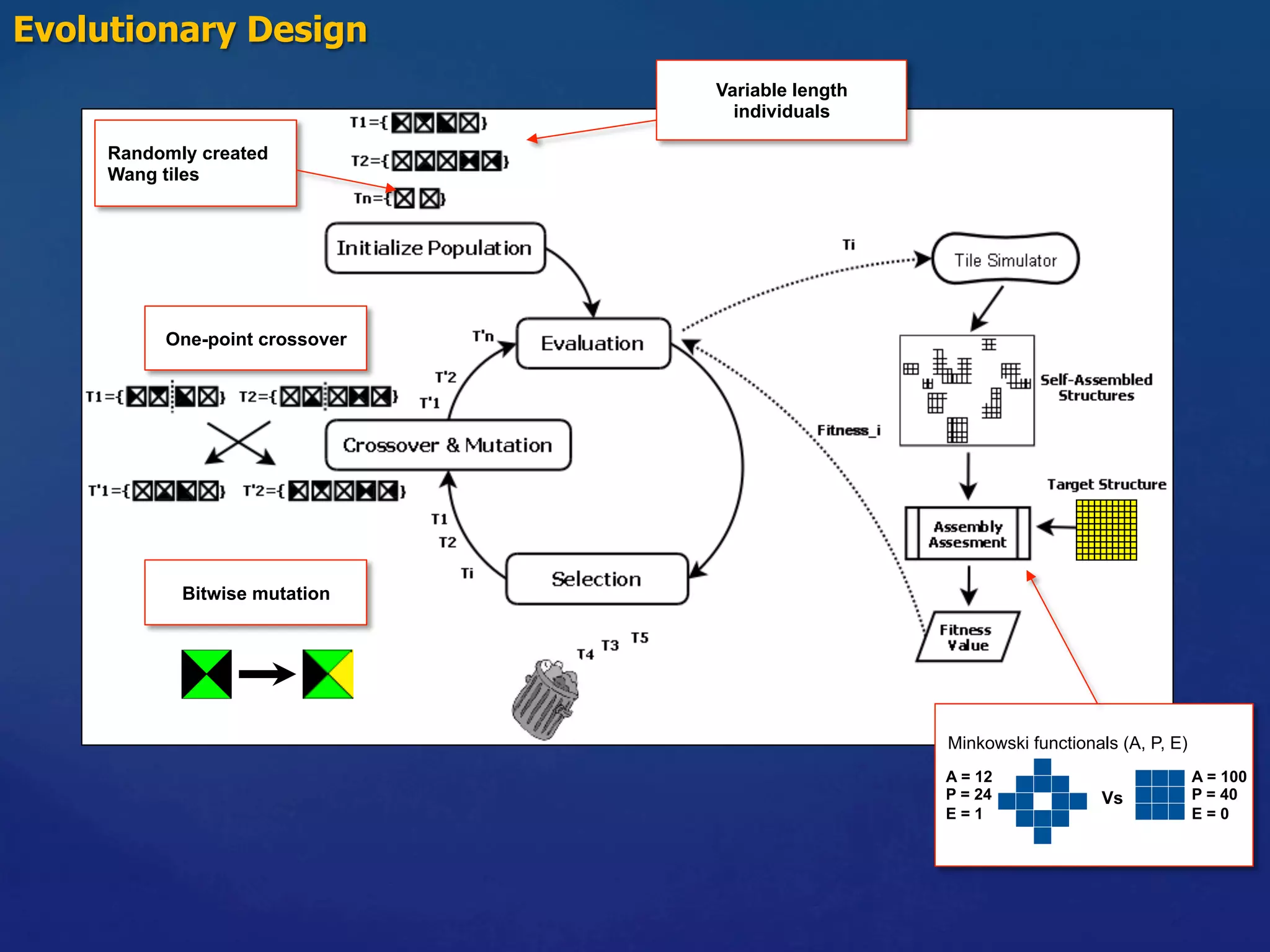
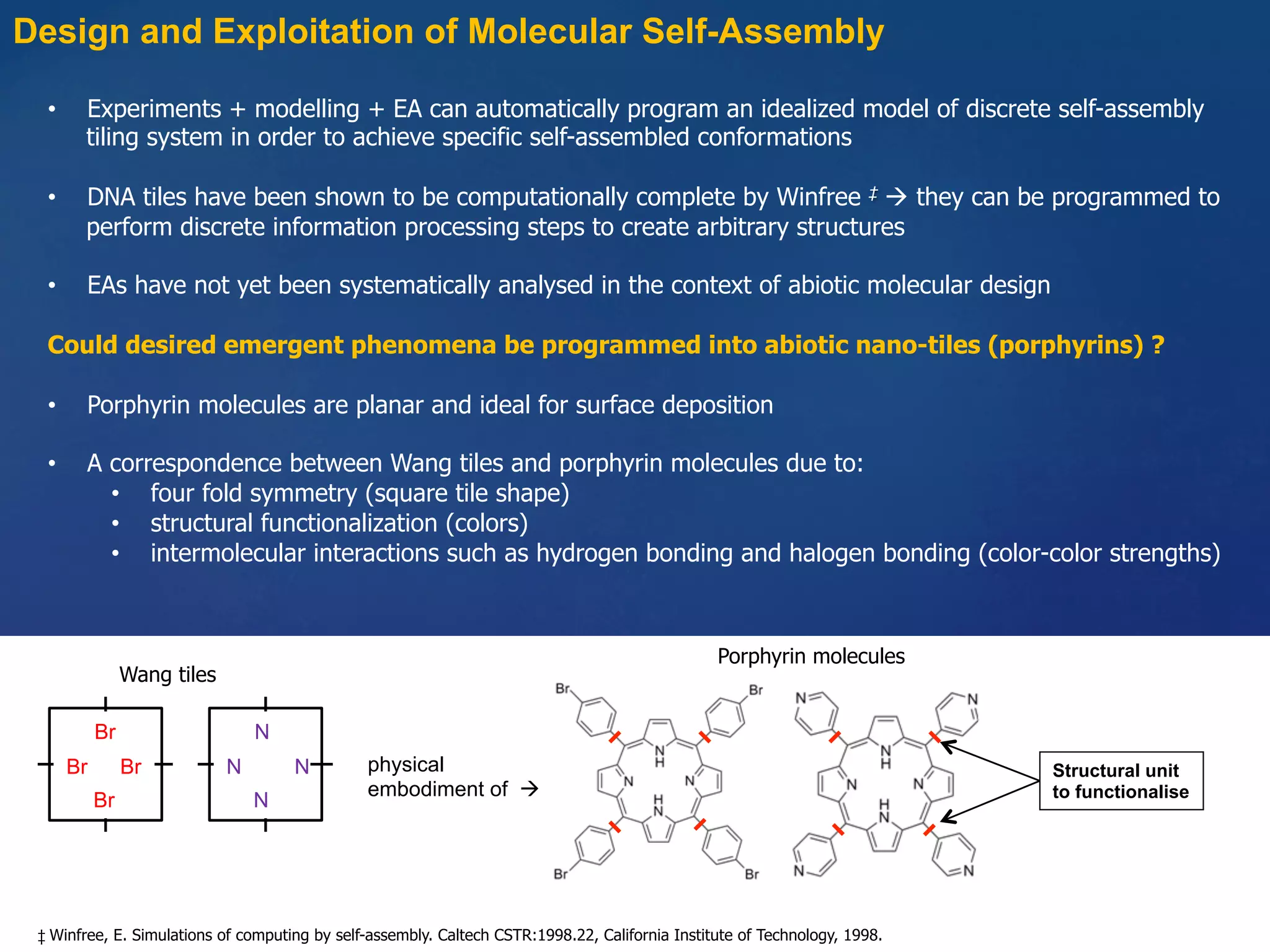
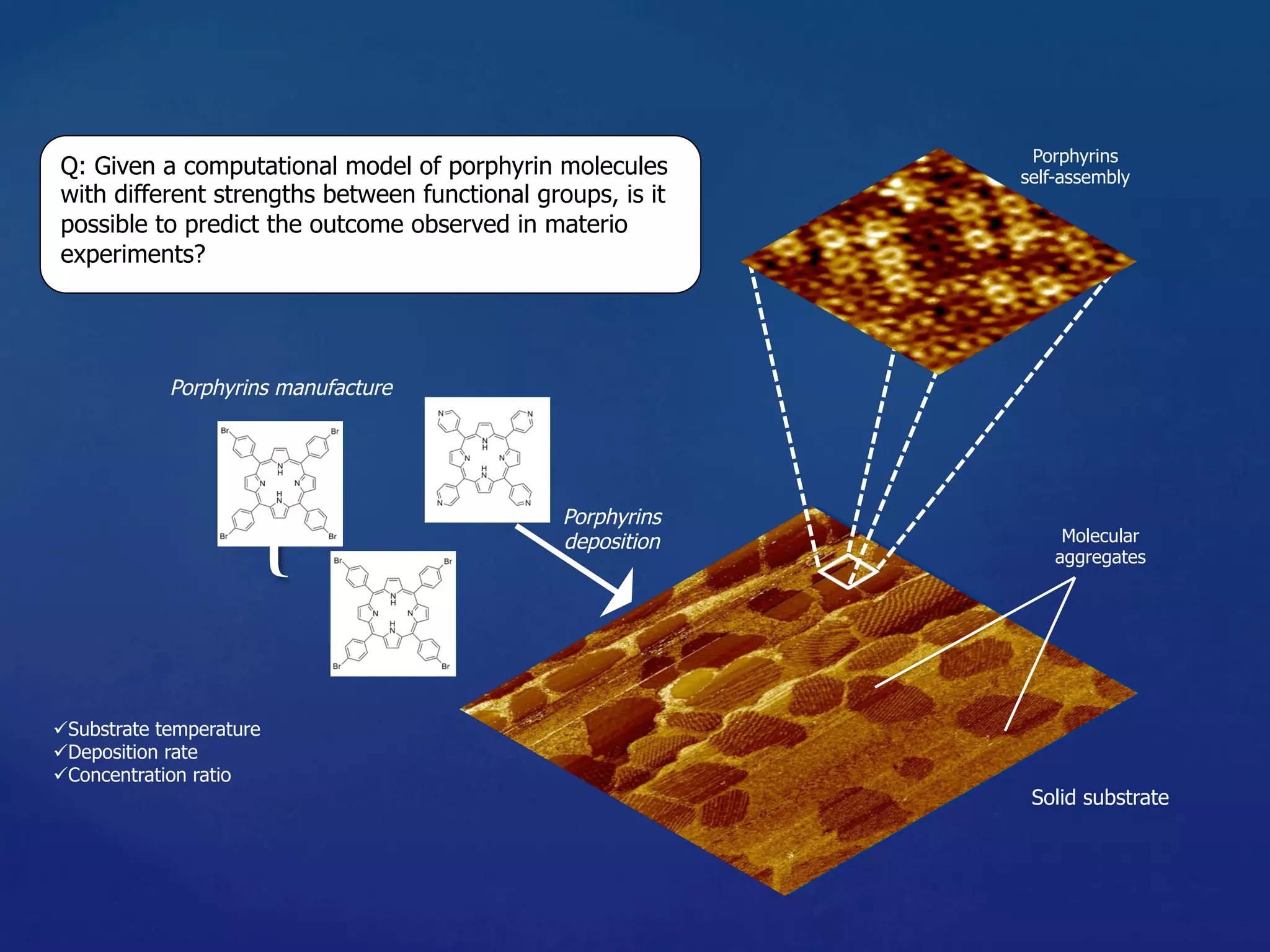
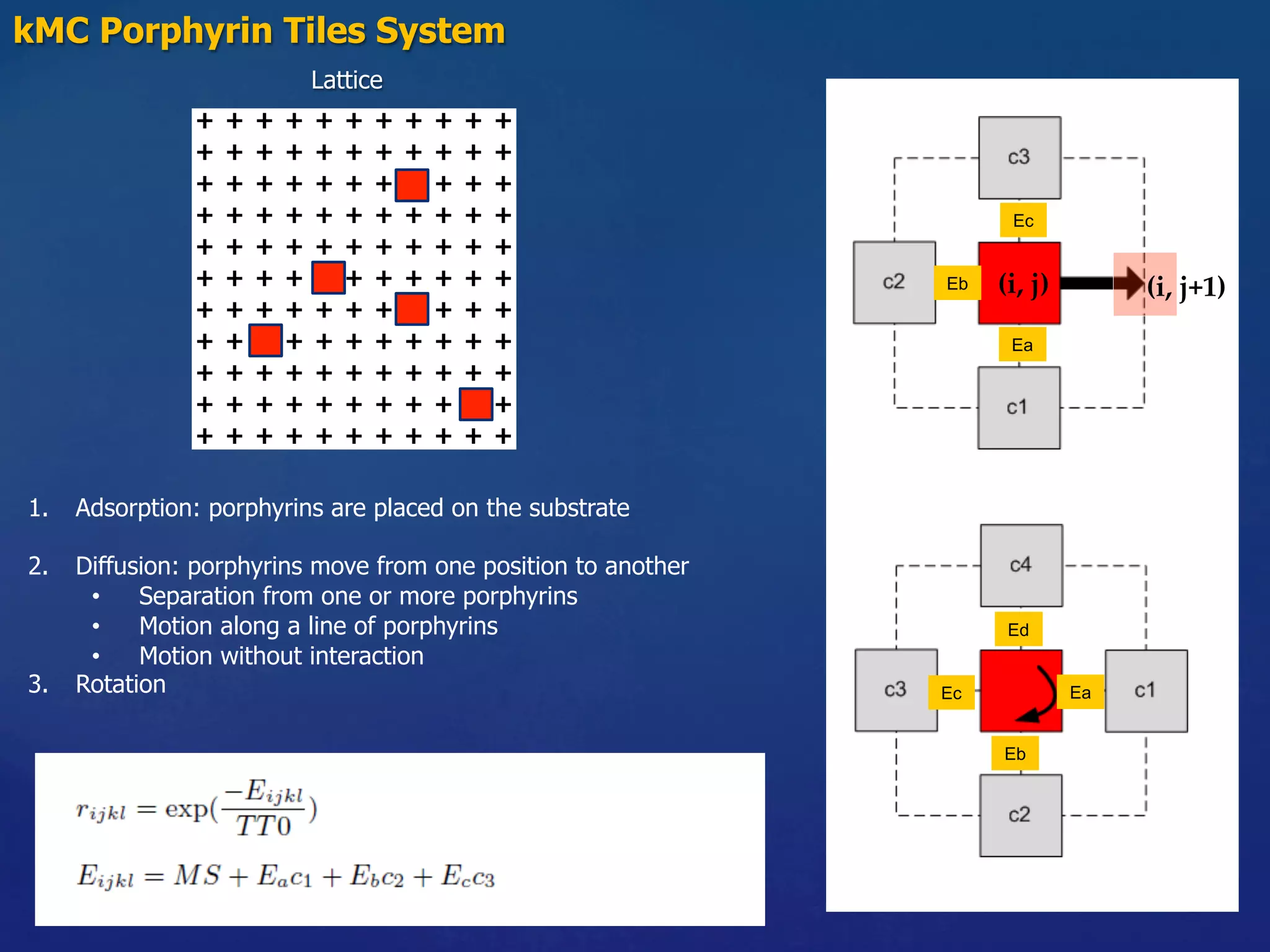
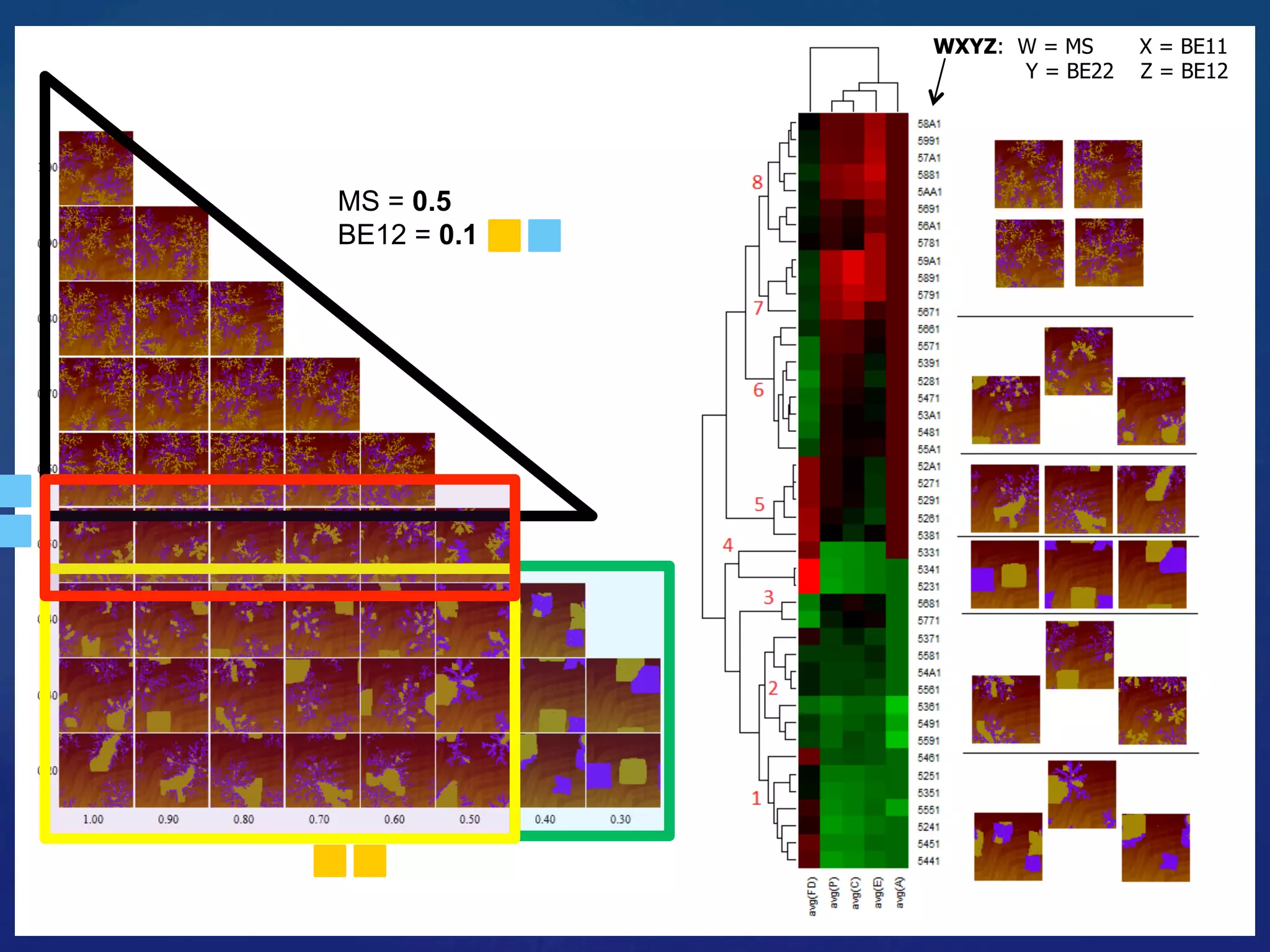
This document discusses using porphyrin-based nano-tiles for evolvable designs and computation through self-assembly. It outlines research on: 1) Using evolutionary algorithms to program self-assembly of Wang tiles to achieve target structures and applying this approach to programmable self-assembly of porphyrin molecules. 2) Modeling self-assembly of porphyrin molecules with different binding strengths using kinetic Monte Carlo simulations to predict experimental outcomes. 3) Analyzing self-assembled structures from the simulations using metrics like Minkowski functionals and Kolmogorov complexity to characterize computation and information processing during self-assembly.

1. {
Evolvability of Designs and Computation
with Porphyrins-based Nano-tiles
N. Krasnogor
ICOS Research Group
Newcastle University
Visit to the University of Granada, Spain - 2015
Presentation in collaboration with German
Terrazas & Hector Zenil

2. Outline
• Introduction
Unconventional computing
Self-assembly
Key problems on self-assembly
• Instance of the backward problem
Self-assembly Wang tiles system
Evolutionary design optimisation
• Instance of forward problem
Tiles as model of porphyrin molecules
kMC porphyrin tiles system
Computational Analysis of Self-Assembly Structures
• Kolmogorov Complexity of & Information Processing
during self-assembly

3. Unconventional Computing
• A Research Vision
Programmable algorithmic entry to the vast world of
nanoscale physical, chemical & biological systems and
processes
Algorithmic and Artificial Living Matter (ALMA)
ComputerScience
Embedded behavior
Information & Algorithms
Complexity
Robustness
Tradeoffs
How does “The Logistics of Small Things” look like?
How (?) do you gain algorithmic entry into

4. The Spatial Scales Involved

5. • Forward problem (prediction): given a set of self-assembling entities + environmental
conditions , how the final aggregates looks like?
• Backward problem (programmability): given a final desired outcome of a self-assembly
process, how the self-assembly entities + environmental conditions should be
programmed?
• Yield problem (production/control): given a self-assembling system, how many of the
desired aggregates one can expect and how to maximise it ?
Self-assembly: A phenomenon in which complex structures are formed from many
autonomous components with no master plan or external influences. Unlike self-
organisation, structures are formed close to equilibrium, i.e. there is no flow of matter or
energy in the system.

6. Backward Problem Instance

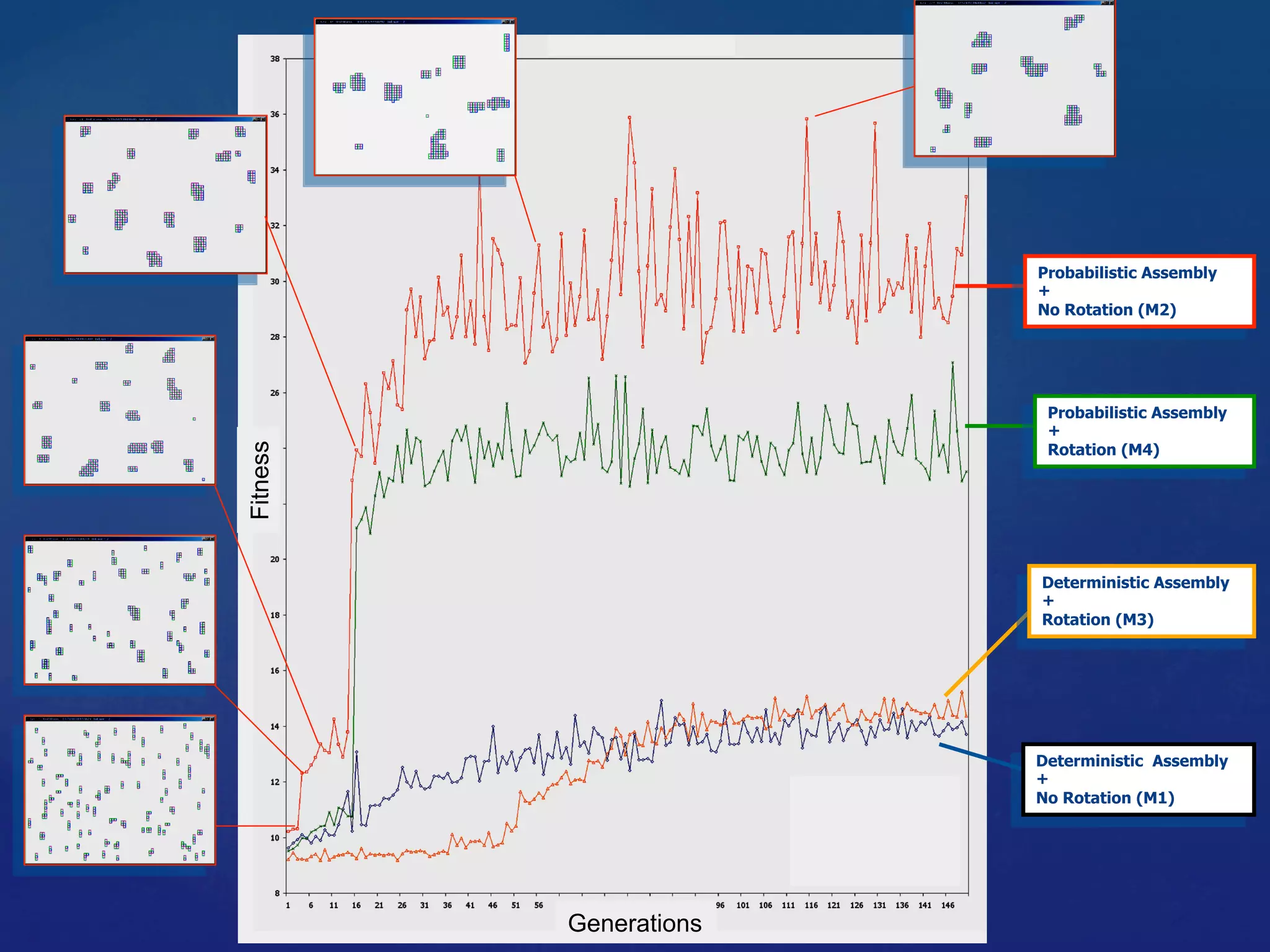
7. Self-assembly Wang Tiles Programmability Self-Assembly Wang Tiles
Target structures: square-like shapes
N tiles
Ntiles
Tiles System
• Finite size
square-site lattice
(300x300)
• Fixed T = 4
• Fixed M
Q: Is it possible to program
the family tiles needed to
obtain arbitrary structures by
means of SA ?
M [color, color] : strength
1 3 7 5 2
3 5 4 7 1
7 4 8 2 9
5 7 2 3 8
2 1 9 8 2

8. Minkowski functionals (A, P, E)
A = 12
P = 24
E = 1
A = 100
P = 40
E = 0
Evolutionary Design
Variable length
individuals
Randomly created
Wang tiles
Bitwise mutation
Vs
One-point crossover

9. Probabilistic Assembly
+
No Rotation (M2)
Probabilistic Assembly
+
Rotation (M4)
Deterministic Assembly
+
Rotation (M3)
Deterministic Assembly
+
No Rotation (M1)
Generations
Fitness

10. Design and Exploitation of Molecular Self-Assembly
• Experiments + modelling + EA can automatically program an idealized model of discrete self-assembly
tiling system in order to achieve specific self-assembled conformations
• DNA tiles have been shown to be computationally complete by Winfree ‡ à they can be programmed to
perform discrete information processing steps to create arbitrary structures
• EAs have not yet been systematically analysed in the context of abiotic molecular design
Could desired emergent phenomena be programmed into abiotic nano-tiles (porphyrins) ?
• Porphyrin molecules are planar and ideal for surface deposition
• A correspondence between Wang tiles and porphyrin molecules due to:
• four fold symmetry (square tile shape)
• structural functionalization (colors)
• intermolecular interactions such as hydrogen bonding and halogen bonding (color-color strengths)
‡ Winfree, E. Simulations of computing by self-assembly. Caltech CSTR:1998.22, California Institute of Technology, 1998.
R3
R2R4
R1Br
Br
Br Br
R3
R2R4
R1N
N
N N physical
embodiment of à
Structural unit
to functionalise
Wang tiles
Porphyrin molecules

11. Forward Problem Instance

12. { Porphyrins
deposition
Porphyrins
self-assembly
Solid substrate
Porphyrins manufacture
Molecular
aggregates
ü Substrate temperature
ü Deposition rate
ü Concentration ratio
Q: Given a computational model of porphyrin molecules
with different strengths between functional groups, is it
possible to predict the outcome observed in materio
experiments?

13. Lattice
1. Adsorption: porphyrins are placed on the substrate
2. Diffusion: porphyrins move from one position to another
• Separation from one or more porphyrins
• Motion along a line of porphyrins
• Motion without interaction
3. Rotation
Ea
Eb
Ec
Eb
EaEc
Ed
kMC Porphyrin Tiles System
(i, j) (i, j+1)

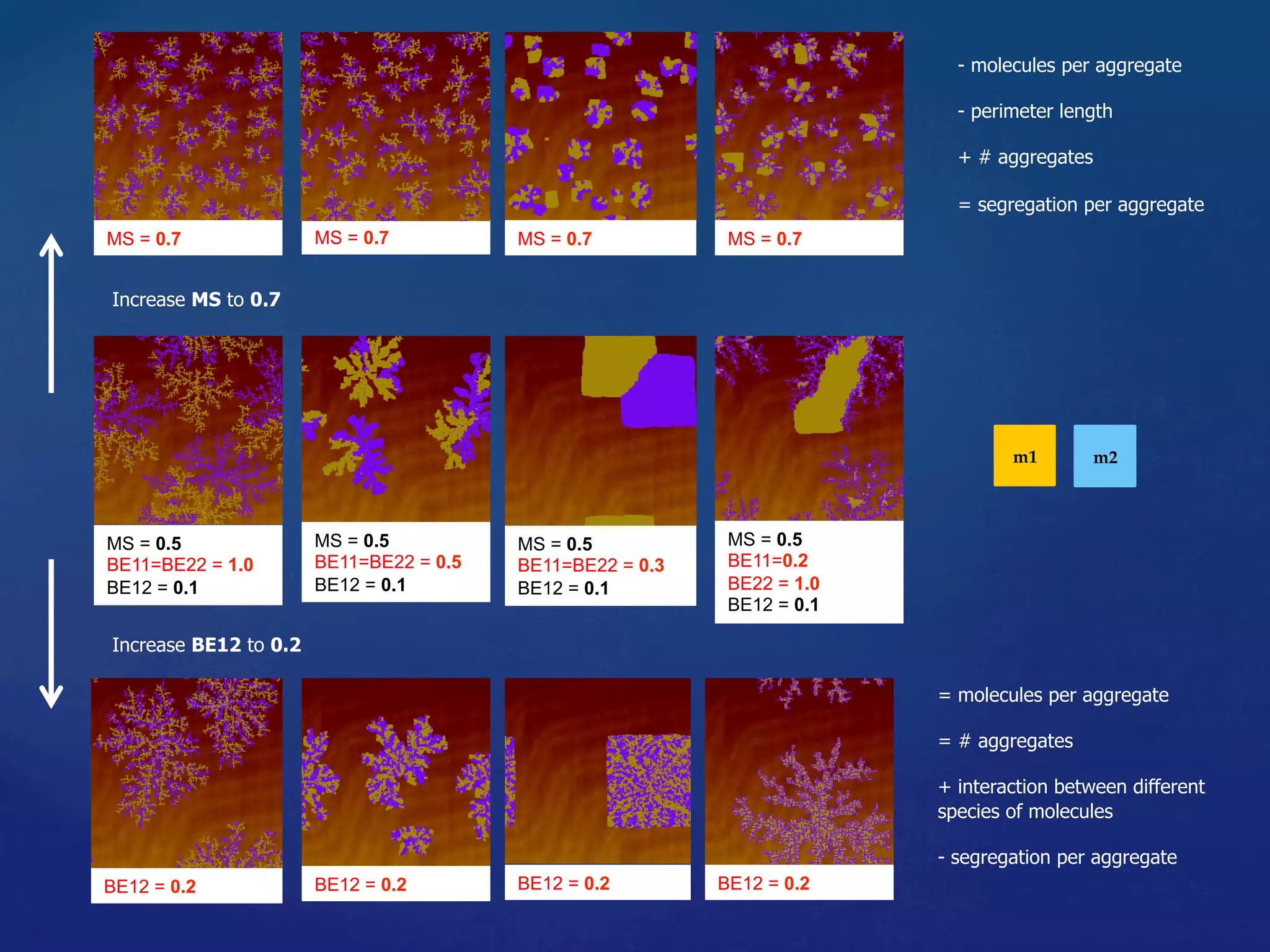
14. Molecule types: m1, m2
Fixed Parameters
Substrate: 256 x 256
Coverage: 25%
Variable Parameters
Molecule-Substrate (MS) = [0.5, 1.0] res. 0.1 eV
Binding strength (BE11) = [0.1, 1.0] res. 0.1 eV
Binding strength (BE22) = [0.1, 1.0] res. 0.1 eV
Binding strength (BE12) = [0.1, 1.0] res. 0.1 eV
m1
1
1
1
1
2
m2 2
2
2
Experiments
m1 m1
m2 m2
m1 m2

15. MS = 0.5
BE11=BE22 = 1.0
BE12 = 0.1
MS = 0.5
BE11=BE22 = 0.5
BE12 = 0.1
MS = 0.5
BE11=0.2
BE22 = 1.0
BE12 = 0.1
MS = 0.5
BE11=BE22 = 0.3
BE12 = 0.1
BE12 = 0.2 BE12 = 0.2 BE12 = 0.2BE12 = 0.2
= molecules per aggregate
= # aggregates
+ interaction between different
species of molecules
- segregation per aggregate
Increase BE12 to 0.2
MS = 0.7 MS = 0.7MS = 0.7
- molecules per aggregate
- perimeter length
+ # aggregates
= segregation per aggregate
Increase MS to 0.7
MS = 0.7
m1 m2

16. WXYZ: W = MS X = BE11
Y = BE22 Z = BE12
MS = 0.5
BE12 = 0.1

17. A = 1370
P = 192
A = 1687
P = 259
A = 304
P = 101
A = 1017
P = 150
A = 720
P = 139
A = 675
P = 144
A = 1453
P = 240
A = 934
P = 176
A = 1446
P = 235
avg(A) = 1067.33
avg(P) = 181.77
Mol-sub = 0.8
BE12=BE11=BE22 = 0.1
avg(A) = 1257.76
avg(P) = 122.30
mol-sub = 0.7
BE11=BE22=BE12 = 0.3
avg(A) = 819.2
avg(P) = 108.6

18. Iso-functionalised porphyrins
Hetero-functionalised porphyrins
We can define families:
Homogeneous iso-functionalised porphyrins
Homogeneous hetero-functionalised porphyrins
Heterogeneous iso-functionalised porphyrins
Heterogeneous hetero-functionalised porphyrins
Towards Programmable Porphyrin nano-tiles
A porphyrin
molecule
Tetra-Iodo-Phenyl
porphyrin
Tetra-Bromo-Phenyl
porphyrin
Tetra-Carboxy-Phenyl
porphyrin
Tri-carboxylic-monopyridyl
porphyrin
Dinitro-diiodo
porphyrin
Structural unit
to functionalise
Binding energy
values from
phys/chem

19. Tetra-Pyridyl Porphyrin (TPyP) on Au(111) Tetra-Nitro-Phenyl Porphyrin (TNPP) on Au(111)
Tetra-Nitro-Phenyl
Porphyrin (TNPP) on
Au(110)
Tetra-Bromo-Phenyl Porphyrin (TBrPP) on Au(111)

20. Ques%on : Is it possible to program discrete computa/onal
processes that generate specific spa/al self-assembled
pa6erns ?
20

21. Backbone
Self-assembly coun6ng
process
• Blue porphyrin-6les act as counters1,2 “seeded” via
red porphyrin-6les
• Backbones are spa6al limits controlling blue-
porphyrin-6les assembly
1 Q. Cheng et al. Op6mal self-assembly of counters at temperature two. In Founda&ons of Nanosciense, 2004.
2 P. Moisset. Computer aided search for op6mal self-assembly systems. In N. Krasnogor et al. (Eds.), Systems Self-Assembly Mul&disciplinary Snapshots, 2008.
m1
m2
Embedded Discrete Process of Computa%on (I)
21
Backbone
Es = 0.50
E11 = 1.00
E22 = 0.20
E12 = 0.20
Es = 0.60
E11 = 0.40
E22 = 0.20
E12 = 0.10

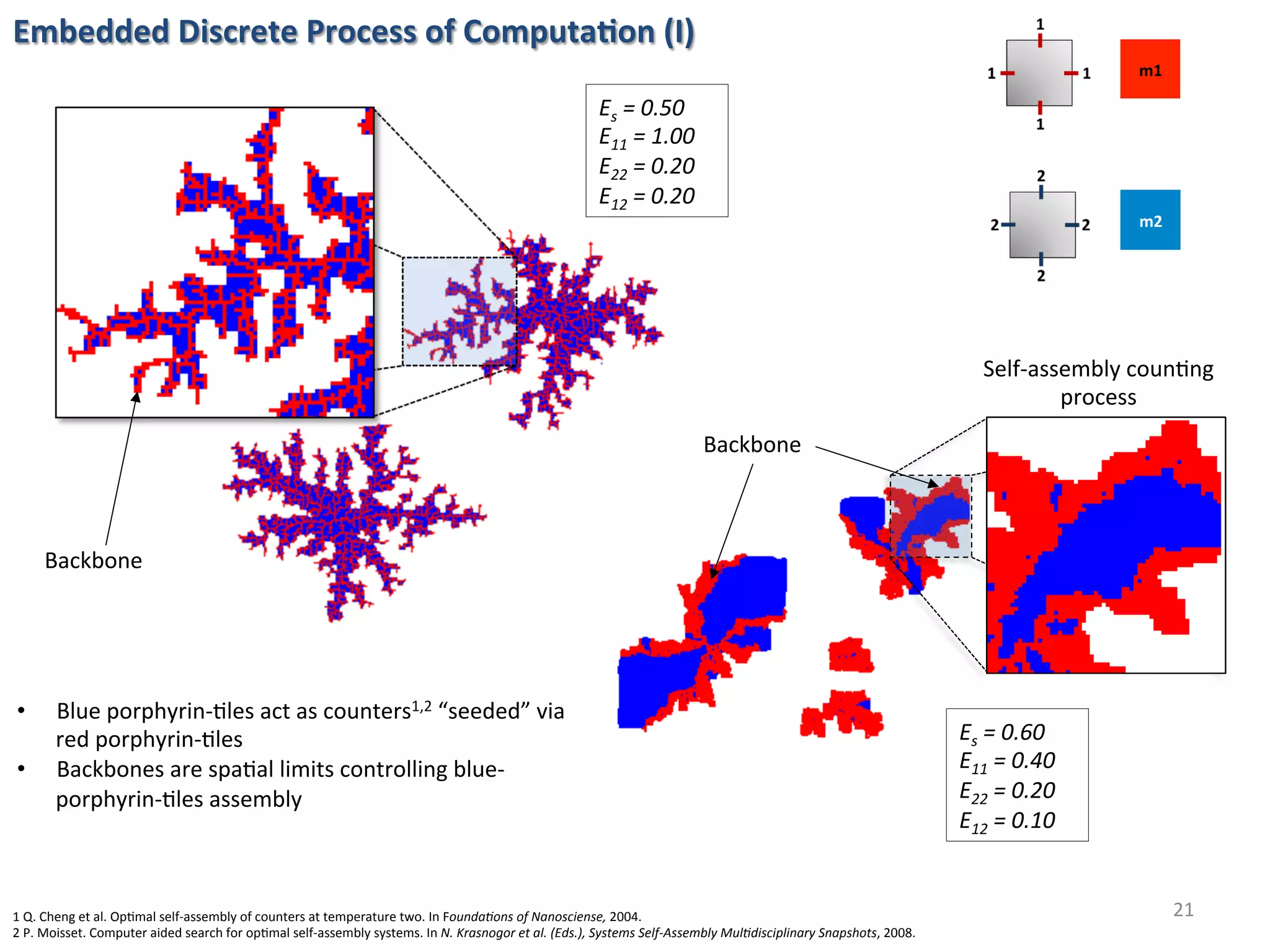
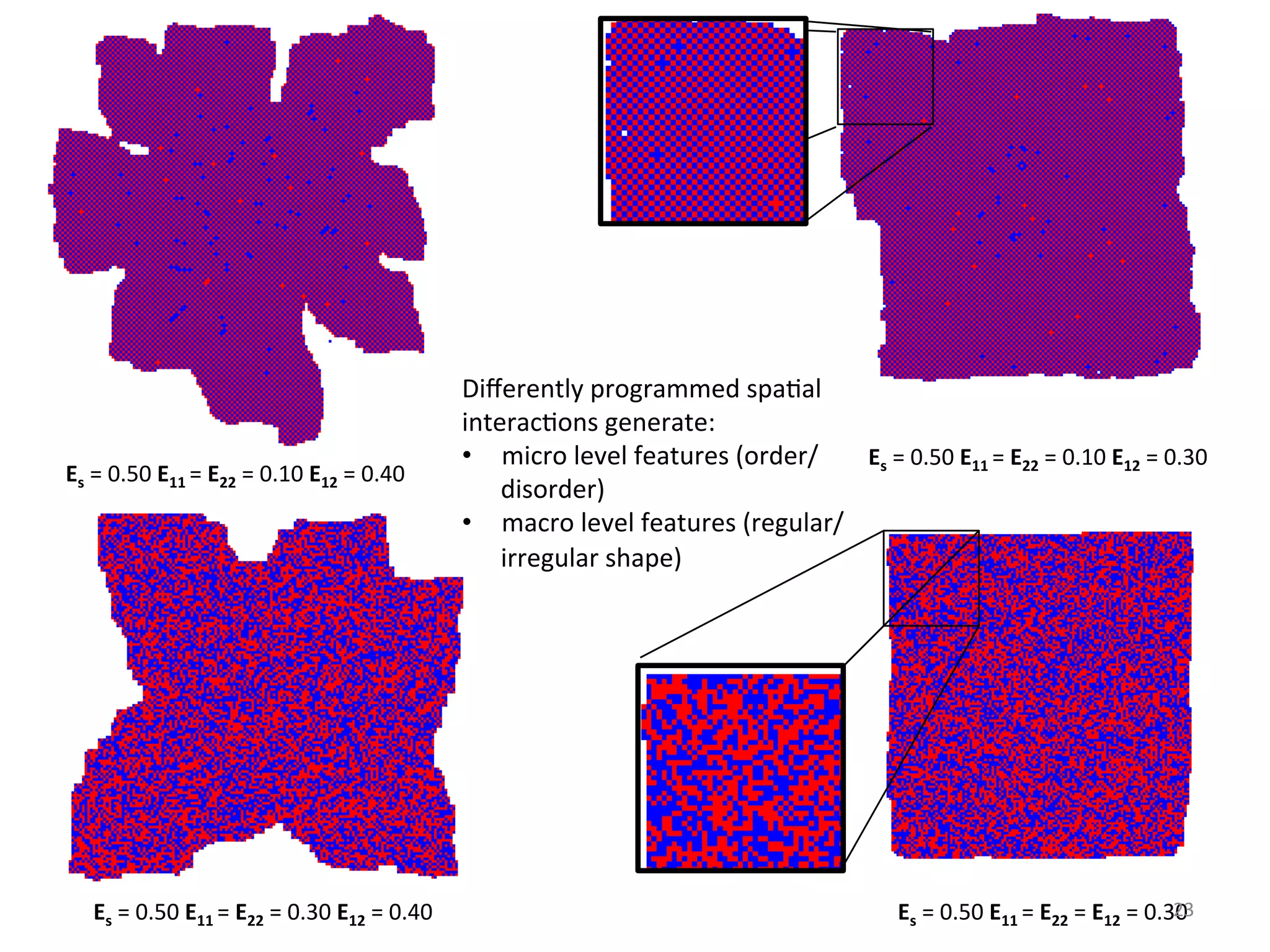
22. Embedded Discrete Process of Computa%on (II)
22
Checkers paLern
(spa6al interac6ons)
• Highly ordered self-assembled structure
• Spontaneous internal arrangements
• Globally complex shape with locally
simple organisa6on
λ (y)
λ (y)
(x)
(ε) (ε)
(x)
q1
q2
ε, x, y Є [0, 1]
ε + x + y = 1
x >> ε >> y
Computed by a finite state
machine-like process
ε: probability of mistaking symbol
λ: new diagonal begins

23. Es = 0.50 E11 = E22 = 0.10 E12 = 0.40
Es = 0.50 E11 = E22 = 0.10 E12 = 0.30
Es = 0.50 E11 = E22 = 0.30 E12 = 0.40 Es = 0.50 E11 = E22 = E12 = 0.30
Differently programmed spa6al
interac6ons generate:
• micro level features (order/
disorder)
• macro level features (regular/
irregular shape)
23

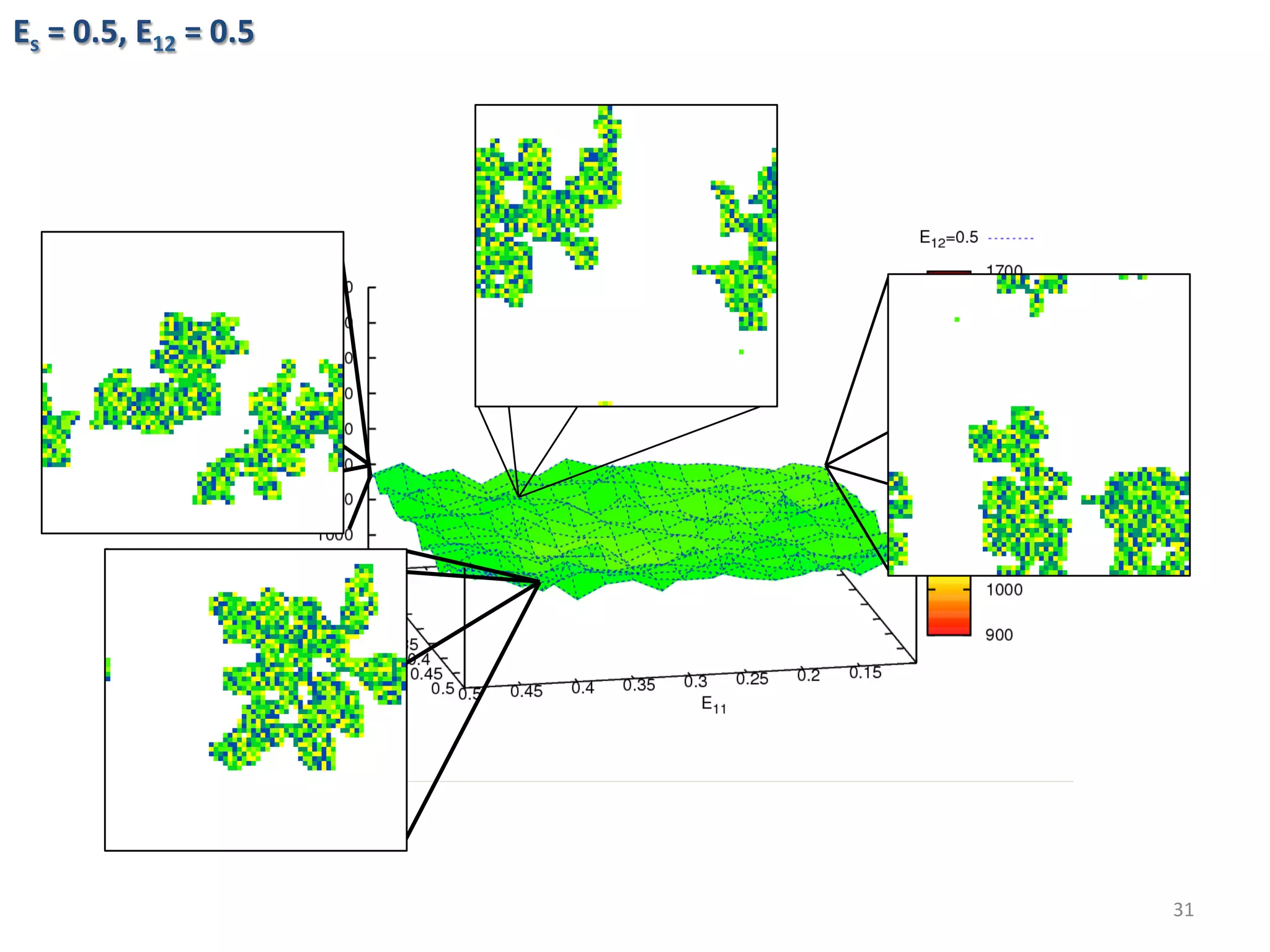
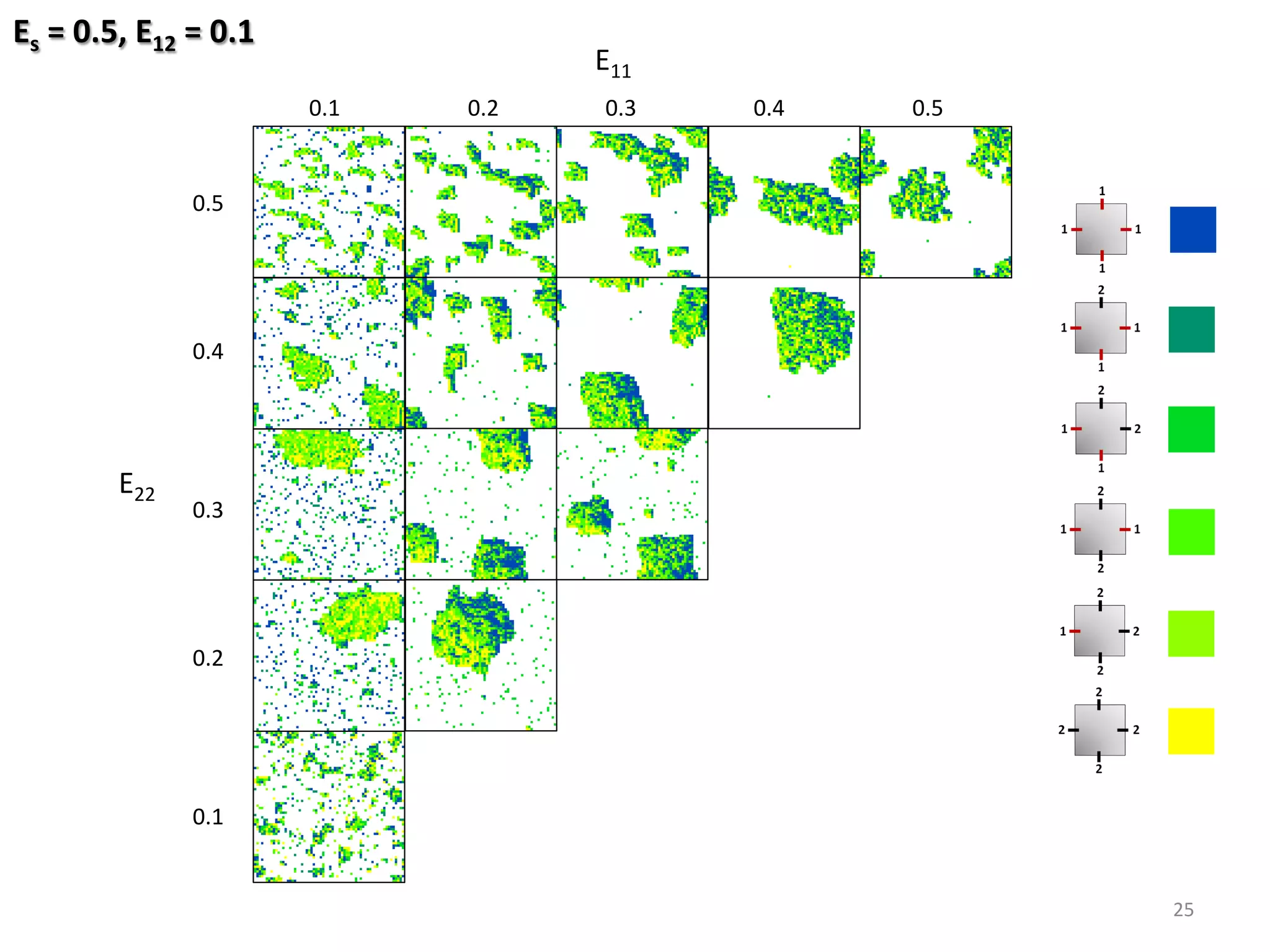
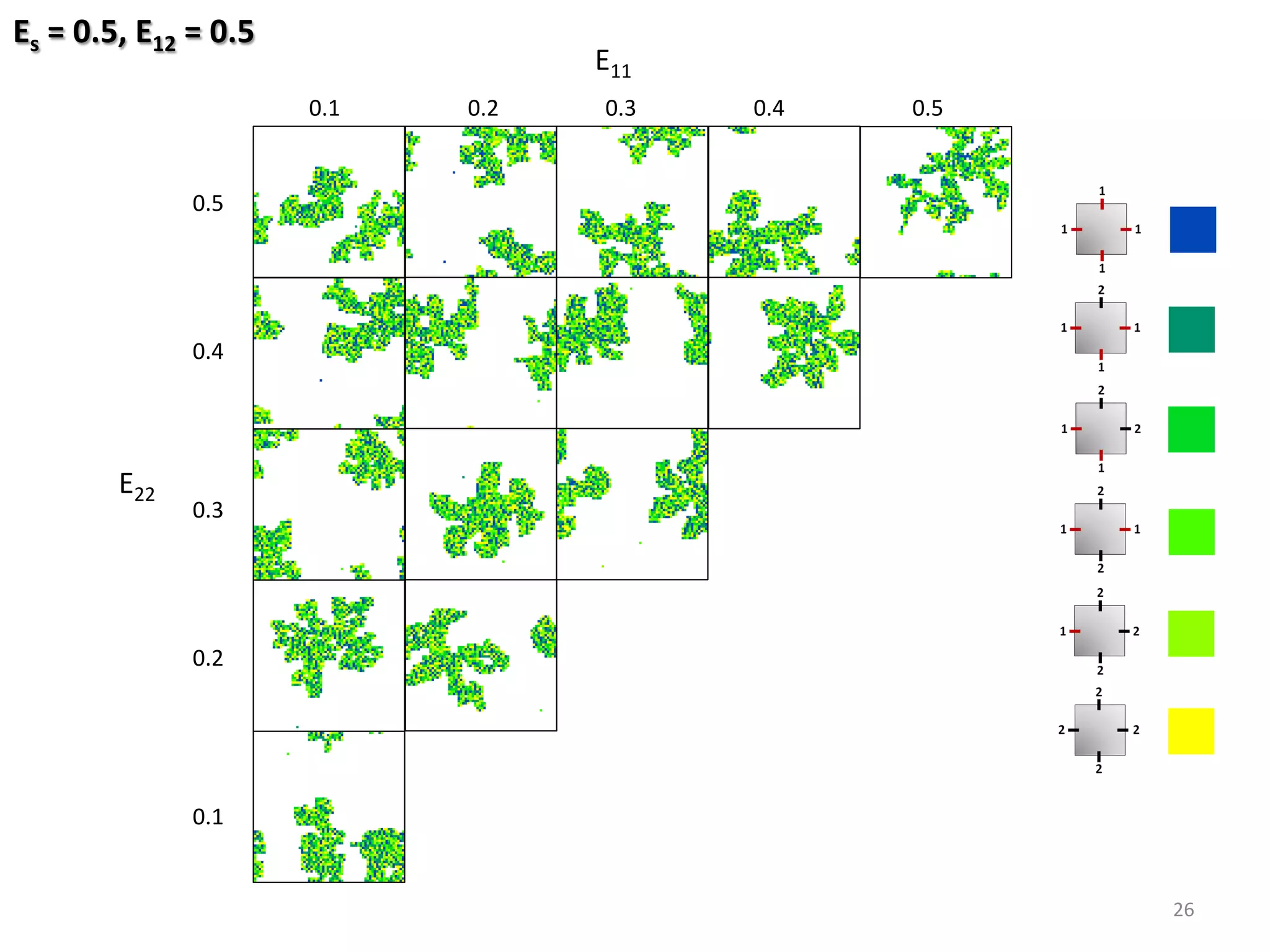
24. Fixed Parameters
Substrate: 64 x 64
Coverage: 25%
Variable Parameters
Molecule-Substrate (ES) = [0.5, …, 0.7] res. 0.1 eV
Binding strength (E11, E22) = [0.1, …, 0.5] res. 0.025 eV
Binding strength (E12) = [0.1, …, 0.5] res. 0.1 eV
24
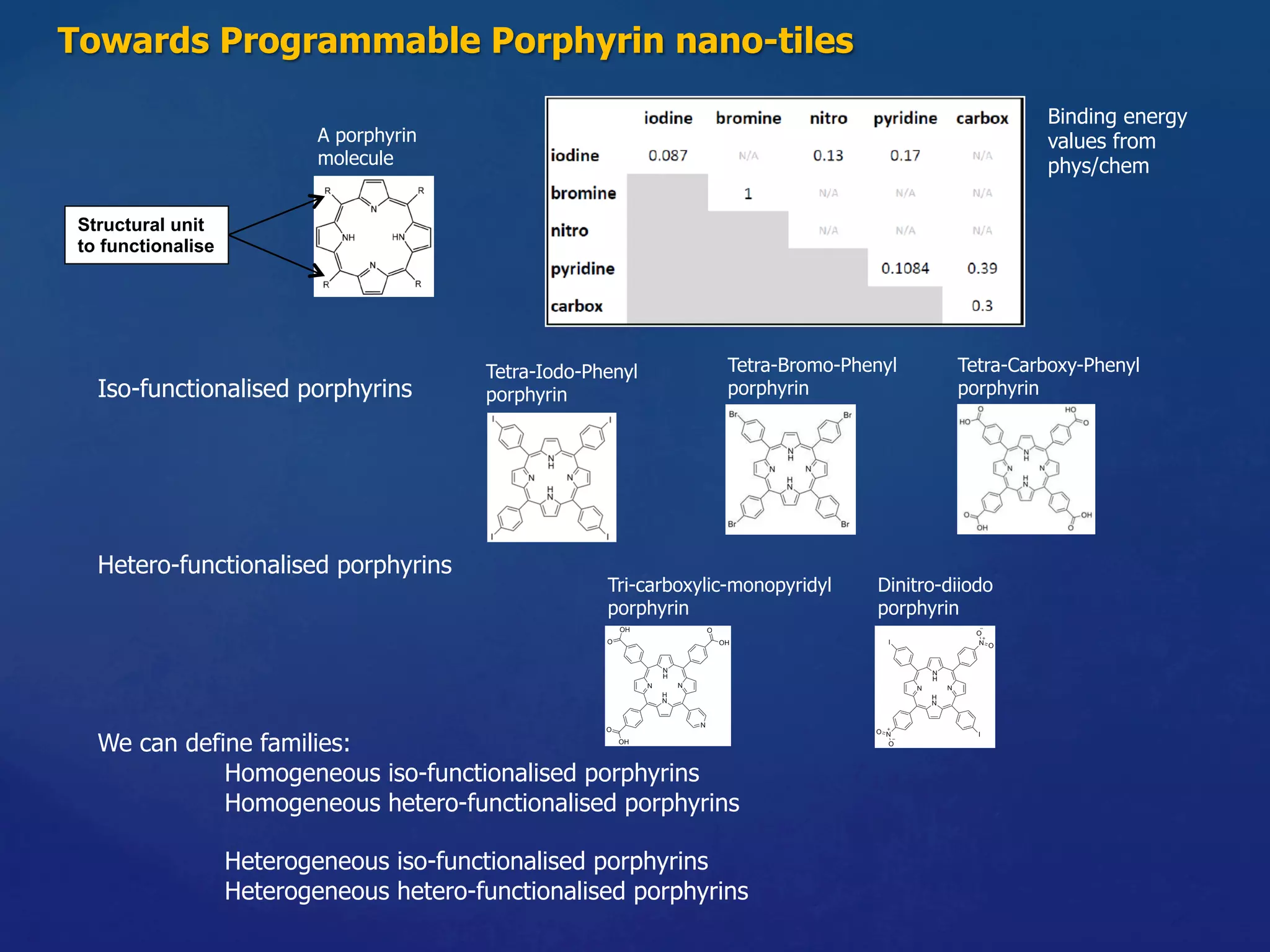
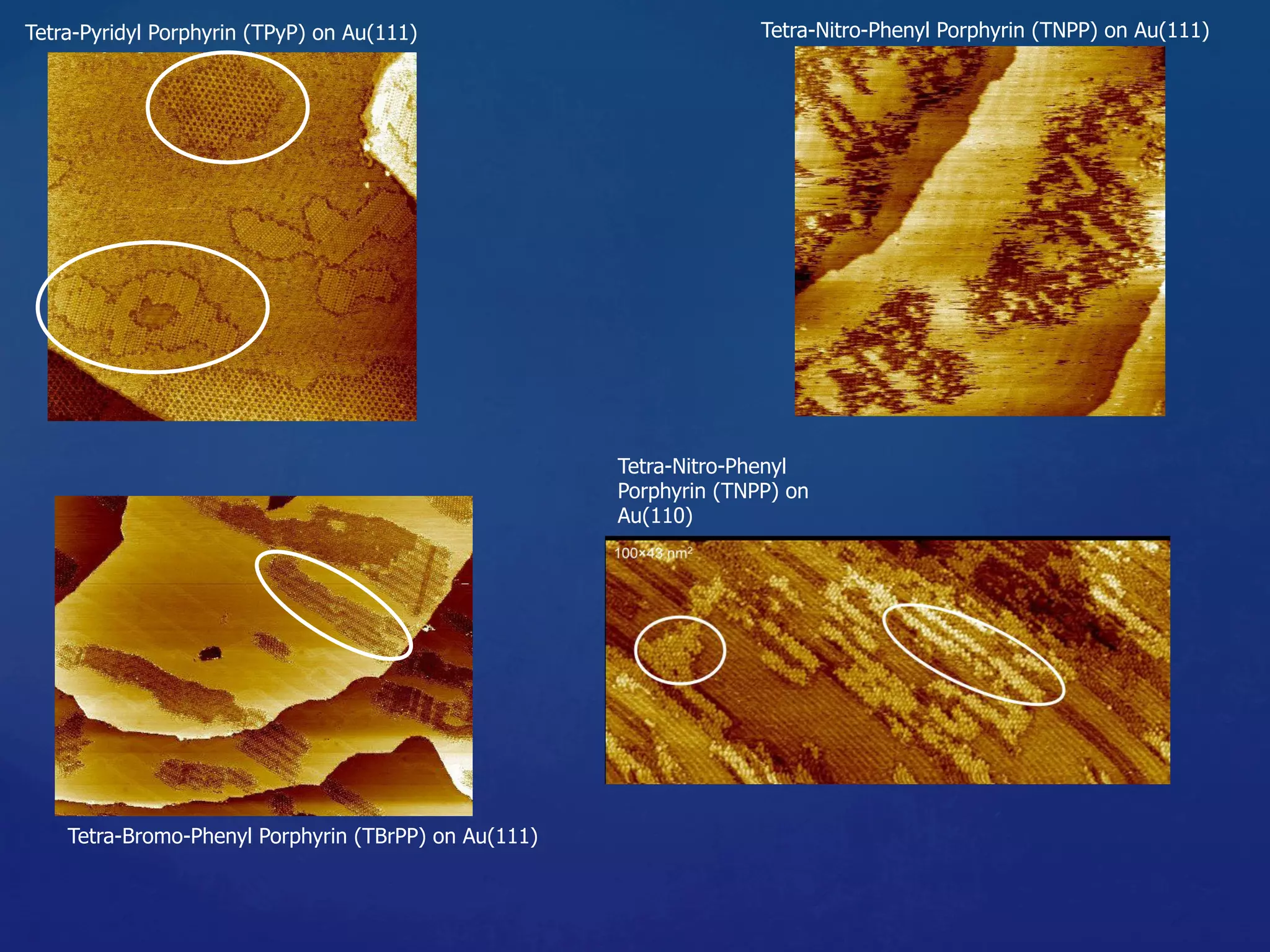
Hetero-func/onalised Porphyrin-%les Species:

25. Es = 0.5, E12 = 0.1
25
E11
E22
0.1 0.2 0.3 0.4 0.5
0.1
0.2
0.3
0.4
0.5

26. Es = 0.5, E12 = 0.5
26
E11
E22
0.1 0.2 0.3 0.4 0.5
0.1
0.2
0.3
0.4
0.5

27. Kolmogorov Complexity To The Rescue
27

28. • The string (c) 01010101...01 is not algorithmic
random (or has low K complexity) because it can be
produced by the following program:
• Program A(i):
1: n:= 0
2: Print n mod 2
3: n:= n+1
4: If n=i Goto 6
5: Goto 2
6: End
• The length of A (in bits) is an upper bound of
K(010101...01).
28

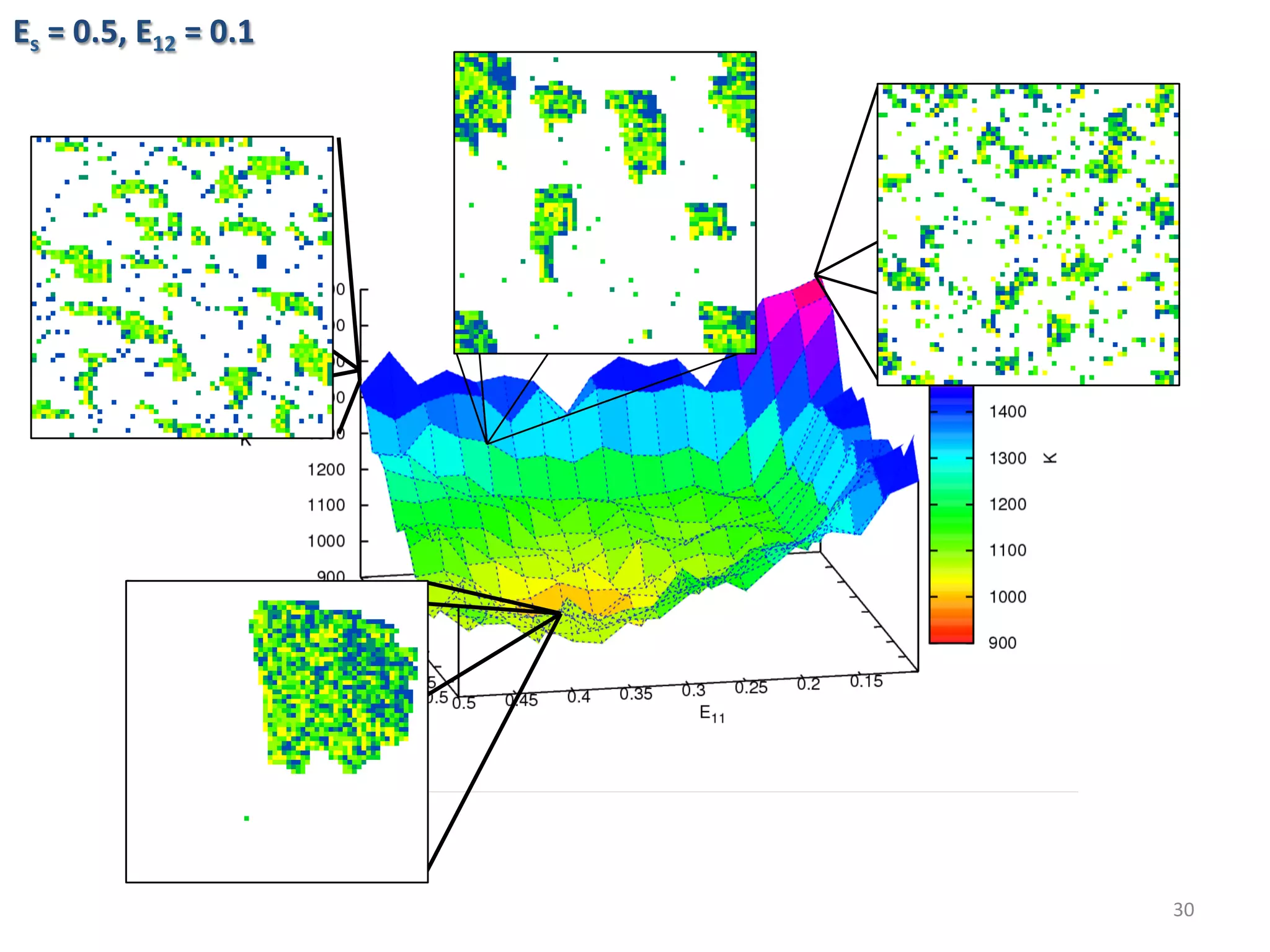
29. Algorithmic Informa6on Content
• Algorithmic Complexity of a string s, K(s),
The length of the shortest program, p, that could generate
the string.
• K is an uncomputable func6on. A prac6cal way to
approximate K is using lossless compression algorithms.
• The outputs of the simula6ons are converted into PNG
images then compressed using PNGcrush. The compressed
size of the images are the es6mated algorithmic complexity
of the outputs.
29
)})(],[Length{min()( spUpsK ==

30. Es = 0.5, E12 = 0.1
30

31. Es = 0.5, E12 = 0.5
31

32. • Complexity Measurement Based on Information Theory and Kolmogorov Complexity
LT Lui, G Terrazas, H Zenil, C Alexander, N Krasnogor. Artificial Life, 2015
Exploring programmable self-assembly in non-DNA based molecular computing, G Terrazas, H Zenil, N Krasnogor.
Natural Computing 12 (4), 499-515, 2015
• Blind optimisation problem instance classification via enhanced universal similarity metric. I Contreras, I Arnaldo, N
Krasnogor, JI Hidalgo. Memetic Computing 6 (4), 263-276, 2014.
• Is There an Optimal Level of Open-Endedness in Prebiotic Evolution? O Markovitch, D Sorek, LT Lui, D Lancet, N
Krasnogor. Origins of Life and Evolution of Biospheres 42 (5), 469-474, 2014
• Genotype-Fitness Correlation Analysis for Evolutionary Design of Self-Assembly Wang Tiles. G. Terrazas and N.
Krasnogor. In Pelta et al. editors, Studies in Computational Intelligence, v 387, NICSO 2011, pp. 73–84.
Springer-Verlag Berlin Heidelberg 2011.
• Automated Self-Assembling Programming. L. Li, P. Siepmann, J. Smaldon, G. Terrazas and N. Krasnogor. In N.
Krasnogor, S. Gustafson, D. Pelta, and J. L. Verdegay, editors, Systems Self-Assembly: Multidisciplinary
Snapshots. Elsevier 2008.
• Evolving Tiles for Automated Self-Assembly Design. G. Terrazas, M. Gheorghe, G. Kendall and N.Krasnogor. In IEEE
Congress on Evolutionary Computation, pp. 2001–2008. IEEE Press 2007.
• ProCKSI: a decision support system for protein (structure) comparison, knowledge, similarity and information.D
Barthel, J Hirst, J Błażewicz, E Burke, N Krasnogor. BMC bioinformatics 8 (1), 416, 2007.
• An Evolutionary Methodology for the Automated Design of Cellular Automaton-based Complex Systems. G. Terrazas,
P. Siepmann, G. Kendall and N. Krasnogor. Journal of Cellular Automata, 2(1):77–102, 2007, v 2, pp. 77–102.
OCP Science 2007
• Evolutionary Design for the Behaviour of Cellular Automaton-Based Complex Systems. P. Siepmann, G. Terrazas, N.
Krasnogor. In Adaptive Computing in Design and Manufacture, pp. 199–208. The Institute for People-centred
Computation 2006.
• Automated Tile Design for Self-Assembly Conformations. G. Terrazas, N. Krasnogor, G. Kendall and M. Gheorghe. In
IEEE Congress on Evolutionary Computation, v 2, pp. 1808–1814. IEEE Press, 2005.
• A Critical View of Evolutionary Design of Self-Assembly System. N. Krasnogor, G. Terrazas, D. Pelta, G. Ochoa. In
Conference on Artificial Evolution, v 3871, pp. 179–188. Springer 2005.
• Measuring the similarity of protein structures by means of the universal similarity metric. N Krasnogor, DA Pelta.
Bioinformatics 20 (7), 1015-1021, 2004
Thank you Prof. Pelta & Prof. Verdegay for
invitation and amazing hospitality!!