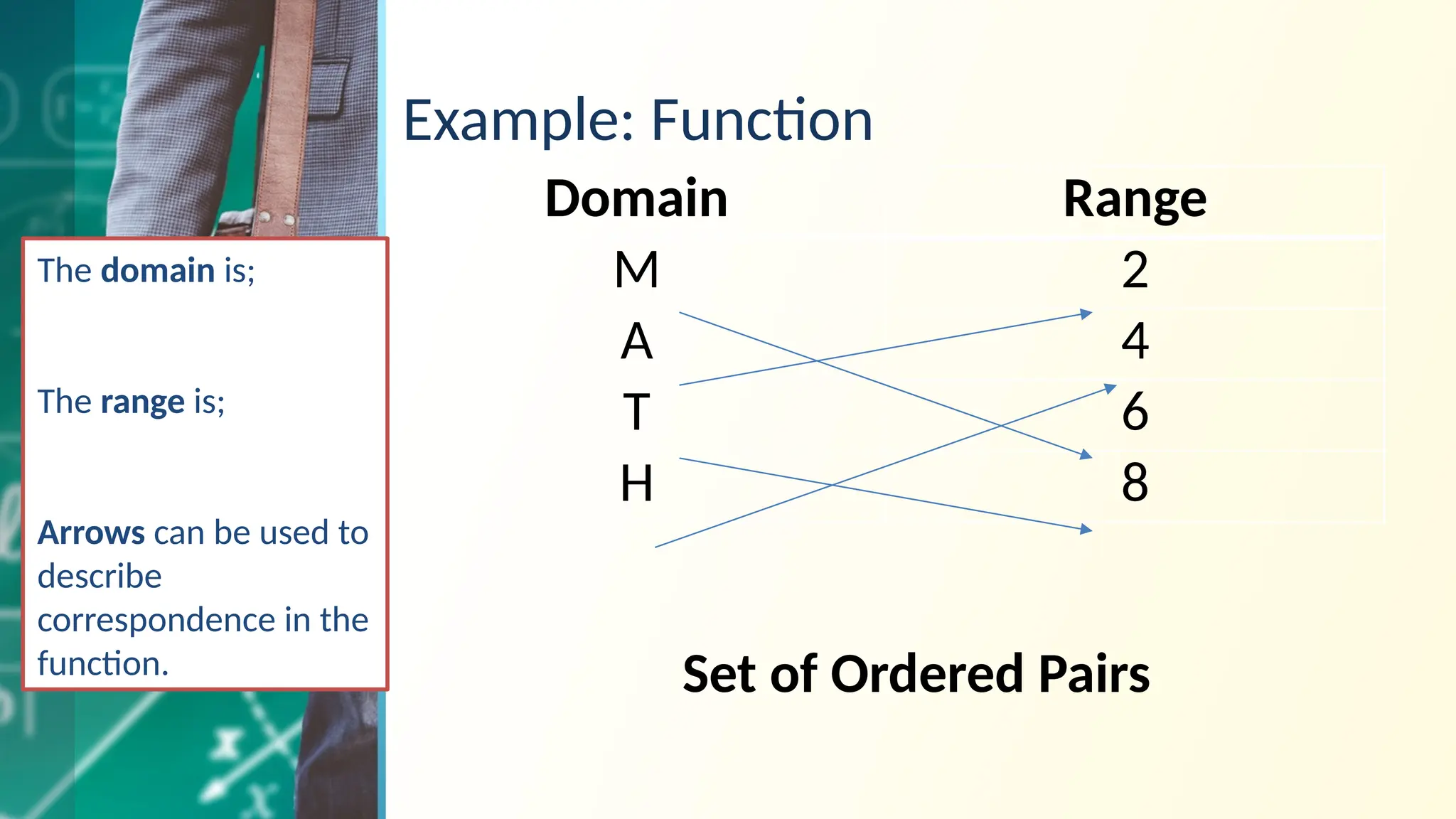
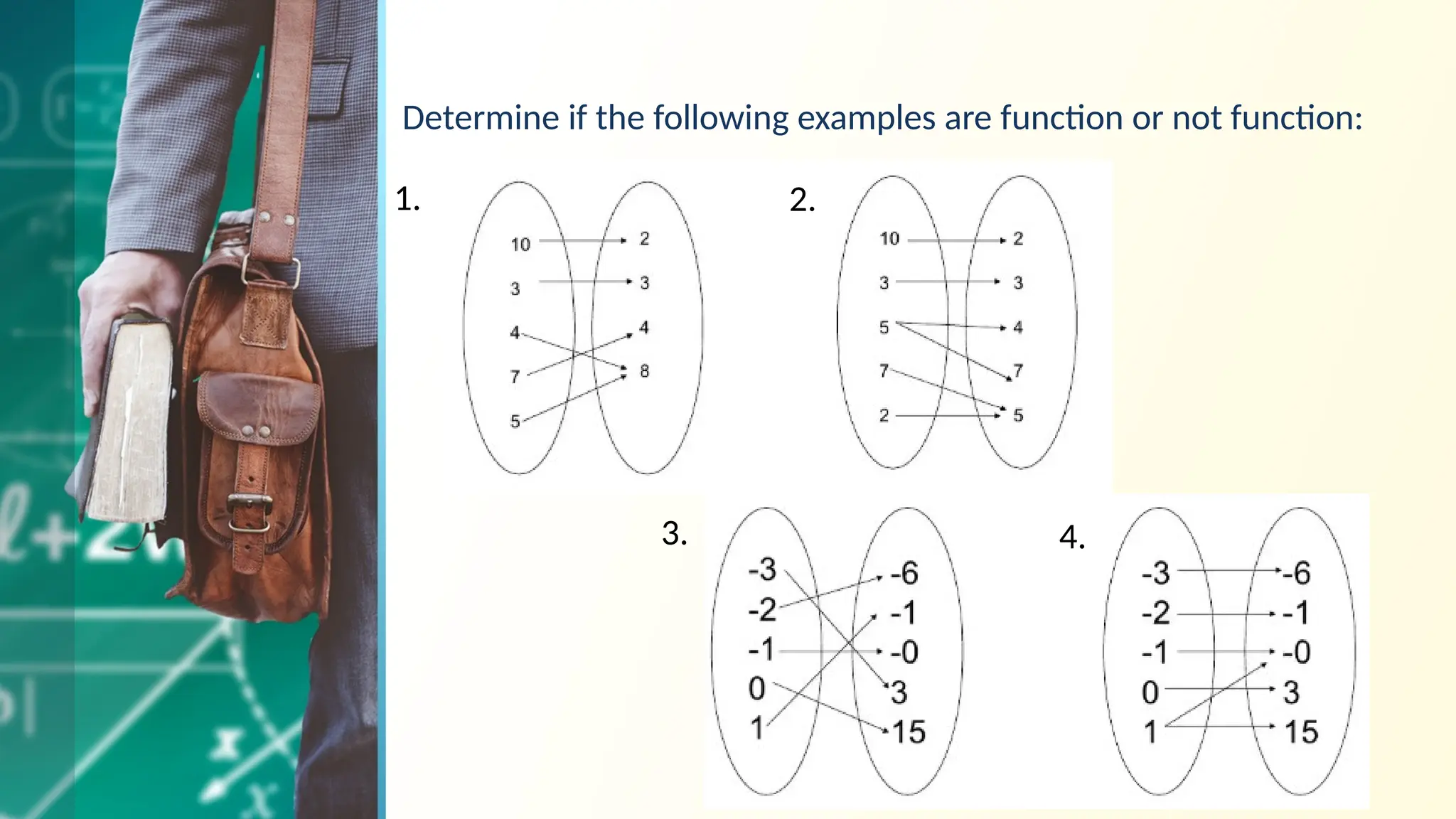
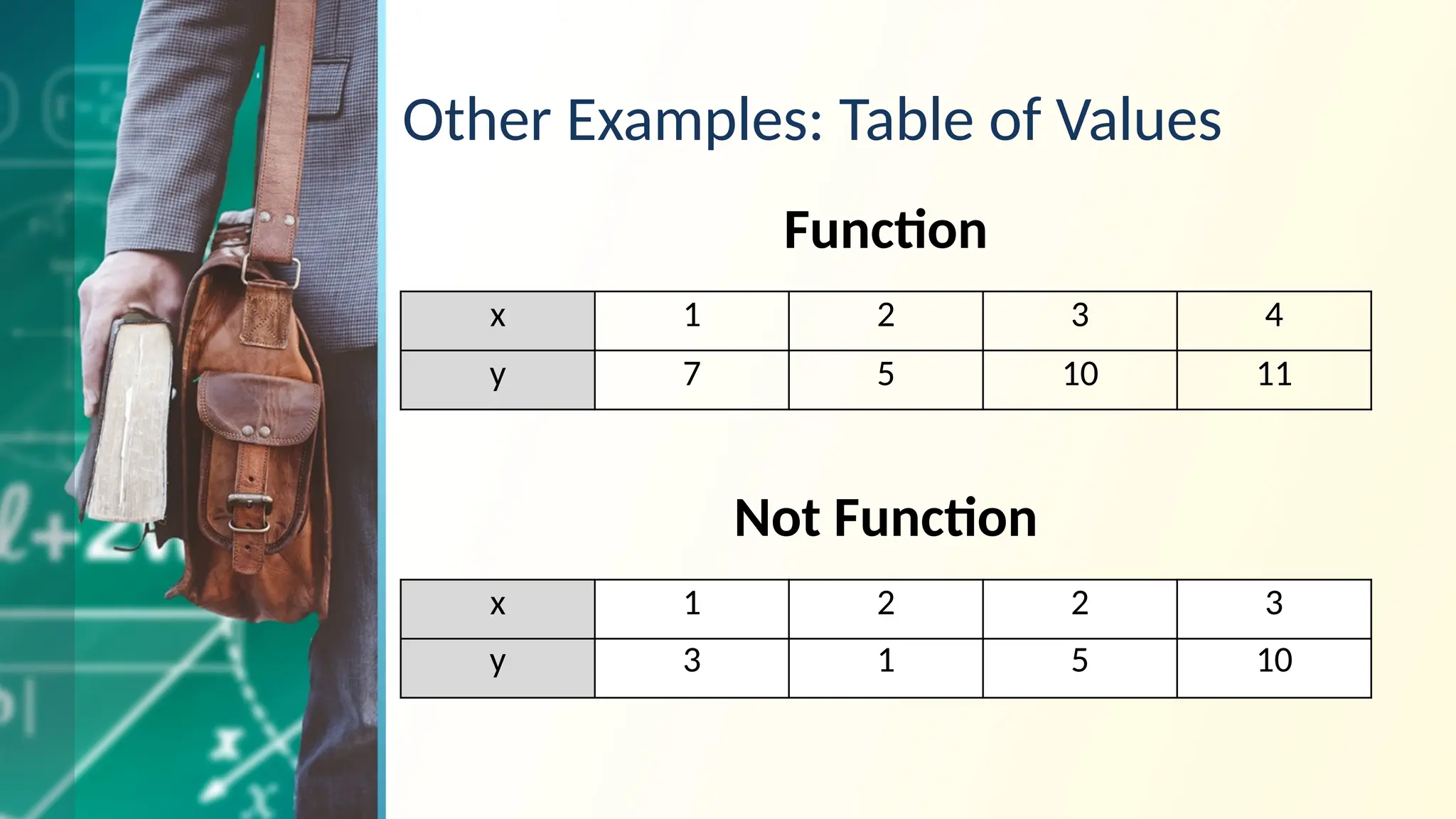
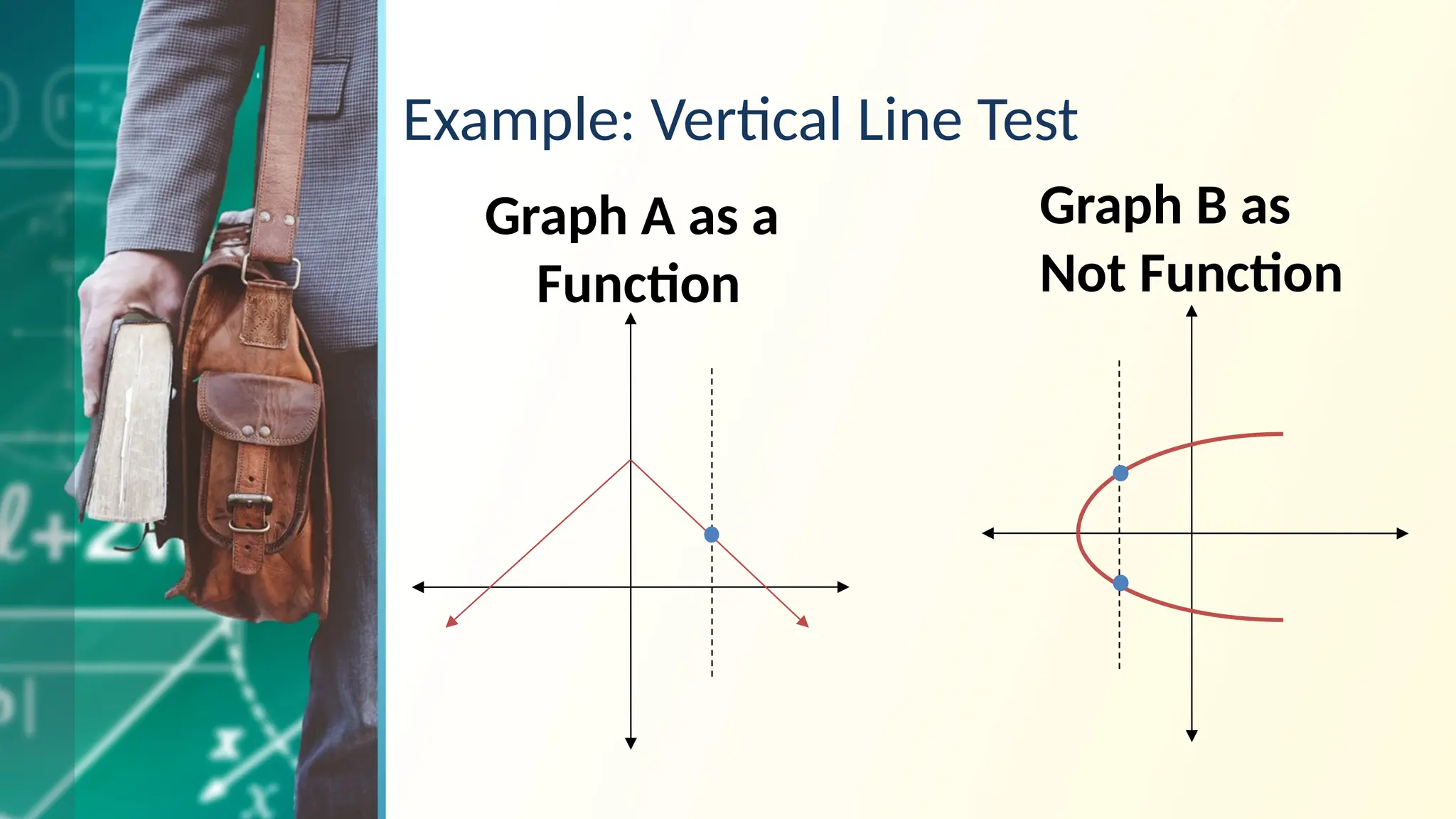
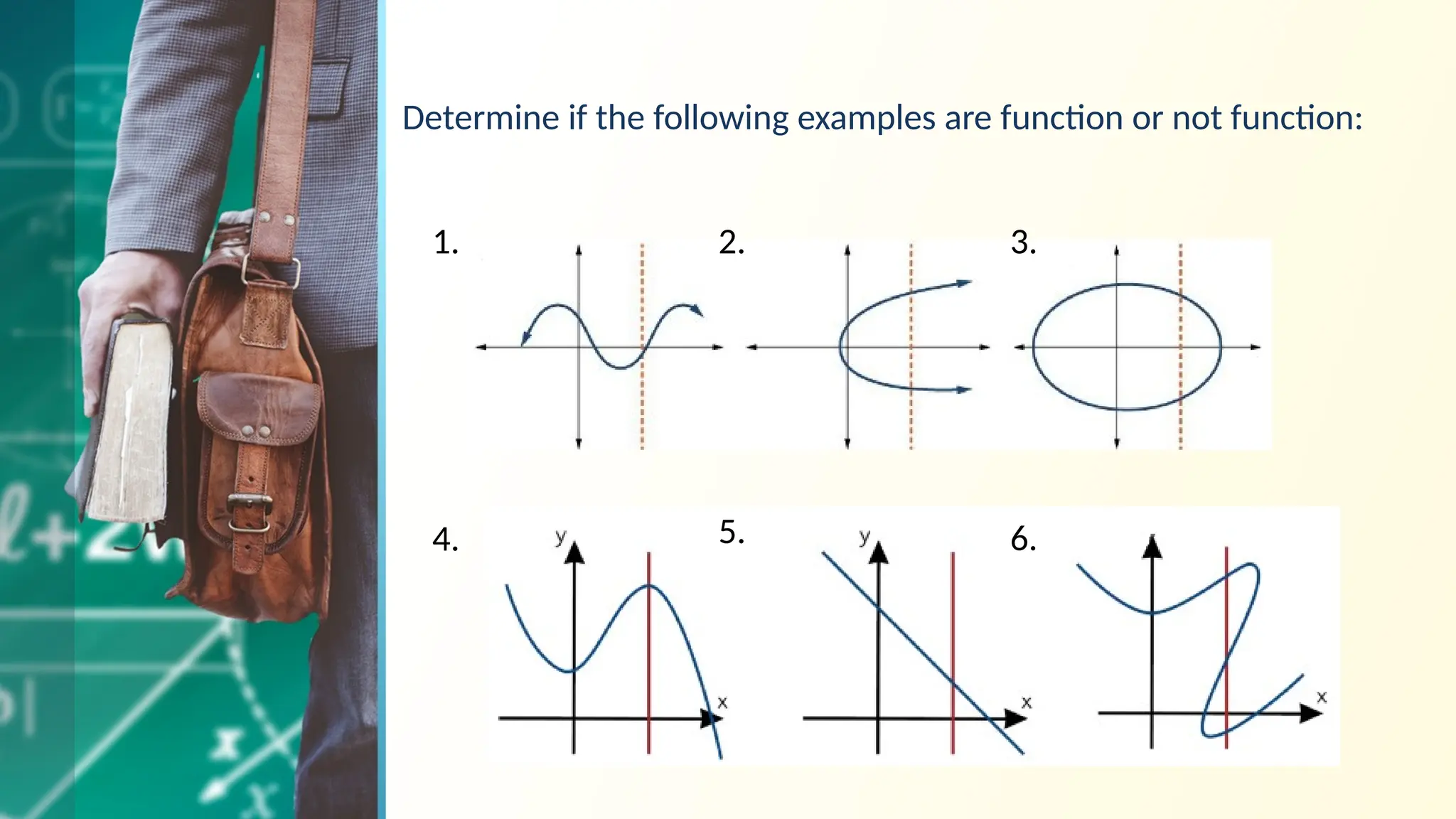
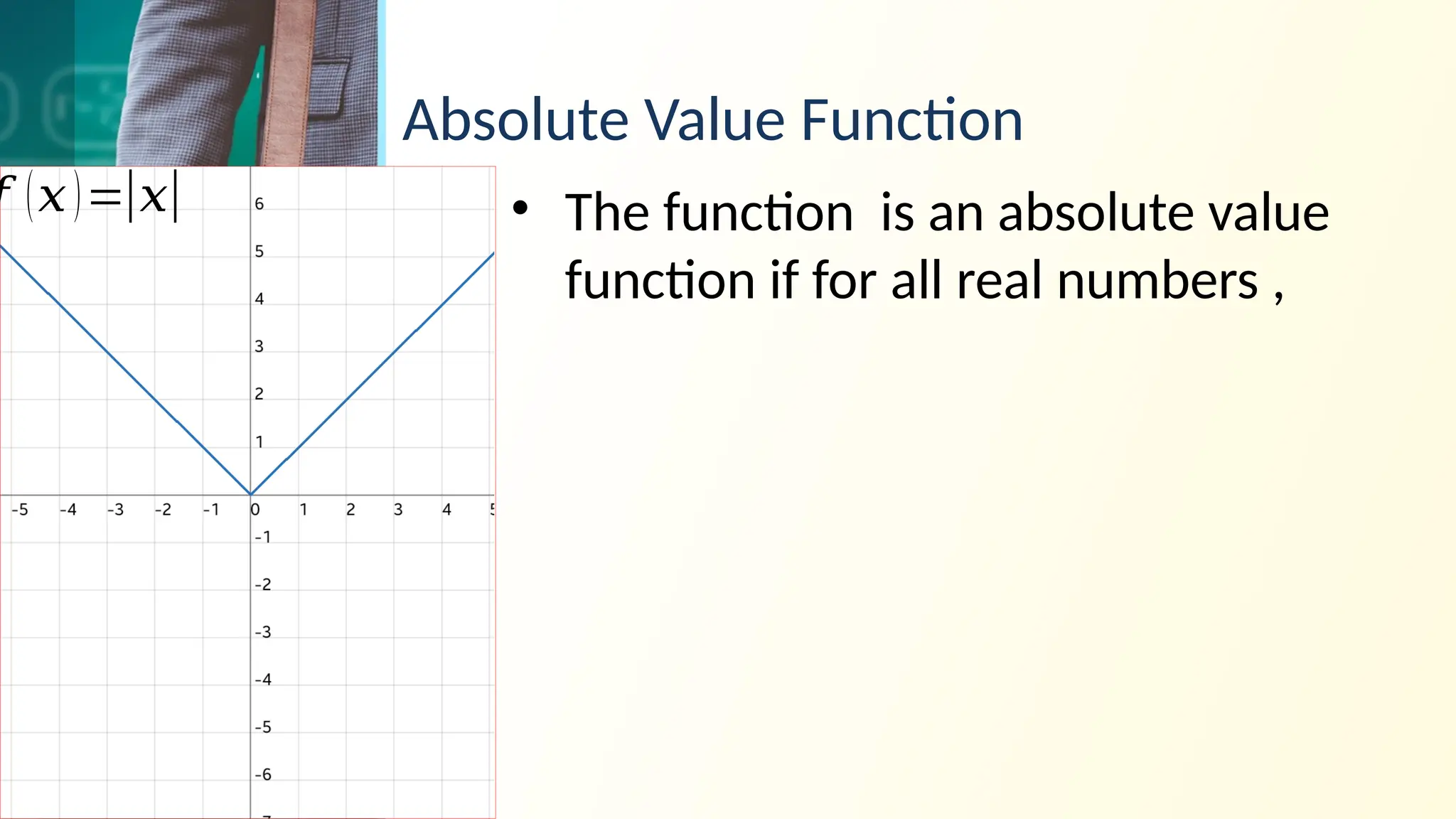
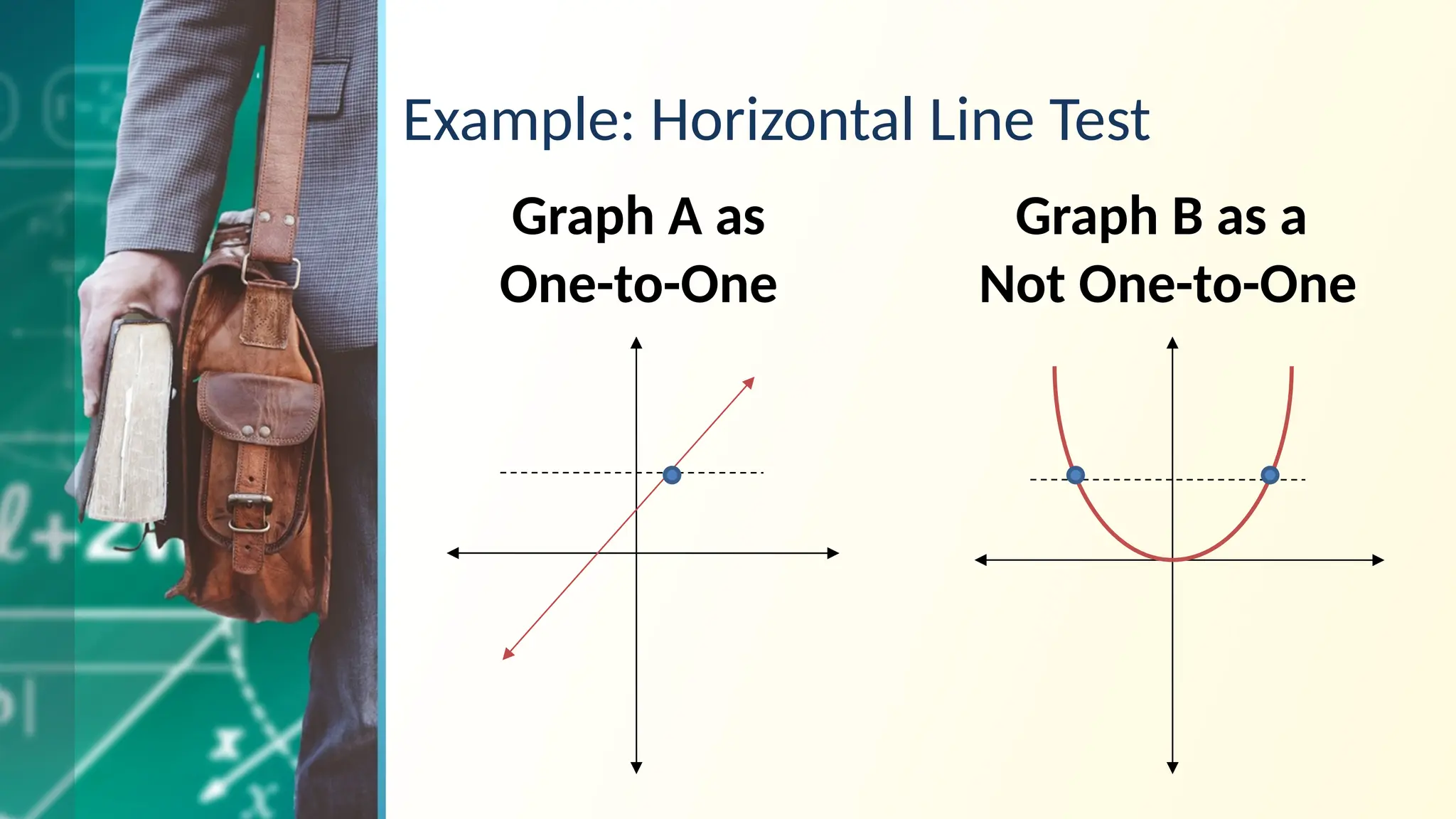
The document outlines the representation and classification of functions in general mathematics, specifically targeting concepts relevant to computer engineering. It explains relations and functions, including their domains and ranges, and discusses types of functions such as linear, quadratic, constant, identity, absolute value, piecewise, and one-to-one functions. Key tests for identifying functions, like the vertical and horizontal line tests, are also included, along with examples and objectives.

1. Representation of
Functions
General Mathematics
Ericko P. Alegria, LPT

2. Teacher: Ericko P. Alegria, LPT
Course: Bachelor of Science in Computer Engineering
Continuous Professor’s Education (CPE)
LET Passer: September 29, 2019
Major: Mathematics (secondary)

3. Objectives:
• Represent real-life situations using
functions, including piecewise function;
and
• Represent real-life situation using one-
to-one functions.

4. Relation
• A relation is a set of ordered pairs.
• The domain of a relation is the set of
first coordinates.
• The range is the set of second
coordinates.

5. Example: Relation
Letter Number
M 6
A 2
T 8
H 4
Set of Ordered Pairs
The domain is;
The range is;

6. Function
• A function is a relation in which each
element of the domain corresponds to
exactly one element of the range.
• The domain can be called inputs.
• The range can be called outputs.

7. Example: Function
Domain Range
M 2
A 4
T 6
H 8
Set of Ordered Pairs
The domain is;
The range is;
Arrows can be used to
describe
correspondence in the
function.

8. Example: Not Function
Domain Range
4 E
3 T
8 C
2 A
5 K
Domain Range
4 F
3 B
8 A
2 K
5 E
Relation H Relation I
In relation H, the
number 2 is assigned
to two letters, C and
A.
In relation I, 3 is
assigned to two
letters, F and E, and 2
is assigned to two
letters, B and A.

9. Other Examples: Mapping Diagram
1
2
3
4
2
5
10
17
Input, x Output, y
7
2
11
11
3
17
9
23
Input, x Output, y
Function Not Function

10. Determine if the following examples are function or not function:
1. 2.
3. 4.

11. Other Examples: Table of Values
x 1 2 3 4
y 7 5 10 11
x 1 2 2 3
y 3 1 5 10
Function
Not Function

12. Determine if the following examples are function or not function:
1. 2.
3. 4.

13. Other Examples: Equation
Function
Not Function

14. Determine if the following examples are function or not function:
1. 2. 3. 4.

15. Vertical Line Test
• A graph represents a function if and
only if no vertical line intersects the
graph in more one point.

16. Example: Vertical Line Test
Graph A as a
Function
Graph B as
Not Function

17. Determine if the following examples are function or not function:
6.
5.
4.
3.
2.
1.

18. Types of Function
1. Linear Function
2. Quadratic Function
3. Constant Function
4. Identity Function
5. Absolute Value Function
6. Piecewise or Compound Function
7. One-to-One Function

19. Linear Function
• A function is a linear function if ,
where and are real numbers, and
and are not both equal to zero.
𝑓 (𝑥)=3 𝑥−2

20. Quadratic Function
• A quadratic function is any
equation of the form , where , ,
and are real numbers and .
𝑓 (𝑥)=𝑥2

21. Constant Function
• A linear function is a constant
function if , where and is any real
number. Thus, .
𝑓 (𝑥)=3

22. Identity Function
• A linear function is an identity
function if , where and . thus, .
𝑓 (𝑥)=𝑥

23. Absolute Value Function
• The function is an absolute value
function if for all real numbers ,
𝑓 (𝑥)=|𝑥|

24. Piecewise or Compound Function
• A piecewise function or a
compound function is a function
defined by multiple subfunctions,
where each subfunctions applies to
a certain interval of the main
function’s domain.
𝑓 (𝑥)=
{ 2 𝑥−2,𝑖𝑓 𝑥 ≤ 1
𝑥
2
− 2𝑥+1,𝑖𝑓 𝑥>1

25. One-to-One Function
• A one-to-one function is a function in
which for each value of in the range
of , there is just one value in the
domain of such that .
• In other words, is one-to-one if
implies .

26. Example: One-to-One Function
f
1 5
2
g
1 5
2 7
Not One-to-One One-to-One
(a) (b)
In (a), there are two
values in the domain
that are both mapped
onto 5 in the range.
Hence, the function is
not one-to-one.
In (b), for each output
in the range of , there
is only one input in
the domain that gets
mapped onto it. Thus,
is a one-to-one
function.

27. Horizontal Line Test
• a function is one-to-one if no
horizontal line intersects its graph more
than once.

28. Example: Horizontal Line Test
Graph A as
One-to-One
Graph B as a
Not One-to-One

29. Next Lesson:
• Chapter 1, Lesson 1.2:
Evaluation of Functions

30. Reference:
• Oronce, Orlando A. General
Mathematics: First Edition. Rex
Bookstore, Inc., 2016

31. Thank
You!