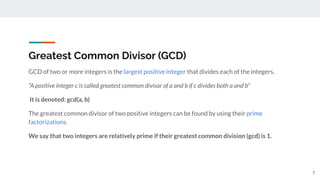
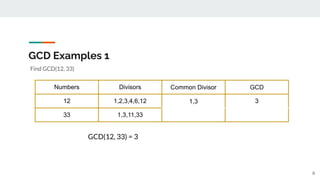
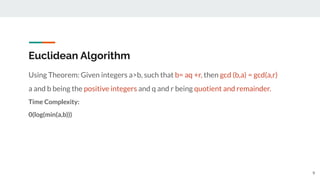
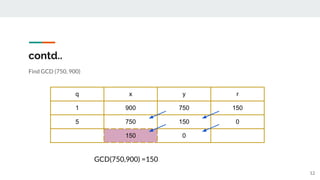
This document introduces number theory and the greatest common divisor (GCD). It defines key concepts like prime numbers, division, and the Euclidean algorithm for finding the GCD. The Euclidean algorithm uses the fact that the GCD of two numbers a and b is equal to the GCD of b and the remainder of a divided by b. The document provides examples of using the Euclidean algorithm and method 1 (repeated division) and method 2 (working backwards from the definitions) to find the GCD of numbers like 12 and 33. It concludes with applications of GCD in fields like computer organization, coding, and cryptography.

1. Introduction to Number Theory
and
Greatest Common Divisor
By Rashila Shrestha
MTech. IT 2021
Kathmandu University
Sept 14, 2022

2. Outline
❏ Number Theory
❏ Greatest Common Divison (GCD)
❏ Euclidean Algorithm
❏ Solving GCD using method 1 and 2
❏ Applications
2

3. 3

4. Number Theory
Field of Mathematics consisting of study of properties of whole number.
Integers and their properties
Uses computers in factoring large integers, determining primes, testing conjectures and
solving problems.
Key ideas in number theory include divisibility and primal of integers
4

5. Division
Definition: If a and b are integers with a ≠ 0, then a divides b if there exists
an integer c such that b = ac.
When a divides b we say that a is a factor or divisor of b and that b is a
multiple of a.
The notation a | b denotes that a divides b.
If a | b, then b/a is an integer.
If a does not divide b, we write a ∤ b.
5

6. Primes
Definition: A positive integer p greater than 1 is called prime if the only
positive factors of p are 1 and p.
A positive integer that is greater than 1 and is not prime is called
composite.
Example: The integer 7 is prime because its only positive factors are 1
and 7, but 9 is composite because it is divisible by 3.
6

7. Greatest Common Divisor (GCD)
GCD of two or more integers is the largest positive integer that divides each of the integers.
“A positive integer c is called greatest common divisor of a and b if c divides both a and b”
It is denoted: gcd(a, b)
The greatest common divisor of two positive integers can be found by using their prime
factorizations.
We say that two integers are relatively prime if their greatest common division (gcd) is 1.
7

8. GCD Examples 1
Find GCD(12, 33)
Numbers Divisors Common Divisor GCD
12 1,2,3,4,6,12 1,3 3
33 1,3,11,33
GCD(12, 33) = 3
8

9. Euclidean Algorithm
Using Theorem: Given integers a>b, such that b= aq +r, then gcd (b,a) = gcd(a,r)
a and b being the positive integers and q and r being quotient and remainder.
Time Complexity:
0(log(min(a,b)))
9

10. GCD contd..
Euclid’s Algorithm to calculate GCD in pseudocode:
function gcd(x, y)
while (y ≠ 0)
r = x mod y;
x = y
y = r
return x
10

11. Finding GCD using Euclid’s Algorithm (Method 1)
Find GCD(12, 33)
q x y r
2 33 12 9
1 12 9 3
3 9 3 0
3 0
GCD(12,33) = 3
11

12. contd..
Find GCD (750, 900)
q x y r
1 900 750 150
5 750 150 0
150 0
GCD(750,900) =150
12

13. Finding GCD using Euclid’s Algorithm(Method 2)
By definition:
x=yq+r such that x>y then gcd(x,y) = gcd(y,r)
● 33 = 12 x 2 +9
● 12 = 9 x 1 +3
● 9 = 3 x 3 +0
(since gcd(x,y) = gcd(y, x mod y))
gcd(33,12) = gcd(12,9) = gcd(9,3) =3
Therefore, gcd(12,33) = 3
13
Find GCD(12,33)
Stopping Condition

14. Applications
Computer Organization and Security
Coding and Cryptography(Encryption Algorithm RSA))
Random Number Generation
Hash Functions and Graphics
14

15. References
1. Intro to Algorithms: CHAPTER 33: NUMBER-THEORETIC ALGORITHMS (ustc.edu.cn)
2. https://primes.utm.edu/notes/faq/one.html
3. number theory | Definition, Topics, & History | Britannica
15

16. Thank You
Any Queries??
16