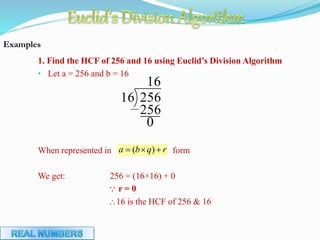
This document discusses the Euclid's algorithm for finding the greatest common divisor (GCD) of two numbers. It begins by explaining the algorithm and providing an example of finding the GCD of 256 and 16. Then it provides 3 additional examples of using the algorithm to find the GCD of various number pairs. The last part asks the reader to find the largest number that divides two given numbers and leaves specific remainders. It walks through applying the Euclid's algorithm to solve this problem.

1. DONE BY ,
HARISH R KULKARNI
NIKHIL SAI RAM
SAMARTH KL “X” B
RISHABH YADAV
PREM CHULAKI

3. Greatest Common Divisor / Highest Common Factor (HCF)
Example: HCF for 2 & 8 = 2
• For two positive integers a & b where a > b , they can be expressed as
• Where 0 ≤ r < b & q € Ẕ .If “r = 0” then “b” is the HCF/GCD of “a & b”
• If “r ≠ 0” then apply Euclid’sdivision lemma to b and r.
• For some integers m and n , 0 ≤ n < r
• Continue this process till the remainder is zero.
• The divisor which gives you the remainder as 0 is your HCF/GCD
rqba  )(
nmrb  )(

4. 1. Find the HCF of 256 and 16 using Euclid’s Division Algorithm
• Let a = 256 and b = 16
When represented in form
We get: 256 = (16×16) + 0
 r = 0
16 is the HCF of 256 & 16
Examples
16
0
256
25616
rqba  )(

5. 2. Find the HCF of 13 and 24 using Euclid’s Division Algorithm
Let, a = 24 and b = 13
 “r ≠ 0” Again “r ≠ 0”
New dividend and divisor are  New dividend and divisor are 2 and 1
13 and 11 respectively
Again,  “r ≠ 0” r = 0,  HCF of 13 & 24 is 1
New dividend and divisor are
11 and 2 respectively
1
11
13
2413
5
1
10
112
1
2
11
1311
2
0
2
21

6. 3. Find the HCF of 1424 and 3084 using Euclid’s Division Algorithm
Let, a = 3084 and b = 1424 .
 “r ≠ 0” Again “r ≠ 0”
New dividend and divisor are  New dividend and divisor are 8 and 4.
1424 and 236 respectively.
Again,  “r ≠ 0” r = 0,  HCF of 1424 & 3084 is 4.
New dividend and divisor are
236 and 8 respectively.
6
8
1416
1424236
2
236
2848
30841424
29
4
232
2368
2
0
8
84

7. 4. Find the largest number that divides 2623 & 2011 and leaves
Remainders 5 & 9 respectively
Point to remember
2 divides 25 leaving a remainder =1
Also,  2 divides 24 completely leaving a remainder = 0
24 = 25 – 1
Same logic has to be applied for this question
 2623 & 2011 when divided leaves remainders of 5 & 9
We have to find HFC of 2623 – 5 = 2618 and 2011 – 9 = 2002,
so we consider the numbers 2618 & 2002.
2618 = 2002 × 1 + 616
Now applying Euclid’s lemma to 2618 & 2002 we get,
As r ≠ 0 we again apply Euclid’s lemma to 2002 & 616.

8. 616 = 154 × 4 + 0
Now, Remainder (r) = 0
Hence, the required number is 154
We have 2002 = 616 × 3 + 154 as again we see that r ≠ 0.
Applying Euclid’s lemma again to 616 and 154 we get,
Hence, according to the algorithm the divisor = HCF/GCD
∴ 154 = HCF of 2618 and 2002

9. 1. Arranging the terms in the given question as per the Euclid’s
Division Lemma
2. Identification of the Dividend, Divisor, Quotient and Remainder .
3. Any positive integer can be represented as ‘2q’ or ‘2q+1’.
4. Even number × Any Number = Even number .
5. Even number × Any Number + Odd number = Odd number .
a = b × q + r
REVISION
General equation