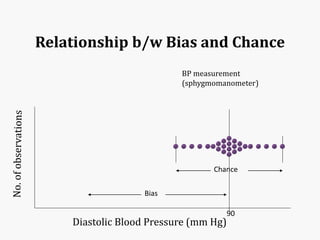
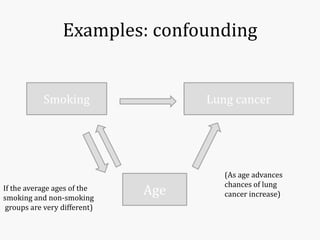
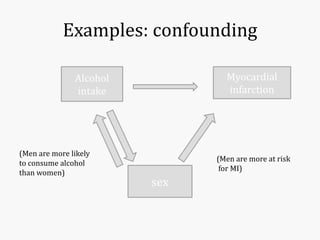
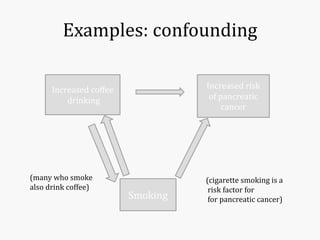
Systematic and random errors can affect epidemiological studies. Random errors are due to chance and include individual biological variation, measurement error, and sampling error. Systematic errors, also called biases, are non-random and can distort study results. Selection bias occurs if study groups differ in characteristics unrelated to exposure that influence outcomes. Measurement bias happens if exposures or diseases are inaccurately classified. Confounding is present when a third factor is associated with both the exposure and outcome under investigation. Careful study design and analysis techniques can help reduce biases and errors to obtain more accurate results.

1. Error, Bias and Confounding
Presenter: Dr. Mitasha Singh
Moderator: Dr. SK Raina
30.10.15

2. Error- Definitions
• A false or mistaken result obtained in a study or
experiment
• Random error is the portion of variation in
measurement that has no apparent connection to
any other measurement or variable, generally
regarded as due to chance
• Systematic error which often has a recognizable
source, e.g., a faulty measuring instrument, or
pattern, e.g., it is consistently wrong in a particular
direction
(Last)

3. Random error
• Divergence on the basis of chance alone of an
observation on a sample from the population
from the true population values
• ‘random’ because on an average it is as likely to
result in observed values being on one side of
the true value as on the other side
• Inherent in all observations
• Can be minimized, but never avoided altogether

4. Sources of random error
1. Individual biological variation
2. Measurement error
3. Sampling error

5. Measurement error
• errors in measuring exposure or disease
• Examples-
o Blood Pressure measurement- estimates show that
approximately 1/3rd of its observed variability is due to measurement
error.
o Nutrient instruments- food records, 24 hour recalls and
biomarkers
o Environment risk factors- laboratory and device error
o Hormone levels- lab error
o Tape incorrectly fixed to height board
o Scale consistently reads low by 0.5 kg
o Failure to remove heavy clothing before weighing
o Misleading questions

6. Sampling error
• Since inclusion of individuals in a sample is
determined by chance, the results of analysis
on two or more samples will differ purely by
chance. (Last)
• Influenced by:
– Sample size (Greater with smaller sample sizes)
– Sampling scheme

7. Assessing the role of chance
1. Hypothesis testing
2. Estimation

8. Hypothesis testing
• Start off with the Null Hypothesis (H0)
• the statistical hypothesis that one variable has
no association with another variable or set of
variables, or that two or more population
distributions do not differ from one another
• the null hypothesis states that the results
observed in a study, experiment or test are no
different from what might have occurred as a
result of operation of chance alone
(Last)

9. Statistical tests – errors
Null hypothesis (Ho)
(H0) false (H0) true
CONCLUSION
OF
STATISTICAL
TEST
SIGNIFICANT
(H0) Rejected
NOT
SIGNIFICANT
(H0) Accepted
Type I
( α ) error
Type II
( β ) error
Power
Fletcher

10. Statistical tests - errors
• Type I (α) error: error of rejecting a true null
hypothesis , i.e. declaring a difference exists
when it does not
• Type II (β) error: error of failing to reject a false
null hypothesis , i.e. declaring that a difference
does not exist when in fact it does
• Power of a study: ability of a study to
demonstrate an association if one exists
Power = 1- β

11. Estimation
• Effect size observed in a particular study is
called ‘Point estimate’
• True effect is unlikely to be exactly that
observed in study because of random variation
• Confidence interval (CI): interval computed
with a given probability e.g. 95%, that the true
value such as a mean, proportion, or rate is
contained within the interval

12. Confidence intervals
If the study is unbiased, there is a 95% chance that
that the interval includes the true effect size. The
true value is likely to be close to the point estimate,
less likely to be near the outer limits of that
interval, and could (5 times out of 100) fall outside
these limits altogether.
Fletcher

13. Precision
Precision in epidemiologic measurements
corresponds to the reduction of random error.
Rothman. Modern Epidemiology. 1986.

14. Dealing with error
• Increasing the sample size: sample size depends
upon
- level of statistical significance (α error)
- Acceptable chance of missing a real effect (β error)
- Magnitude of effect under investigation
- Amount of disease in population
- Relative sizes of groups being compared
• Systematic quality control procedures to reduce
measurement error.

15. Bias
• Deviation of results or inferences from the truth, or
processes leading to such deviation. Any trend in
the collection, analysis, interpretation, publication,
or review of data that can lead to conclusions that
are systematically different from the truth.
(Last)
• A process at any stage of inference tending to
produce results that depart systematically from
true values. (Fletcher)

16. Relationship b/w Bias and Chance
Chance
Bias
Diastolic Blood Pressure (mm Hg)
90
BP measurement
(sphygmomanometer)

17. Types of biases
1. Selection bias
2. Measurement / (mis)classification bias

18. Selection bias
• Errors due to systematic differences in
characteristics between those who are selected for
study and those who are not.
(Last; Beaglehole)
• When comparisons are made between groups of
patients that differ in ways other than the main
factors under study, that affect the outcome under
study. (Fletcher)

19. Examples of Selection bias
• Subjects: hospital cases under the care of a
physician
• Excluded:
1. Die before admission – acute/severe disease.
2. Not sick enough to require hospital care
3. Do not have access due to cost, distance etc.
• Result: conclusions cannot be generalized
(Last)

20. Examples: selection bias
• Respondents to study on ‘effects of smoking’ usually
are not as heavy smokers as non-respondents hence
they volunteer either because they are unwell, or
worried about an exposure
• In a cohort study of newborn children, the
proportion successfully followed up for 12 months
varied according to the income level of the parents

21. Example: selection bias
• Question: association b/w formaldehyde
exposure and eye irritation
• Subjects: factory workers exposed to
formaldehyde
• Bias: those who suffer most from eye irritation
are likely to leave the job at their own request
or on medical advice
• Result: remaining workers are less affected;
association effect is diluted

22. Measurement bias
• Systematic error arising from inaccurate
measurements (or classification) of subjects or
study variables. (Last)
• Occurs when individual measurements or
classifications of disease or exposure are
inaccurate (i.e. they do not measure correctly what
they are supposed to measure)
(Beaglehole)
• If patients in one group stand a better chance of
having their outcomes detected than those in
another group.
(Fletcher)

23. Example: Measurement bias
Theoretical definition
• Exposure: passive
smoking – inhalation of
tobacco smoke from
other people’s smoking
• Disease: Myocardial
infarction – necrosis of
the heart muscle tissue
Empirical definition
• Exposure: passive
smoking – time spent
with smokers (having
smokers as room-
mates)
• Disease: Myocardial
infarction – certain
diagnostic criteria
(chest pain, enzyme
levels, signs on ECG)

24. Example: measurement bias
• analysis of Hb by different methods
(cyanmethemoglobin and Sahli's) in cases and
controls.
• biochemical analysis of the two groups from two
different laboratories, which give consistently
different results

25. Example: measurement bias
• patients suffering from MI are more likely to
recall and report ‘lack of exercise’ in the past
than controls. (differences in accuracy or completeness of
recall to memory of past events or experience.)
• Use of information taken from medical records
to determine if women on birth control pills
were at greater risk for thromboembolism than
those not on pill. (women with thrombophlebitis, if aware of
association b/w estrogens and thrombotic events, might report
use of ocp more completely than women without phlebitis)

26. Accuracy
The degree to which a measurement, or an
estimate based on measurements, represents
the true value of the attribute that is being
measured.
Last. A Dictionary of Epidemiology. 1988

27. Methods for controlling Selection Bias
During Study Design
1. Randomization
2. Restriction
3. Matching
During analysis
1. Stratification
2. Adjustment

28. Dealing with measurement bias
1. Blinding
- Subject
- Observer / interviewer
- Analyser
2. Strict definition / standard definition for
exposure / disease / outcome
3. Equal efforts to discover events equally in
all the groups

29. Confounding
1. A situation in which the effects of two processes are not
separated. The distortion of the apparent effect of an
exposure on risk brought about by the association with
other factors that can influence the outcome
2. A relationship b/w the effects of two or more causal
factors as observed in a set of data such that it is not
logically possible to separate the contribution that any
single causal factor has made to an effect
(Last)

30. Confounder … must be
1. Risk factor among the unexposed (itself a
determinant of disease)
2. Associated with the exposure under study
3. Unequally distributed among the exposed and
the unexposed groups

31. Examples: confounding
Smoking Lung cancer
AgeIf the average ages of the
smoking and non-smoking
groups are very different)
(As age advances
chances of lung
cancer increase)

32. Examples: confounding
Alcohol
intake
Myocardial
infarction
sex
(Men are more likely
to consume alcohol
than women)
(Men are more at risk
for MI)

33. Examples: confounding
Increased coffee
drinking
Increased risk
of pancreatic
cancer
Smoking
(many who smoke
also drink coffee)
(cigarette smoking is a
risk factor for
for pancreatic cancer)

34. Example: multiple biases
• Study: Association b/w regular exercise and risk of
CHD
• Methodology: employees of a plant offered an
exercise program; some volunteered, others did not
coronary events detected by regular voluntary
check-ups, including a careful history, ECG,
checking routine heath records
• Result: the group that exercised had lower CHD
rates

35. Example
• Selection: volunteers might have had initial lower
risk (e.g. lower lipids etc.)
• Measurement: exercise group had a better chance
of having a coronary event detected since more
likely to be examined more frequently
• Confounding: if exercise group smoked cigarettes
less, a known risk factor for CHD

36. Methods for controlling Confounders
During Study Design
1. Randomization
2. Restriction
3. Matching
During analysis
1. Stratification
2. Statistical modelling

37. Bias
• Systematic
• Is due to mistakes which
can be avoided at the
planning stage of study
• Control and prevention
requires careful attention
Error
• Random
• Never be completely
avoided
• Can be controlled by
selecting appropriate
sample size, sampling
method and precise
measurements.

38. Thank you