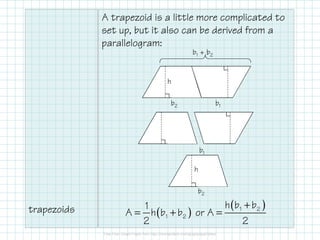
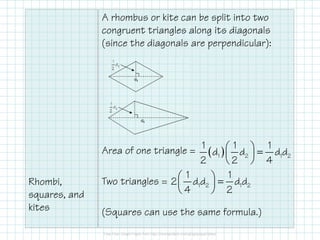
The document discusses formulas for calculating the areas of various shapes including triangles, quadrilaterals, parallelograms, trapezoids, rhombi, squares, and kites. It provides the area formulas, explains how to derive the formulas for parallelograms, triangles, and trapezoids from rectangles, and includes examples of using the formulas to calculate heights and areas.

1. Obj. 29 Area Formulas
The student is able to (I can):
• Develop and use formulas for finding the areas of
triangles and quadrilaterals

2. area
The number of square units that will
completely cover a shape without
overlapping
rectangle area One of the first area formulas you have
formula
learned was for a rectangle: A = bh, where
b is the length of the base of the rectangle
and h is the height of the rectangle.
h
A = bh
b

3. We can take any parallelogram and make a
rectangle out of it:
parallelograms
The area formula of a parallelogram is the
same as the rectangle: A = bh
(Note: The main difference between these
formulas is that for a rectangle, the height
is the same as the length of a side; a
parallelogram’s side is not necessarily the
same as its height.)

4. Example
Find the height and area of the
parallelogram.
18
10
h
6
We can use the Pythagorean Theorem to
find the height:
h = 102 − 62 = 8
Now that we know the height, we can use
the area formula:
A = ( 18 )( 8 ) = 144 sq. units

5. We can use a similar process to find out
that the area of a triangle is one-half that
of a parallelogram with the same height
and base:
triangles
1
bh
A = bh or A =
2
2

6. A trapezoid is a little more complicated to
set up, but it also can be derived from a
parallelogram:
b1 + b2
h
b2
b1
b1
h
b2
trapezoids
h (b1 + b2 )
1
A = h ( b 1 + b2 ) or A =
2
2

7. A rhombus or kite can be split into two
congruent triangles along its diagonals
(since the diagonals are perpendicular):
Rhombi,
squares, and
kites

Area of one triangle = 1 ( d1 )  1 d2  = 1 d1d2

2
2  4
1
 1
Two triangles = 2  d1d2  = d1d2

4
 2
(Squares can use the same formula.)

8. Example
Find the d2 of a kite in which d1 = 12 in. and
the area = 96 in2.
d1d2
A=
2
12d2
96 =
2
12d2 = 192
d2 = 16 in.