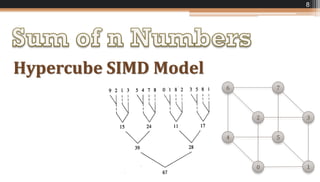
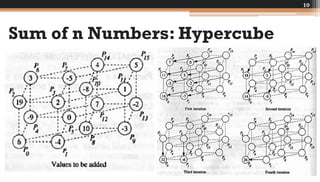
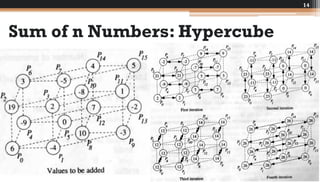
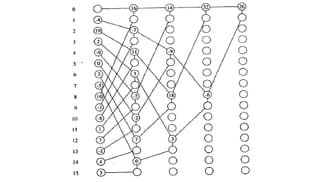
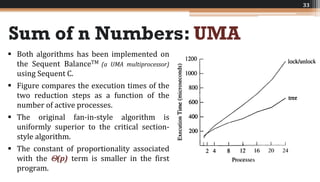
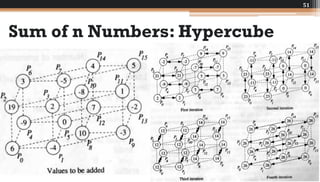
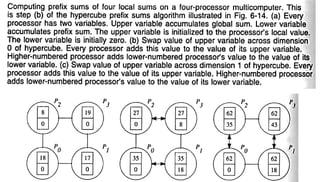
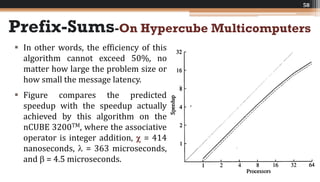
The document discusses various parallel computing algorithms, focusing on data parallelism and control parallelism, particularly in relation to summation operations. It details cost-optimal algorithms, their implementation on different architectures, and emphasizes the importance of minimizing communication steps for efficiency. Additionally, it presents design strategies that advocate for data-parallel approaches before resorting to control-parallel solutions due to their greater ease of implementation and scalability.