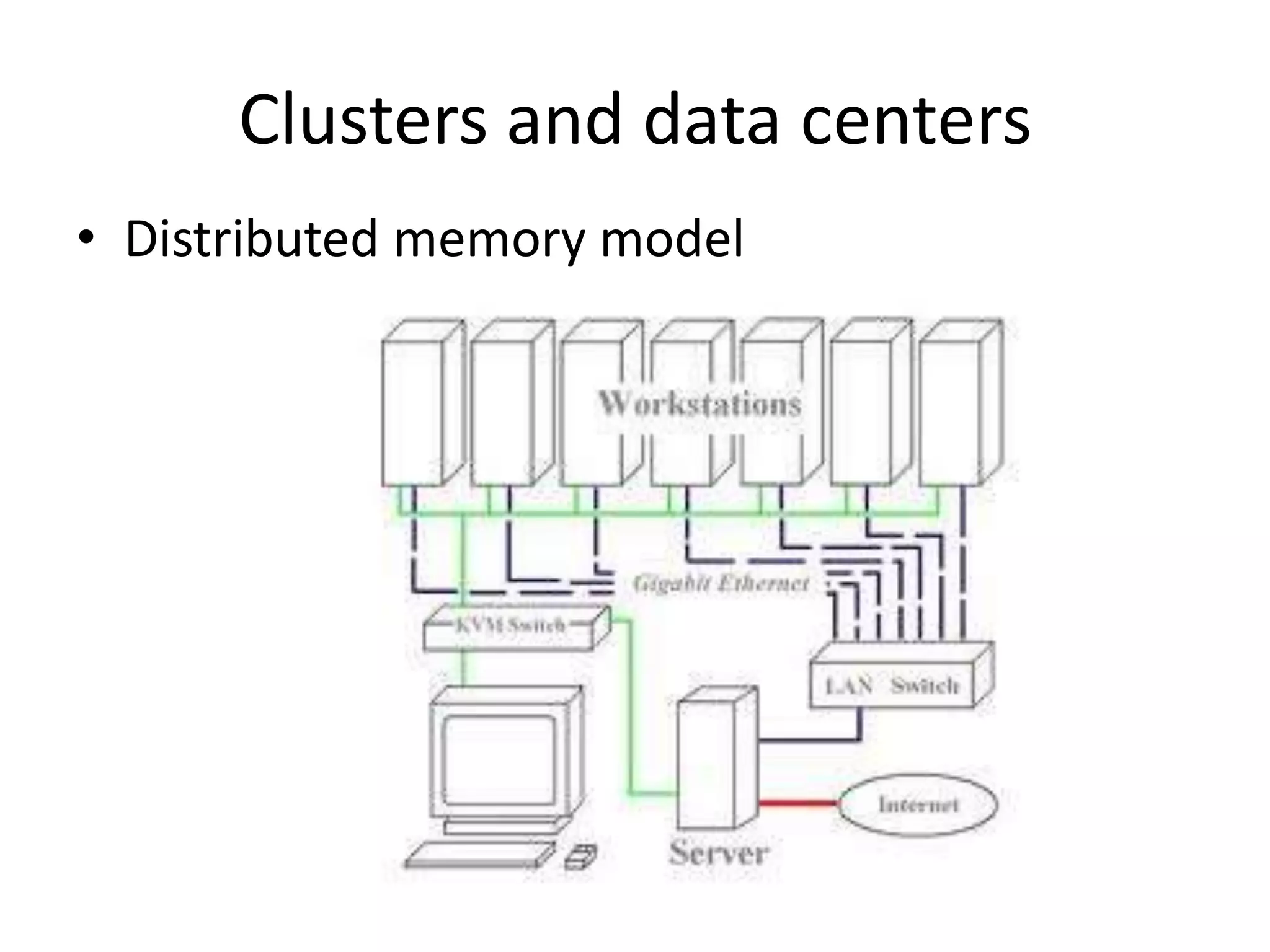
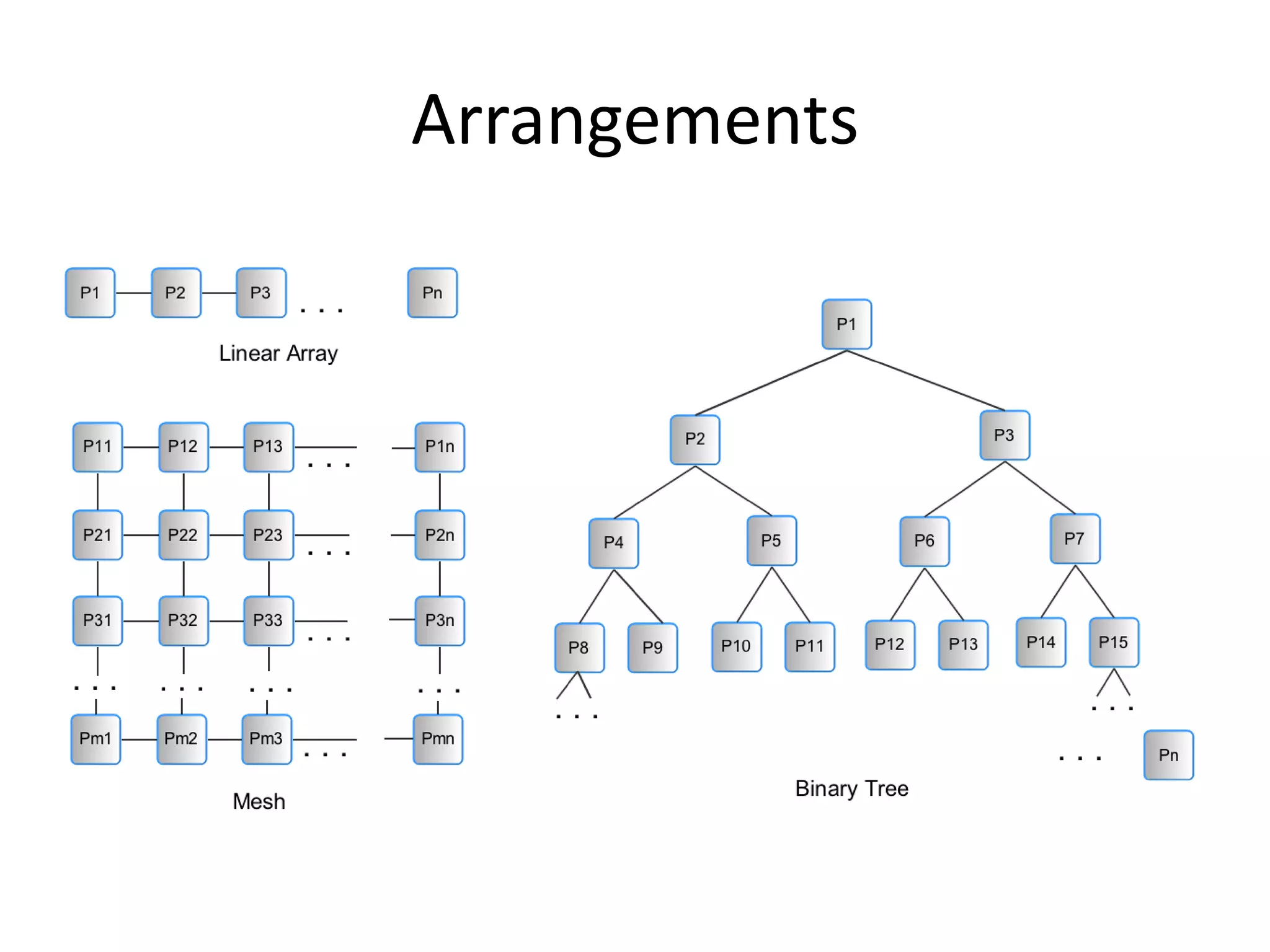
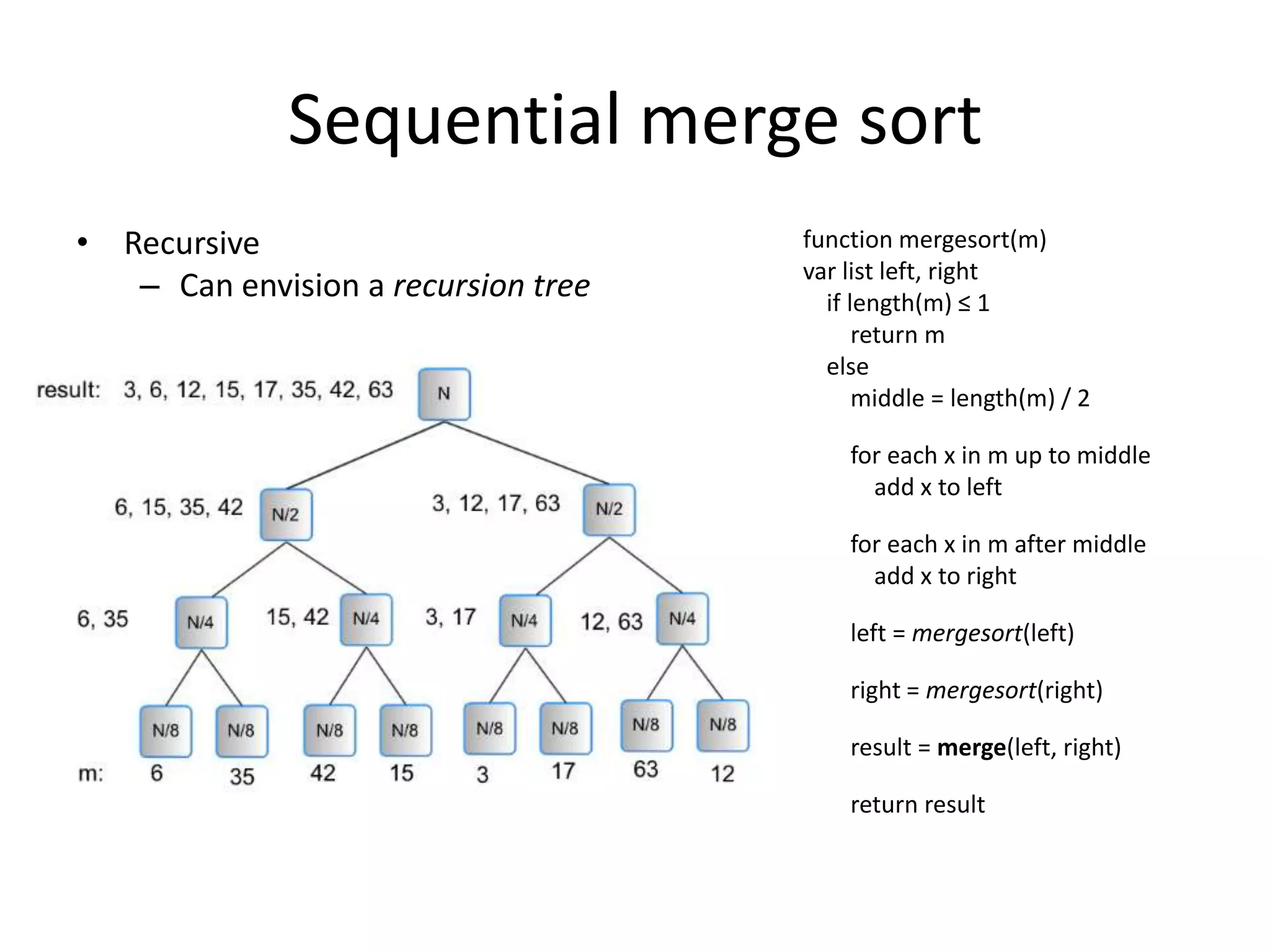
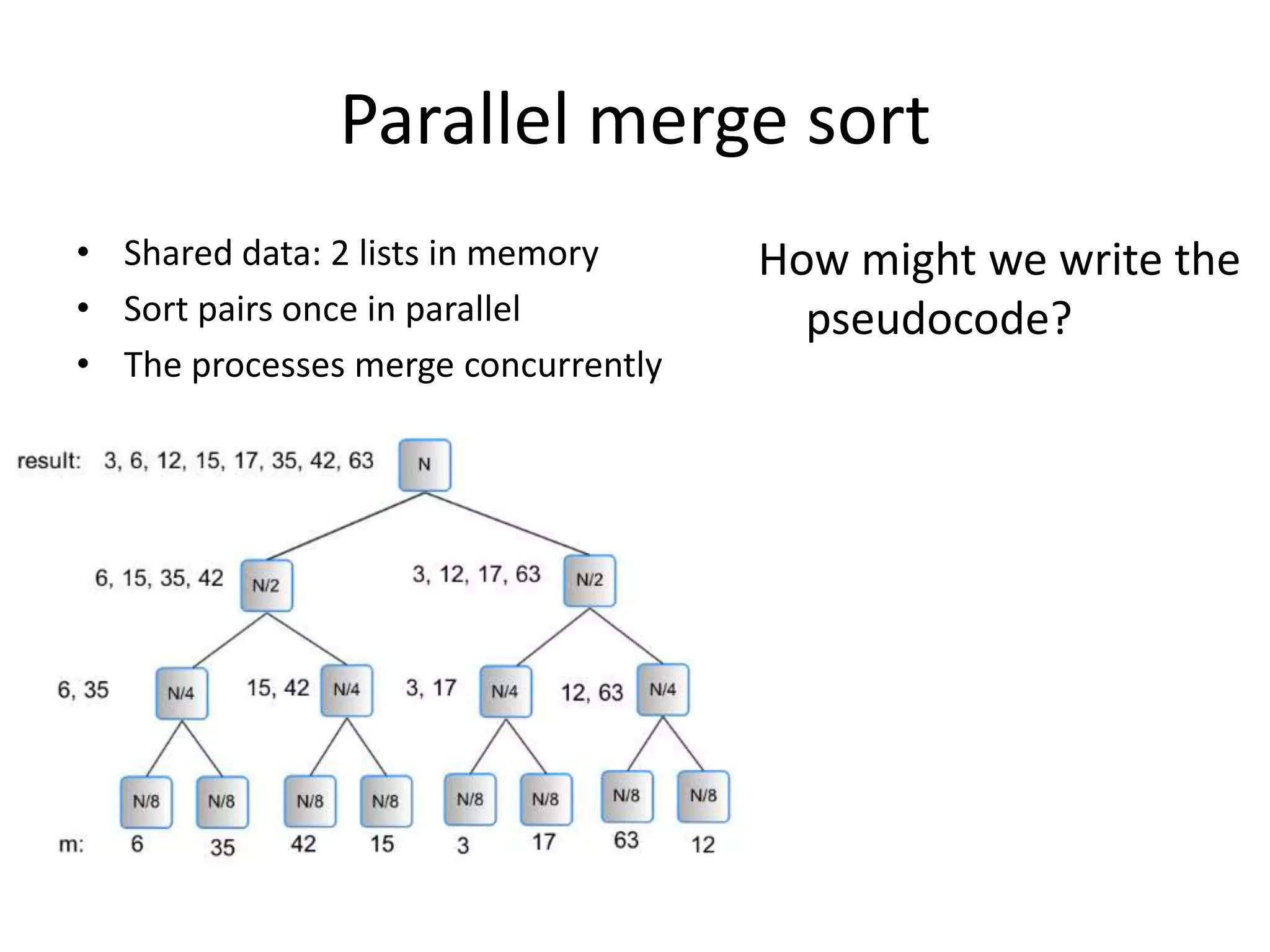
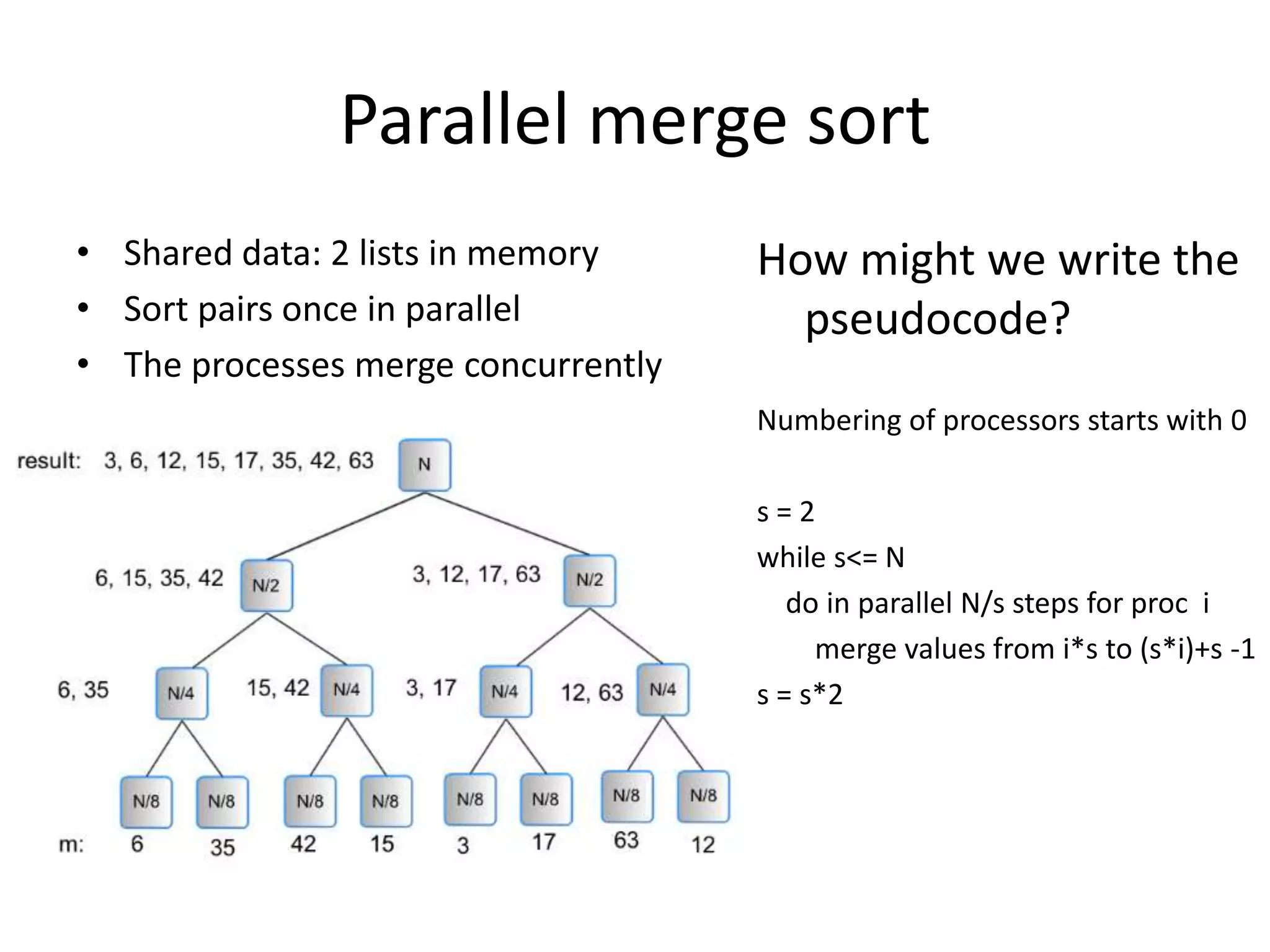
The document discusses parallel algorithms and parallel computing. It begins by explaining that as we consider parallel algorithms, we must understand the hardware they will run on. It then provides some history of parallel processing, noting that since 2005 multicore processors have become common. It introduces the PRAM model of parallel computation and discusses how this theoretical model can be useful for designing parallel algorithms even if not reflective of actual hardware. It provides examples of designing parallel sorting and summing algorithms based on this model.

1. Parallel Algorithms
Sorting
and more

2. Keep hardware in mind
• When considering ‘parallel’ algorithms,
– We have to have an understanding of the
hardware they will run on
– Sequential algorithms: we are doing this implicitly

3. Creative use of processing power
• Lots of data = need for speed
• ~20 years : parallel processing
– Studying how to use multiple processors together
– Really large and complex computations
– Parallel processing was an active sub-field of CS
• Since 2005: the era of multicore is here
– All computers will have >1 processing unit

4. Traditional Computing Machine
• Von Neumann model:
– The stored program computer
• What is this?
– Abstractly, what does it look like?

5. New twist: multiple control units
• It’s difficult to make the CPU any faster
– To increase potential speed, add more CPUs
– These CPUs are called cores
• Abstractly, what might this look like in these
new machines?

6. Shared memory model
• Multiple processors can access memory
locations
• May not scale over time
– As we increase the ‘cores’

7. Other ‘parallel’ configurations:
• Clusters of computers
– Network connects them

8. Other ‘parallel’ configurations
• Massive data centers

9. Clusters and data centers
• Distributed memory model

10. Algorithms
• We will use term processor for the processing
unit that executes instructions
• When considering how to design algorithms for
these architectures
– Useful to start with a base theoretical model
– Revise when implementing on different hardware with
software packages
• Parallel computing course
– Also consider:
• Memory location access by ‘competing’/’cooperating’
processors
• Theoretical arrangement of the processors

11. PRAM model
• Parallel Random Access Machine
• Theoretical
• Abstractly, what does it look like?
• How do processors access memory in this
PRAM model?

12. PRAM model
• Why is using the PRAM model useful when
studying algorithms?

13. PRAM model
• Processors working in parallel
– Each trying to access memory values
– Memory value: what do we mean by this?
• When designing algorithms, we need to
consider what type of memory access that
algorithm requires
• How might our theoretical computer work when many
reads and writes are happening at the same time?

14. Designing algorithms
• With many algorithms, we’re moving data around
– Sort, e.g. Others?
• Concurrent reads by multiple processors
– Memory not changed, so no ‘conflicts’
• Exclusive writes (EW)
– Design pseudocode so that any processor is
exclusively writing a data value into a memory
location

15. Designing Algorithms
• Arranging the processors
– Helpful for design of algorithm
• We can envision how it works
• We can envision the data access pattern needed
– EREW, CREW (CRCW)
– Not how processors are necessarily arranged in
practice
• Although some machines have been
– What are some possible arrangements?
– Why might these arrangements prove useful for
design?

16. Arrangements

17. Sorting in Parallel
Emphasis: merge sort

18. Sequential merge sort
• Recursive function mergesort(m)
var list left, right
– Can envision a recursion tree if length(m) ≤ 1
return m
else
middle = length(m) / 2
for each x in m up to middle
add x to left
for each x in m after middle
add x to right
left = mergesort(left)
right = mergesort(right)
result = merge(left, right)
return result

19. Parallel merge sort
• Shared data: 2 lists in memory How might we write the
• Sort pairs once in parallel pseudocode?
• The processes merge concurrently

20. Parallel merge sort
• Shared data: 2 lists in memory How might we write the
• Sort pairs once in parallel pseudocode?
• The processes merge concurrently
Numbering of processors starts with 0
s=2
while s<= N
do in parallel N/s steps for proc i
merge values from i*s to (s*i)+s -1
s = s*2

21. Parallel Merge Sort
• Work through pseudocode with larger N
• Processor Arrangement: binary tree
• Memory access: EREW
• What was the more practical implementation?

22. Let’s try others
Different from sorting

23. Activity: Sum N integers
• Suppose we have an array of N integers in
memory
• We wish to sum them
– Variant: create a running sum in a new array
• Devise a parallel algorithm for this
– Assume PRAM to start
– What processor arrangement did you use?
– What memory access is required?

24. Next Activity
• Now suppose you need an algorithm for
multiplying a matrix by a vector
X =
Matrix A Vector X Result Vector
Devise a parallel algorithm for this
Assume PRAM to start
Think about what each process will compute- there are options
What processor arrangement did you use?
What memory access is required?

25. Matrix-Vector Multiplication
• The matrix is assumed to be M x N. In other words:
– The matrix has M rows.
– The matrix has N columns.
– For example, a 3 x 2 matrix has 3 rows and 2 columns.
• In matrix-vector multiplication, if the matrix is M x N, then the
vector must have a dimension,N.
– In other words, the vector will have N entries.
– If the matrix is 3 x 2, then the vector must be 3 dimensional.
– This is usually stated as saying the matrix and vector must be
conformable.
• Then, if the matrix and vector are conformable, the
product of the matrix and the vector is a resultant vector
that has a dimension of M.
(So, the result could be a different size than the
original vector!)
For example, if the matrix is 3 x 2, and the vector is 3
dimensional, the result of the multiplication would be
a vector of 2 dimensions

26. Matrix-Vector Multiplication
• Ways to do a parallel algorithm:
– One row of matrix per processor
– One element of matrix per processor
• There is additional overhead involved why?
• What if number of rows M is larger than
number of processors?
• Emerging theme: how to partition the data

27. Expand on previous example
• Matrix – Matrix multiplication
=
X
= ?