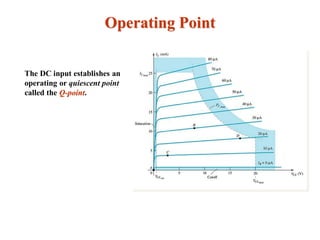
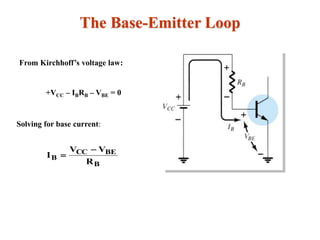
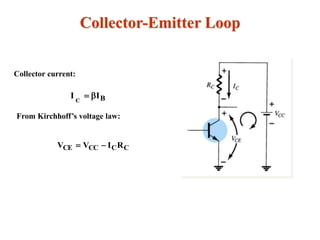
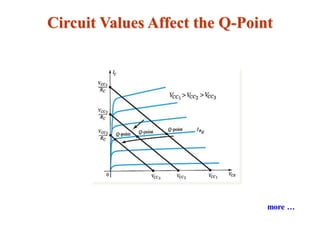
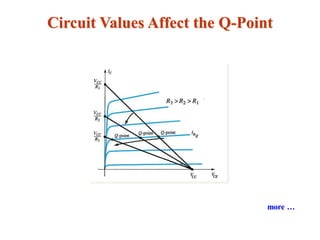
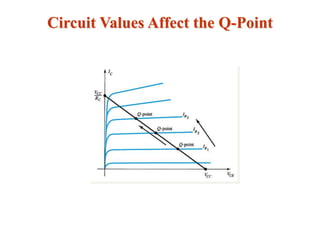
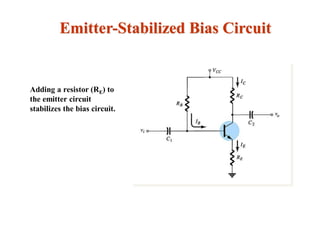
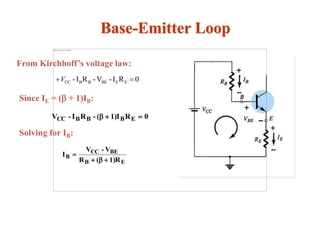
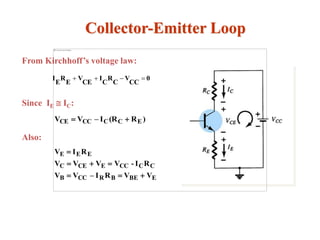
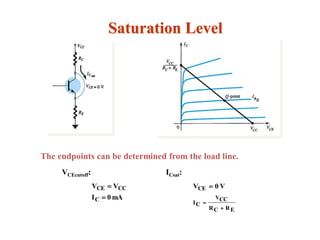
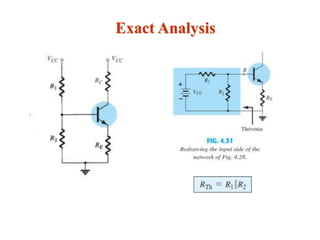
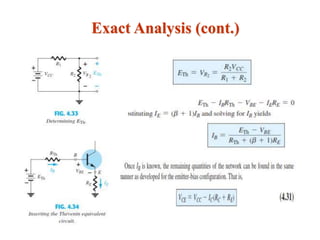
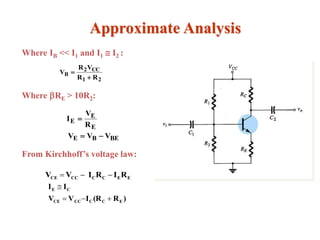
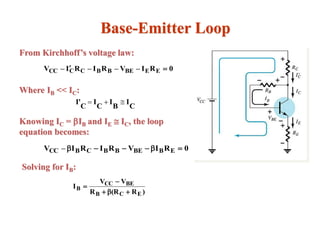
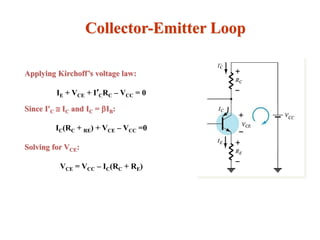
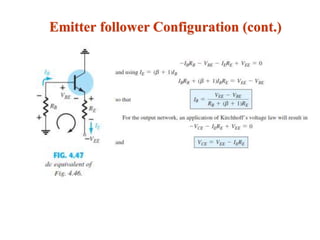
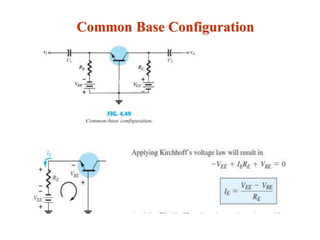
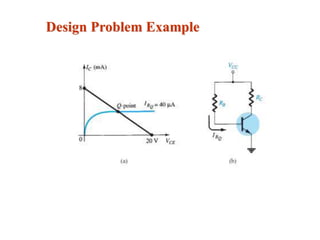
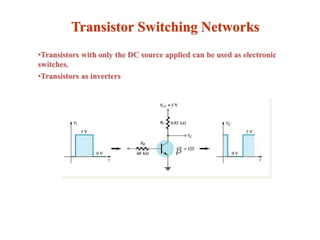
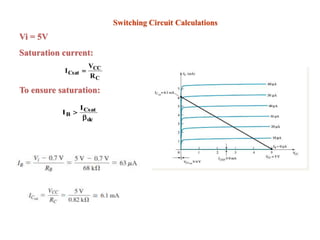
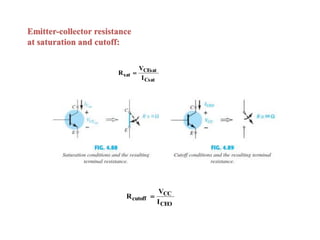
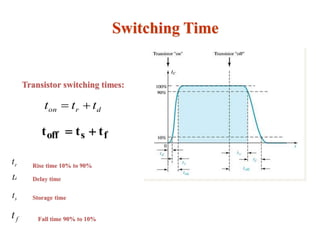
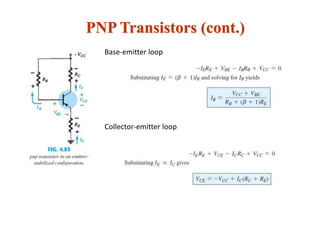
The document explains DC biasing techniques for bipolar junction transistors (BJTs) crucial for establishing operating points in various states (active, cutoff, saturation). It details different biasing circuits, such as fixed-bias, voltage divider bias, and emitter-stabilized bias, emphasizing stability and feedback mechanisms to enhance performance. Additionally, it covers analysis of transistor saturation and troubleshooting methods for biasing circuits.

1. DC Biasing BJT

2. Biasing
Biasing: The DC voltages applied to a transistor in order to turn it on so
that it can amplify the AC signal.

3. Operating Point
The DC input establishes an
operating or quiescent point
called the Q-point.

4. The Three States of Operation
• Active or Linear Region Operation
Base–Emitter junction is forward biased
Base–Collector junction is reverse biased
• Cutoff Region Operation
Base–Emitter junction is reverse biased
• Saturation Region Operation
Base–Emitter junction is forward biased
Base–Collector junction is forward biased

5. DC Biasing Circuits
• Fixed-bias circuit
• Emitter-stabilized bias circuit
• Voltage divider bias circuit
• DC bias with voltage feedback
• Emitter Follower configuration
• Common base configuration

6. Fixed Bias

7. The Base-Emitter Loop
From Kirchhoff’s voltage law:
Solving for base current:
+VCC – IBRB – VBE = 0
B
BECC
B
R
VV
I



8. Collector-Emitter Loop
Collector current:
From Kirchhoff’s voltage law:
BII C

CCCCCE RIVV 

9. Transistor Saturation
When the transistor is operating in saturation, current through the transistor
is at its maximum possible value.
CR
CCV
CsatI 
V0CEV 

10. Load Line Analysis
ICsat
IC = VCC / RC
VCE = 0 V
VCEcutoff
VCE = VCC
IC = 0 mA
• where the value of RB sets the value of
IB
• that sets the values of VCE and IC
The Q-point is the operating point:
The end points of the load line are:

11. Circuit Values Affect the Q-Point
more …

12. Circuit Values Affect the Q-Point
more …

13. Circuit Values Affect the Q-Point

14. Emitter-Stabilized Bias Circuit
Adding a resistor (RE) to
the emitter circuit
stabilizes the bias circuit.

15. Base-Emitter Loop
From Kirchhoff’s voltage law:
0R1)I(-RI-V EBBBCC 
0RI-V-RI- EEBEBBCC V
EB
BECC
B
1)R(R
V-V
I


Since IE = ( + 1)IB:
Solving for IB:

16. Collector-Emitter Loop
From Kirchhoff’s voltage law:
0
CC
V
C
R
C
I
CE
V
E
R
E
I 
Since IE  IC:
)R(RI–VV ECCCCCE 
Also:
EBEBRCCB
CCCCECEC
EEE
VVRI–VV
RI-VVVV
RIV




17. Improved Biased Stability
Stability refers to a circuit condition in which the currents and voltages
will remain fairly constant over a wide range of temperatures and
transistor Beta () values.
Adding RE to the emitter improves the stability of a transistor.

18. Saturation Level
VCEcutoff: ICsat:
The endpoints can be determined from the load line.
mA0I
VV
C
CCCE


ERCR
CCV
CI
CE V0V




19. Voltage Divider Bias
This is a very stable bias
circuit.
The currents and voltages
are nearly independent of
any variations in .

20. Exact Analysis

21. Exact Analysis (cont.)

22. Approximate Analysis
Where IB << I1 and I1  I2 :
Where RE > 10R2:
From Kirchhoff’s voltage law:
21
CC2
B
RR
VR
V


E
E
E
R
V
I 
BEBE VVV 
EECCCCCE RIRIVV 
)R(RIVV
II
ECCCCCE
CE



23. Voltage Divider Bias Analysis
Transistor Saturation Level
EC
CC
CmaxCsat
RR
V
II


Load Line Analysis
Cutoff: Saturation:
mA0I
VV
C
CCCE


V0VCE
ERCR
CCV
CI




24. DC Bias with Voltage Feedback/ Collector
Feedback Configuration
Another way to
improve the stability
of a bias circuit is to
add a feedback path
from collector to
base.
In this bias circuit
the Q-point is only
slightly dependent on
the transistor beta, .

25. Base-Emitter Loop
)R(RR
VV
I
ECB
BECC
B



From Kirchhoff’s voltage law:
0RI–V–RI–RI–V EEBEBBCCCC 
Where IB << IC:
C
I
B
I
C
I
C
I' 
Knowing IC = IB and IE  IC, the loop
equation becomes:
0RIVRIRI–V EBBEBBCBCC 
Solving for IB:

26. Collector-Emitter Loop
Applying Kirchoff’s voltage law:
IE + VCE + I’CRC – VCC = 0
Since IC  IC and IC = IB:
IC(RC + RE) + VCE – VCC =0
Solving for VCE:
VCE = VCC – IC(RC + RE)

27. Saturation Analysis
Transistor Saturation Level
EC
CC
CmaxCsat
RR
V
II


Load Line Analysis
Cutoff: Saturation:
mA0I
VV
C
CCCE


V0VCE
E
R
C
R
CC
V
C
I




28. Emitter follower Configuration
Voltage is taken off from collector
Saturation:

29. Emitter follower Configuration (cont.)

30. Common Base Configuration

31. Common Base Configuration (cont.)

32. Design Problem Example

33. Design Problem: Solution

34. Transistor Switching Networks
•Transistors with only the DC source applied can be used as electronic
switches.
•Transistors as inverters

35. Switching Circuit Calculations
C
CC
Csat
R
V
I 
dc
Csat
B
I
I


Vi = 5V
Saturation current:
To ensure saturation:

36. Vi= 0

37. Emitter-collector resistance
at saturation and cutoff:
Csat
CEsat
sat
I
V
R 
CEO
CC
cutoff
I
V
R 

38. Switching Time
Transistor switching times:
dron ttt 
fsoff ttt 
Rise time 10% to 90%rt
dt
ft
st
Delay time
Storage time
Fall time 90% to 10%

39. PNP Transistors
The analysis for pnp transistor biasing circuits is the same
as that for npn transistor circuits. The only difference is that
the currents are flowing in the opposite direction.

40. PNP Transistors (cont.)
Base-emitter loop
Collector-emitter loop

41. Troubleshooting Hints
• Approximate voltages
– VBE  .7 V for silicon transistors
– VCE  25% to 75% of VCC
• Test for opens and shorts with an ohmmeter.
• Test the solder joints.
• Test the transistor with a transistor tester or a curve tracer.
• Note that the load or the next stage affects the transistor operation.