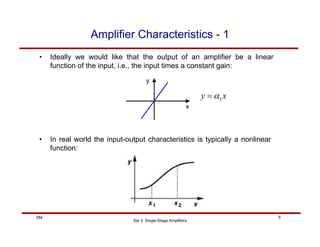
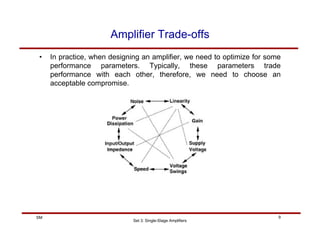
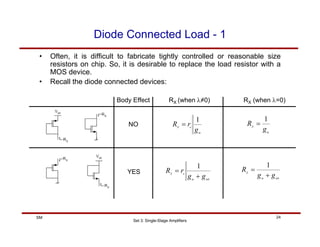
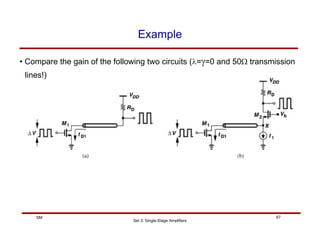
The document discusses single-stage amplifiers, specifically common source amplifiers. It covers the basics of common source amplifiers and different types of loads that can be used, including resistive loads. It analyzes the gain of common source amplifiers with resistive loads using both small-signal and large-signal models, taking into account effects such as channel length modulation. The analysis shows tradeoffs between gain, bandwidth, and voltage swing that must be considered in amplifier design.

1. Set 3: Single-Stage Amplifiers
1
SM
EECE488: Analog CMOS Integrated Circuit Design
3. Single-Stage Amplifiers
Shahriar Mirabbasi
Department of Electrical and Computer Engineering
University of British Columbia
shahriar@ece.ubc.ca
Technical contributions of Pedram Lajevardi in revising the course notes are greatly acknowledged.

2. Set 3: Single-Stage Amplifiers
2
SM
Overview
1. Why Amplifiers?
2. Amplifier Characteristics
3. Amplifier Trade-offs
4. Single-stage Amplifiers
5. Common Source Amplifiers
1. Resistive Load
2. Diode-connected Load
3. Current Source Load
4. Triode Load
5. Source Degeneration

3. Set 3: Single-Stage Amplifiers
3
SM
Overview
6. Common-Drain (Source-Follower) Amplifiers
1. Resistive Load
2. Current Source Load
3. Voltage Division in Source Followers
7. Common-Gate Amplifiers
6. Cascode Amplifiers

4. Set 3: Single-Stage Amplifiers
4
SM
Reading Assignments
• Reading:
Chapter 3 of Razavi’s book
• In this set of slides we will study low-frequency small-signal behavior of
single-stage CMOS amplifiers. Although, we assume long-channel
MOS models (not a good assumption for deep submicron technologies)
the techniques discussed here help us to develop basic circuit intuition
and to better understand and predict the behavior of circuits.
Most of the figures in these lecture notes are © Design of Analog
CMOS Integrated Circuits, McGraw-Hill, 2001.

5. Set 3: Single-Stage Amplifiers
5
SM
Why Amplifiers?
• Amplifiers are essential building blocks of both analog and digital
systems.
• Amplifiers are needed for variety of reasons including:
– To amplify a weak analog signal for further processing
– To reduce the effects of noise of the next stage
– To provide a proper logical levels (in digital circuits)
• Amplifiers also play a crucial role in feedback systems
• We first look at the low-frequency performance of amplifiers. Therefore,
all capacitors in the small-signal model are ignored!

6. Set 3: Single-Stage Amplifiers
6
SM
Amplifier Characteristics - 1
• Ideally we would like that the output of an amplifier be a linear
function of the input, i.e., the input times a constant gain:
x
y 1
α
=
x
y
• In real world the input-output characteristics is typically a nonlinear
function:

7. Set 3: Single-Stage Amplifiers
7
SM
Amplifier Characteristics - 2
• It is more convenient to use a linear approximation of a nonlinear
function.
• Use the tangent line to the curve at the given (operating) point.
x
y
• The larger the signal changes about the operating point, the worse the
approximation of the curve by its tangent line.
• This is why small-signal analysis is so popular!

8. Set 3: Single-Stage Amplifiers
8
SM
Amplifier Characteristics - 3
• Let to get:
n
n x
x
x
x
x
x
y )
(
)
(
)
( 0
2
0
2
0
1
0 −
+
+
−
+
−
+
≈ α
α
α
α L
)
( 0
1
0 x
x
y −
+
≈ α
α
x
y
x
f
y
y ∆
≈
−
=
−
=
∆ 1
0
0 )
( α
α
• If x-x0=∆x is small, we can ignore the higher-order terms (hence the
name small-signal analysis) to get:
• α0 is referred to as the operating (bias) point and α1 is the small-signal
gain.
!
)
( 0
n
x
f n
n =
α
• A well-behaved nonlinear function in the vicinity of a given point can be
approximated by its corresponding Taylor series:
n
n
x
x
n
x
f
x
x
x
f
x
x
x
f
x
f
y )
(
!
)
(
)
(
!
2
)
(
'
'
)
(
)
(
'
)
( 0
0
2
0
0
0
0
0 −
⋅
+
+
−
⋅
+
−
⋅
+
≈ L

9. Set 3: Single-Stage Amplifiers
9
SM
• In practice, when designing an amplifier, we need to optimize for some
performance parameters. Typically, these parameters trade
performance with each other, therefore, we need to choose an
acceptable compromise.
Amplifier Trade-offs

10. Set 3: Single-Stage Amplifiers
10
SM
Single-Stage Amplifiers
• We will examine the following types of amplifiers:
1. Common Source
2. Common Drain (Source Follower )
3. Common Gate
4. Cascode and Folded Cascode
• Each of these amplifiers have some advantages and some
disadvantages. Often, designers have to utilize a cascade combination
of these amplifiers to meet the design requirements.

11. Set 3: Single-Stage Amplifiers
11
SM
Common Source Basics - 1
• In common-source amplifiers, the input is (somehow!) connected to the
gate and the output is (somehow!) taken from the drain.
• We can divide common source amplifiers into two groups:
1. Without source degeneration (no body
effect for the main transistor):
2. With source degeneration (have to take
body effect into account for the main
transistor):

12. Set 3: Single-Stage Amplifiers
12
SM
Common Source Basics - 2
In a simple common source amplifier:
• gate voltage variations times gm gives the drain current
variations,
• drain current variations times the load gives the output voltage
variations.
• Therefore, one can expect the small-signal gain to be:
D
m
v R
g
A ⋅
=

13. Set 3: Single-Stage Amplifiers
13
SM
Common Source Basics - 3
• Different types of loads can be used in an amplifier:
1. Resistive Load
2. Diode-connected Load
3. Current Source Load
4. Triode Load
• The following parameters of amplifiers are very important:
1. Small-signal gain
2. Voltage swing

14. Set 3: Single-Stage Amplifiers
14
SM
Resistive Load - 1
• Let’s use a resistor as the load.
• The region of operation of M1 depends on its size and the values of Vin
and R.
• We are interested in the small-signal gain and the headroom (which
determines the maximum voltage swing).
• We will calculate the gain using two different methods
1. Small-signal model
2. Large-signal analysis

15. Set 3: Single-Stage Amplifiers
15
SM
Resistive Load - 2
Gain – Method 1: Small-Signal Model
• This is assuming that the transistor is in saturation, and channel length
modulation is ignored.
• The current through RD:
• Output Voltage:
• Small-signal Gain:
IN
m
D
v
g
i ⋅
=
D
IN
m
D
D
OUT
R
v
g
R
i
v ⋅
⋅
−
=
⋅
−
=
D
m
IN
OUT
v
R
g
v
v
A ⋅
−
=
=

16. Set 3: Single-Stage Amplifiers
16
SM
Resistive Load - 3
Gain – Method 2: Large-Signal Analysis
• If VIN<VTH, M1 is off, and VOUT= VDD = VDS.
m
D
TH
IN
ox
n
D
IN
OUT
v
TH
IN
ox
n
D
dd
D
D
dd
OUT
g
R
V
V
L
W
C
R
V
V
A
V
V
L
W
C
R
V
i
R
V
V
⋅
−
=
−
⋅
⋅
⋅
⋅
−
=
∂
∂
=
−
⋅
⋅
⋅
⋅
⋅
−
=
⋅
−
=
)
(
)
(
2
1 2
µ
µ
• As VIN becomes slightly larger than VTH, M1 turns on and goes into
saturation (VDS≈ VDD > VGS- VTH ≈0).
0
=
∂
∂
=
=
⋅
−
=
IN
OUT
v
DD
D
D
DD
OUT
V
V
A
V
i
R
V
V
• As VIN increases, VDS decreases, and M1 goes into triode when
VIN- VTH = VOUT. We can find the value of VIN that makes M1 switch
its region of operation.
)
(
)
(
2
1 2
TH
IN
TH
IN
ox
n
D
dd
D
D
dd
OUT
V
V
V
V
L
W
C
R
V
i
R
V
V −
=
−
⋅
⋅
⋅
⋅
⋅
−
=
⋅
−
= µ

17. Set 3: Single-Stage Amplifiers
17
SM
Resistive Load - 4
Gain – Method 2: Large-Signal Analysis (Continued)
• As VIN increases, VDS decreases, and M1 goes into triode.
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
∂
∂
⋅
−
+
∂
∂
⋅
−
⋅
⋅
⋅
⋅
−
=
∂
∂
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
⋅
−
⋅
⋅
⋅
⋅
−
=
⋅
−
=
IN
OUT
OUT
OUT
IN
OUT
TH
IN
ox
n
D
IN
OUT
OUT
OUT
TH
IN
ox
n
D
DD
D
D
DD
OUT
V
V
V
V
V
V
V
V
L
W
C
R
V
V
V
V
V
V
L
W
C
R
V
i
R
V
V
)
(
2
)
(
2
µ
µ
• We can find Av from above. It will depend on both VIN and VOUT.
• If VIN increases further, M1 goes into deep triode if VOUT<< 2(VIN- VTH).
D
ON
ON
DD
ON
D
DD
TH
IN
ox
n
D
DD
OUT
OUT
TH
IN
ox
n
D
DD
D
D
DD
OUT
R
R
R
V
R
R
V
V
V
L
W
C
R
V
V
V
V
V
L
W
C
R
V
i
R
V
V
+
⋅
=
⋅
+
=
−
⋅
⋅
⋅
⋅
+
=
⋅
−
⋅
⋅
⋅
⋅
−
=
⋅
−
=
1
1
)
(
1
)
(
µ
µ

18. Set 3: Single-Stage Amplifiers
18
SM
Resistive Load - 5
Example: Sketch the drain current and gm of M1 as a function of VIN.
• gm depends on VIN, so if VIN changes by a large amount the small-
signal approximation will not be valid anymore.
• In order to have a linear amplifier, we don’t want gain to depend on
parameters like gm which depend on the input signal.

19. Set 3: Single-Stage Amplifiers
19
SM
Resistive Load - 6
• Gain of common-source amplifier:
• To increase the gain:
1. Increase gm by increasing W or VIN (DC portion or bias). Either way,
ID increases (more power) and VRD increases, which limits the
voltage swing.
2. Increase RD and keep ID constant (gm and power remain constant).
But, VRD increases which limits the voltage swing.
3. Increase RD and reduce ID so VRD remains constant.
¾ If ID is reduced by decreasing W, the gain will not change.
¾ If ID is reduced by decreasing VIN (bias), the gain will increase.
Since RD is increased, the bandwidth becomes smaller (why?).
• Notice the trade-offs between gain, bandwidth, and voltage swings.
eff
RD
D
RD
ox
n
D
RD
TH
IN
ox
n
D
m
v
V
V
I
V
L
W
C
I
V
V
V
L
W
C
R
g
A
⋅
−
=
⋅
−
=
⋅
−
−
=
⋅
−
=
2
2
)
( µ
µ

20. Set 3: Single-Stage Amplifiers
20
SM
Resistive Load - 7
• Now let’s consider the simple common-source circuit with channel
length modulation taken into account.
• Channel length modulation becomes more important as RD increases
(in the next slide we will see why!).
• Again, we will calculate the gain in two different methods
1. Small-signal Model
2. Large Signal Analysis

21. Set 3: Single-Stage Amplifiers
21
SM
Resistive Load - 8
Gain – Method 1: Small-Signal Model
• This is assuming that the transistor is in saturation.
• The current through RD:
• Output Voltage:
• Small-signal Gain:
IN
m
D
v
g
i ⋅
=
( ) ( )
o
D
IN
m
o
D
D
OUT
r
R
v
g
r
R
i
v ⋅
⋅
−
=
⋅
−
=
( )
o
D
m
IN
OUT
v
r
R
g
v
v
A ⋅
−
=
=

22. Set 3: Single-Stage Amplifiers
22
SM
Resistive Load - 9
Gain – Method 2: Large-Signal Analysis
( )
( )
( )
( )
o
D
m
D
o
m
D
o
o
D
m
D
D
D
m
D
TH
IN
ox
n
D
OUT
TH
IN
ox
n
D
v
IN
OUT
TH
IN
OUT
TH
IN
ox
n
D
IN
OUT
OUT
TH
IN
ox
n
D
DD
D
D
DD
OUT
r
R
g
R
r
g
R
r
r
R
g
R
I
R
g
R
V
V
L
W
C
R
V
V
V
L
W
C
R
A
V
V
V
V
V
V
V
L
W
C
R
V
V
V
V
V
L
W
C
R
V
I
R
V
V
⋅
−
=
+
⋅
⋅
−
=
⋅
+
⋅
−
=
λ
⋅
⋅
+
⋅
−
=
λ
⋅
−
⋅
⋅
⋅
µ
⋅
⋅
+
⋅
λ
+
⋅
−
⋅
⋅
⋅
µ
⋅
−
=
⎥
⎦
⎤
⎢
⎣
⎡
∂
∂
⋅
λ
⋅
−
⋅
+
⋅
λ
+
⋅
−
⋅
⋅
⋅
µ
⋅
−
=
∂
∂
⋅
λ
+
⋅
−
⋅
⋅
⋅
µ
⋅
⋅
−
=
⋅
−
=
1
1
1
)
(
2
1
1
1
)
(
)
(
2
1
1
)
(
1
)
(
2
1
2
2
• As VIN becomes slightly larger than VTH, M1 turns on and goes into
saturation (VDS≈ VDD > VGS- VTH ≈0).

23. Set 3: Single-Stage Amplifiers
23
SM
Resistive Load - 10
Example:
• Assuming M1 is biased in active region, what is the
small-signal gain of the following circuit?
( ) o
m
o
m
IN
OUT
v
r
g
r
g
v
v
A ⋅
−
=
∞
⋅
−
=
=
• I1 is a current source and ideally has an infinite impedance.
• This is the maximum gain of this amplifier (why?), and is known as the
intrinsic gain.
• How can VIN change if I1 is constant?
( )
OUT
TH
IN
ox
n
D
V
V
V
L
W
C
I ⋅
+
⋅
−
⋅
⋅
⋅
⋅
= λ
µ 1
)
(
2
1 2
• Here we have to take channel-length modulation into account. As VIN
changes, VOUT also changes to keep I1 constant.

24. Set 3: Single-Stage Amplifiers
24
SM
Diode Connected Load - 1
• Often, it is difficult to fabricate tightly controlled or reasonable size
resistors on chip. So, it is desirable to replace the load resistor with a
MOS device.
• Recall the diode connected devices:
Body Effect RX (when λ≠0) RX (when λ=0)
NO
YES
m
o
X
g
r
R
1
=
m
X
g
R
1
=
mb
m
o
X
g
g
r
R
+
=
1
mb
m
X
g
g
R
+
=
1

25. Set 3: Single-Stage Amplifiers
25
SM
Diode Connected Load - 2
• Now consider the common-source amplifier with two types of diode
connected loads:
1. PMOS diode connected load:
(No body effect)
2. NMOS diode connected load:
(Body effect has to be taken into account)

26. Set 3: Single-Stage Amplifiers
26
SM
Diode Connected Load - 3
PMOS Diode Connected Load:
• Note that this is a common source configuration
with M2 being the load. We have:
( ) ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
−
=
⋅
−
=
= 1
2
2
1
1
1
1
o
o
m
m
o
X
m
IN
OUT
v
r
r
g
g
r
R
g
v
v
A
• Ignoring the channel length modulation (ro1=ro2=∞), we can write:
1
1
2
2
2
2
2
1
1
1
2
1
2
1
2
2
1
1
2
1
2
1
2
2
2
2
1
TH
GS
TH
SG
TH
SG
D
TH
GS
D
m
m
v
p
n
D
ox
p
D
ox
n
m
m
m
m
v
V
V
V
V
V
V
I
V
V
I
g
g
A
L
W
L
W
I
L
W
C
I
L
W
C
g
g
g
g
A
−
−
−
=
−
⋅
−
⋅
−
=
−
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
µ
⎟
⎠
⎞
⎜
⎝
⎛
⋅
µ
−
=
⋅
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅
µ
⋅
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅
µ
−
=
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∞
∞
⋅
−
=

27. Set 3: Single-Stage Amplifiers
27
SM
Diode Connected Load - 4
NMOS Diode Connected Load:
• Again, note that this is a common source configuration
with M2 being the load. We have:
( ) ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
⋅
−
=
⋅
−
=
= 1
2
2
2
1
1
1
1
o
o
mb
m
m
o
X
m
IN
OUT
v
r
r
g
g
g
r
R
g
v
v
A
• Ignoring the channel length modulation (ro1=ro2=∞), we can write:
TH
GS
TH
GS
v
m
m
mb
m
m
mb
m
m
v
V
V
V
V
L
W
L
W
A
g
g
g
g
g
g
g
g
A
−
−
⋅
+
−
=
⎟
⎠
⎞
⎜
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
+
−
=
+
⋅
−
=
+
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∞
∞
+
⋅
−
=
1
2
2
1
2
1
2
2
1
2
2
1
1
1
1
1
)
1
(
1
η
η
η

28. Set 3: Single-Stage Amplifiers
28
SM
Diode Connected Load - 5
• For a diode connected load we observe that (to the first order
approximation):
1. The amplifier gain is not a function of the bias current. So,
the change in the input and output levels does not affect the
gain, and the amplifier becomes more linear.
2. The amplifier gain is not a function of the input signal
(amplifier becomes more linear).
3. The amplifier gain is a weak function (square root) of the
transistor sizes. So, we have to change the dimensions by a
considerable amount so as to increase the gain.

29. Set 3: Single-Stage Amplifiers
29
SM
Diode Connected Load - 6
4. The gain of the amplifier is reduced when body effect
should be considered.
5. We want M1 to be in saturation, and M2 to be on (M2 cannot
be in triode (why?)):
6. The voltage swing is constrained by both the required
overdrive voltages and the threshold voltage of the diode
connected device.
7. A high amplifier gain leads to a high overdrive voltage for
the diode connected device which limits the voltage swing.
2
1
1
1 :
2
,
:
1 TH
DD
OUT
eff
TH
GS
OUT V
V
V
M
V
V
V
V
M −
<
=
−
>

30. Set 3: Single-Stage Amplifiers
30
SM
Diode Connected Load - 6
Example:
• Find the gain of the following circuit if M1 is biased in saturation and
Is=0.75I1.
( ) ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∞
⋅
−
=
⋅
−
=
= 1
2
2
1
1
2
2
1
1
1
1
1
o
o
m
m
o
o
m
m
o
Is
X
m
IN
OUT
v
r
r
g
g
r
r
g
g
r
r
R
g
v
v
A
• Ignoring the channel length modulation (ro1=ro2=∞) we get:
1
1
2
2
2
1
2
2
2
1
1
1
2
2
1
1
2
1
2
1
4
2
2
2
2
2
1
TH
GS
TH
SG
p
n
v
TH
SG
D
TH
GS
D
D
ox
p
D
ox
n
m
m
m
m
v
V
V
V
V
L
W
L
W
A
V
V
I
V
V
I
I
L
W
C
I
L
W
C
g
g
g
g
A
−
−
⋅
−
=
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅
−
=
−
⋅
−
⋅
−
=
⋅
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅
⋅
⎟
⎠
⎞
⎜
⎝
⎛
⋅
⋅
−
=
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∞
∞
⋅
−
=
µ
µ
µ
µ

31. Set 3: Single-Stage Amplifiers
31
SM
Diode Connected Load - 7
Example (Continued):
• We observe for this example that:
1. For fixed transistor sizes, using the current source increases the
gain by a factor of 2.
2. For fixed overdrive voltages, using the current source increases
the gain by a factor of 4.
3. For a given gain, using the current source allows us to make the
diode connected load 4 times smaller.
4. For a given gain, using the current source allows us to make the
overdrive voltage of the diode connected load 4 times smaller.
This increases the headroom for voltage swing.

32. Set 3: Single-Stage Amplifiers
32
SM
Current Source Load - 1
• Note that current source M2 is the load.
•
• Recall that the output impedance of M2 seen from Vout:
( ) ( )
1
2
1
1
1
2
o
o
m
o
X
m
IN
OUT
v
o
X
X
X
r
r
g
r
R
g
v
v
A
r
i
v
R
⋅
−
=
⋅
−
=
=
=
=
• For large gain at given power, we want large ro and
Increase L and W keeping the aspect ratio constant (so ro increases
and ID remains constant). However, this approach increases the
capacitance of the output node.
• We want M2 to be in saturation so
W
L
L
W
L
I
r
D
o
2
1
1
1
=
⋅
∝
⋅
λ
=
2
2
2
2 eff
DD
OUT
eff
TH
SG
OUT
DD
SD V
V
V
V
V
V
V
V
V −
<
→
=
−
>
−
=

33. Set 3: Single-Stage Amplifiers
33
SM
Current Source Load - 2
• We also want M1 to be in saturation:
1
1
1
1 eff
OUT
eff
TH
GS
OUT
DS
V
V
V
V
V
V
V >
→
=
−
>
=
• Thus, we want Veff1 and Veff2 to be small, so that there is more
headroom for output voltage swing. For a constant ID, we can increase
W1 and W2 to reduce Veff1 and Veff2.
• The intrinsic gain of this amplifier is:
• In general, we have:
o
m
v
r
g
A ⋅
−
=
L
A
W
L
r
L
W
g v
o
m
∝
→
∝
∝
2
,
• But since current in this case is roughly constant:
LW
A
L
I
r
L
W
I
L
W
C
g v
D
o
D
ox
n
m
∝
→
∝
⋅
=
∝
⋅
⋅
⋅
=
λ
µ
1
,
2

34. Set 3: Single-Stage Amplifiers
34
SM
Triode Load
• We recognize that this is a common source
configuration with M2 being the load. Recall that if
M2 is in deep triode, i.e., VSD<<2(VSG-|VTH|), it
behaves like a resistor.
( )
( ) ( )
( )
1
2
1
2
,
1
1
:
2
o
ON
m
v
TH
b
dd
ox
p
TH
SG
ox
p
ON
TH
SG
SD
r
R
g
A
V
V
V
L
W
C
V
V
L
W
C
R
V
V
V
If
⋅
−
=
−
−
⋅
⋅
⋅
=
−
⋅
⋅
⋅
=
−
<<
µ
µ
• Vb should be low enough to make sure that M2 is in deep triode region
and usually requires additional complexity to be precisely generated.
• RON2 depends on µp, Cox, and VTH which in turn depend on the
technology being used.
• In general, this amplifier with triode load is difficult to design and use!
• However, compared to diode-connected load, triode load consumes less
headroom:
DD
OUT
eff
TH
GS
OUT V
V
M
V
V
V
V
M ≈
=
−
> :
,
: 2
1
1
1

35. Set 3: Single-Stage Amplifiers
35
SM
Source Degeneration - 1
• The following circuit shows a common source configuration
with a degeneration resistor in the source.
• We will show that this configuration makes the common
source amplifier more linear.
• We will use two methods to derive the gain of this circuit:
1. Small-signal Model
2. Using the following Lemma
Lemma:
In linear systems, the voltage gain is equal to –GmRout.

36. Set 3: Single-Stage Amplifiers
36
SM
Source Degeneration - 2
Gain – Method 1: Small Signal Model
( )
( ) S
D
S
mb
m
O
D
O
m
IN
OUT
v
D
IN
m
O
S
O
D
S
mb
S
m
OUT
O
S
D
OUT
OUT
S
D
OUT
mb
S
D
OUT
IN
m
D
OUT
S
D
OUT
S
OUT
BS
S
D
OUT
IN
S
OUT
IN
D
OUT
OUT
O
S
OUT
OUT
BS
mb
m
OUT
R
R
R
g
g
r
R
r
g
v
v
A
R
v
g
r
R
r
R
R
g
R
g
v
r
R
R
v
v
R
R
v
g
R
R
v
v
g
R
v
R
R
v
R
i
v
R
R
v
v
R
i
v
v
R
v
i
r
R
i
v
v
g
v
g
i
+
+
⋅
+
+
⋅
⋅
⋅
−
=
=
⋅
⋅
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
⋅
+
⋅
+
⋅
⋅
+
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
⋅
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
+
⋅
=
−
⋅
=
⋅
−
=
⋅
+
=
⋅
−
=
−
=
⋅
−
+
⋅
+
⋅
=
1
1
,
,
1
1

37. Set 3: Single-Stage Amplifiers
37
SM
Source Degeneration - 3
Gain – Method 2: Lemma
• The Lemma states that in linear systems, the voltage gain is
equal to –GmRout. So we need to find Gm and Rout.
1. Gm:
Recall that the equivalent transconductance of the above
Circuit is:
( ) ( ) S
S
mb
m
m
S
S
mb
S
m
m
m
R
R
g
g
r
r
g
R
R
g
R
g
r
r
r
g
v
i
G
O
O
O
O
O
IN
OUT
+
⋅
+
+
⋅
=
+
⋅
+
⋅
⋅
+
⋅
=
=
]
1
[

38. Set 3: Single-Stage Amplifiers
38
SM
Source Degeneration - 4
Gain – Method 2: Lemma (Continued)
1. ROUT:
We use the following small signal model to derive the small
signal output impedance of this amplifier:
( )
( ) ( )
( )
( ) ( )
( )
( )
( )
( ) D
O
S
mb
m
S
D
O
S
mb
m
S
D
X
OUT
O
S
mb
m
S
O
S
mb
S
m
S
X
X
X
O
S
X
mb
S
X
m
X
S
X
O
BS
mb
m
X
S
X
X
S
X
BS
S
X
R
r
R
g
g
R
R
r
R
g
g
R
R
R
R
r
R
g
g
R
r
R
g
R
g
R
i
v
R
r
R
i
g
R
i
g
i
R
i
r
v
g
v
g
i
R
i
v
R
i
v
R
i
v
+
⋅
⋅
+
+
+
⋅
⋅
⋅
+
+
+
=
=
⋅
⋅
+
+
+
=
⋅
⋅
+
⋅
+
+
=
=
⋅
⋅
−
⋅
−
⋅
−
⋅
−
+
⋅
=
⋅
⋅
−
⋅
−
+
⋅
=
⋅
−
=
⋅
−
=
)
(
1
)
(
1
)
(
1
1
,
1
1
• Since typically rO>>RS:
( ) ( ) ( ) O
S
mb
m
O
S
mb
m
O
S
mb
m
S
X r
R
g
g
r
R
g
g
r
R
g
g
R
R ⋅
⋅
+
=
⋅
⋅
+
+
=
⋅
⋅
+
+
+
= )
(
1
)
(
1

39. Set 3: Single-Stage Amplifiers
39
SM
Source Degeneration - 5
Gain – Method 2: Lemma (Continued)
( )
( )
( )
( )
( ) D
O
S
mb
m
O
D
O
m
D
S
O
mb
O
m
O
D
S
O
mb
O
m
O
S
S
mb
S
m
O
O
O
m
OUT
m
v
R
r
R
g
g
r
R
r
g
R
R
r
g
r
g
r
R
R
r
g
r
g
r
R
R
g
R
g
r
r
r
g
R
G
A
+
⋅
⋅
+
+
+
⋅
⋅
−
=
+
⋅
⋅
+
⋅
+
+
⋅
⋅
⋅
+
⋅
+
+
⋅
+
⋅
+
⋅
⋅
+
⋅
−
=
⋅
−
=
)
(
1
1
1
( )
( )
( ) D
O
S
mb
m
S
D
O
S
mb
m
S
OUT
R
r
R
g
g
R
R
r
R
g
g
R
R
+
⋅
⋅
+
+
+
⋅
⋅
⋅
+
+
+
=
)
(
1
)
(
1
( ) S
S
mb
m
O
O
m
m
R
R
g
g
r
r
g
G
+
⋅
+
⋅
+
⋅
=
)
1
(

40. Set 3: Single-Stage Amplifiers
40
SM
Source Degeneration - 6
• If we ignore body effect and channel-length modulation:
Method 1 – Small-signal Model:
S
m
D
m
OUT
m
v
R
g
R
g
R
G
A
⋅
+
⋅
−
=
⋅
−
=
1
( )
( )
( )
( )
( )
( ) D
S
mb
m
D
S
mb
m
D
S
O
mb
O
m
O
D
S
O
mb
O
m
O
OUT
R
R
g
g
R
R
g
g
R
R
r
g
r
g
r
R
R
r
g
r
g
r
R
mb
g
o
r
=
⋅
+
+
⋅
⋅
+
+
=
+
⋅
⋅
+
⋅
+
+
⋅
⋅
⋅
+
⋅
+
+
=
→
∞
→
1
1
1
1
lim
0
( ) ( ) S
m
m
S
mb
m
m
S
S
mb
S
m
O
O
O
m
m
R
g
g
R
g
g
g
R
R
g
R
g
r
r
r
g
G
mb
g
o
r
⋅
+
=
⋅
+
+
=
+
⋅
+
⋅
⋅
+
⋅
=
→
∞
→
1
1
lim
0
S
m
D
m
IN
OUT
v
S
m
IN
GS
S
GS
m
IN
GS
D
GS
m
OUT
R
g
R
g
v
v
A
R
g
v
v
R
v
g
v
v
R
v
g
v
⋅
+
⋅
−
=
=
→
⋅
+
⋅
=
⋅
⋅
−
=
⋅
⋅
−
=
1
1
1
,
Method 2 – Taking limits:

41. Set 3: Single-Stage Amplifiers
41
SM
Source Degeneration - 7
Obtaining Gm and Rout directly assuming λ=γ=0:
1. Gm:
S
m
m
IN
D
m
S
m
IN
GS
S
GS
m
IN
GS
GS
m
D
R
g
g
v
i
G
R
g
v
v
R
v
g
v
v
v
g
i
⋅
+
=
=
→
⋅
+
⋅
=
⋅
⋅
−
=
⋅
=
1
1
1
,
2. ROUT:
D
X
X
OUT
D
X
GS
m
D
X
X
GS
S
GS
m
GS
R
i
v
R
R
v
v
g
R
v
i
v
R
v
g
v
=
=
=
⋅
+
=
=
→
⋅
⋅
−
= 0
S
m
D
m
OUT
m
v
R
g
R
g
R
G
A
⋅
+
⋅
−
=
⋅
−
=
1

42. Set 3: Single-Stage Amplifiers
42
SM
Source Degeneration - 8
• If we ignore body effect and channel-length modulation:
S
m
D
m
v
D
OUT
S
m
m
m
R
g
R
g
A
R
R
R
g
g
G
⋅
+
⋅
−
=
→
=
⋅
+
=
1
,
1
• We Notice that as RS increases Gm becomes less dependent on gm:
S
S
m
m
m
R
R
g
g
G
s
R
s
R
1
1
lim
lim =
⋅
+
=
∞
→
∞
→
• That is for large RS: OUT
S
IN
S
IN
OUT
m
i
R
v
R
v
i
G ⋅
≈
→
≈
=
1
• Therefore, the amplifier becomes more linear when RS is large enough.
Intuitively, an increase in vIN tend to increase ID, however, the voltage
drop across RS also increases. This makes the amplifier less sensitive
to input changes, and makes ID smoother!
• The linearization is achieved at the cost of losing gain and voltage
headroom.

43. Set 3: Single-Stage Amplifiers
43
SM
Source Degeneration - 9
• We can manipulate the gain equation so the numerator is the
resistance seen at the drain node, and the denominator is the
resistance in the source path.
• The following are ID and gm of a transistor without RS.
S
m
D
S
m
D
m
v
R
g
R
R
g
R
g
A
+
−
=
⋅
+
⋅
−
=
1
1
• ID and gm of a transistor considering RS are:
• When ID is small such that RS gm<<1, Gm ≈ gm.
• When ID is large such that RS gm>>1, Gm ≈1/ RS.

44. Set 3: Single-Stage Amplifiers
44
SM
Alternative Method to Find the Output-Resistance of a
Degenerated Common-Source Amplifier

45. Set 3: Single-Stage Amplifiers
45
SM
Why Buffers?
• Common Source amplifiers needed a large load impedance to provide
a large gain.
• If the load is small but we need a large gain (can you think of an
example?) a buffer is used.
• Source-follower (common-drain) amplifiers can be used as buffers.
Ideal Buffer:
1. RIN=∞: the input current is zero; it doesn’t load the previous stage.
2. ROUT=0: No voltage drop at the output; behaves like a voltage source.
1
,
0
, =
=
∞
= V
OUT
IN
A
R
R

46. Set 3: Single-Stage Amplifiers
46
SM
Resistive Load - 1
• We will examine the Source follower amplifier with two different loads:
1. Resistive Load
2. Current Source Load
– Resistive Load:
• As shown below the output (source voltage) will follow the input (gate
voltage). We will analyze the following circuit using large-signal and
small-signal analysis.

47. Set 3: Single-Stage Amplifiers
47
SM
Resistive Load - 2
Large Signal Analysis:
• The relationship between VIN and VOUT is:
( ) ( )
( ) ( ) S
OUT
DD
TH
OUT
IN
ox
n
OUT
S
DS
TH
GS
ox
n
D
S
OUT
R
V
V
V
V
V
L
W
C
V
R
V
V
V
L
W
C
I
R
V
⋅
⋅
−
⋅
+
⋅
−
−
=
⋅
⋅
+
⋅
−
=
⋅
=
λ
λ
µ
λ
µ
1
2
1
1
2
1
2
2
( )
IN
OUT
IN
OUT
SB
F
IN
OUT
OUT
TH
IN
TH
OUT
SB
F
SB
F
TH
TH
V
V
V
V
V
V
V
V
V
V
V
V
V
V
V
V
∂
∂
⋅
=
∂
∂
⋅
+
Φ
⋅
=
∂
∂
⋅
∂
∂
=
∂
∂
=
Φ
⋅
−
+
Φ
⋅
⋅
+
=
η
γ
γ
2
2
,
2
2
0
( ) ( )
( ) ( )
IN
OUT
S
TH
GS
ox
n
S
DS
IN
TH
IN
OUT
TH
OUT
IN
ox
n
IN
OUT
V
V
R
V
V
L
W
C
R
V
V
V
V
V
V
V
V
L
W
C
V
V
∂
∂
⋅
−
⋅
⋅
−
+
⋅
⋅
+
⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∂
∂
−
∂
∂
−
⋅
−
−
=
∂
∂
λ
µ
λ
µ
2
2
1
1
1
• Differentiate with respect to VIN:
• Need to find the derivative of VTH with respect to VIN:

48. Set 3: Single-Stage Amplifiers
48
SM
Resistive Load - 3
( )
S
o
mb
m
S
m
o
S
S
mb
S
m
S
m
IN
OUT
V
S
m
S
D
S
m
S
m
IN
OUT
R
r
g
g
R
g
r
R
R
g
R
g
R
g
V
V
A
R
g
R
I
R
g
R
g
V
V
⋅
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
+
⋅
=
+
⋅
+
⋅
+
⋅
=
∂
∂
=
⋅
=
⋅
⋅
+
⋅
⋅
+
⋅
+
⋅
∂
∂
1
1
1
1 λ
η
Large Signal Analysis (Continued):
• The small signal gain can be found:
• If channel-length modulation is ignored (ro=∞) we get:
( ) S
mb
m
S
m
IN
OUT
V
R
g
g
R
g
V
V
A
⋅
+
+
⋅
=
∂
∂
=
1

49. Set 3: Single-Stage Amplifiers
49
SM
Resistive Load - 4
Small Signal Analysis:
• We get the following small signal model:
( )
( ) ( )
( )
( )
( )
1
1
1
,
,
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
+
⋅
⋅
=
+
⋅
+
⋅
+
⋅
⋅
⋅
=
⋅
⋅
+
⋅
⋅
+
+
⋅
⋅
=
=
⋅
⋅
⋅
=
⋅
⋅
+
⋅
⋅
+
+
⋅
+
⋅
⋅
−
⋅
+
−
⋅
=
−
=
−
=
⋅
⋅
+
⋅
=
mb
m
O
S
S
m
v
O
O
mb
O
m
S
O
S
m
O
S
mb
O
S
m
O
S
O
S
m
IN
OUT
v
IN
O
S
m
O
S
mb
O
S
m
O
S
OUT
O
S
O
S
OUT
mb
OUT
IN
m
OUT
OUT
BS
OUT
IN
GS
O
S
BS
mb
GS
m
OUT
g
g
r
R
R
g
A
r
r
g
r
g
R
r
R
g
r
R
g
r
R
g
r
R
r
R
g
v
v
A
v
r
R
g
r
R
g
r
R
g
r
R
v
r
R
r
R
v
g
v
v
g
v
v
v
v
v
v
r
R
v
g
v
g
v

50. Set 3: Single-Stage Amplifiers
50
SM
Resistive Load - 5
• Graph of the gain of a source-follower amplifier:
1. M1 never enters the triode region as long as VIN<VDD.
2. Gain is zero if VIN is less than VTH (because gm is 0).
3. As VIN increases, gm increases and the gain becomes:
4. As VOUT increases, η decreases, and therefore, the maximum gain
increases.
5. Even if RS=∞, the gain is less than one:
6. Gain depends heavily on the DC level of the input (nonlinear amplifier).
η
+
=
+
≈
1
1
mb
m
m
v
g
g
g
A
1
1
<
+
+
≈
o
mb
m
m
V
r
g
g
g
A

51. Set 3: Single-Stage Amplifiers
51
SM
Current Source Load
• In a source follower with a resistive load, the
drain current depends on the DC level of VIN,
which makes the amplifier highly nonlinear.
• To avoid this problem, we can use a current
source as the load.
• The output resistance is:
2
1
1
1
1
1
2
1
1
1
1
1
1
1
,
1
1
o
mb
m
o
I
M
OUT
o
I
mb
m
o
M
r
g
g
r
R
R
R
r
R
g
g
r
R =
=
→
=
=
• If channel length modulation is ignored (ro1=ro2=∞) :
1
1
1
1
1
1
1
1
1
1
1
mb
m
mb
m
mb
m
OUT
g
g
g
g
g
g
R
+
=
=
∞
∞
=
• Note that the body effect reduces the output impedance of the source
follower amplifiers.

52. Set 3: Single-Stage Amplifiers
52
SM
Voltage Division in Source Followers - 1
• When Calculating output resistance seen at the source of M1,
i.e., RM1,, we force vIN to zero and find the output impedance:
1
1
1
1
1
1
mb
m
o
M
g
g
r
R =
• However, if we were to find the gain of the amplifier, we would not
suppress vIN.
• Here, we would like to find an equivalent circuit of M1, from which we can
find the gain.
• Consider the small-signal model of M1:

53. Set 3: Single-Stage Amplifiers
53
SM
Voltage Division in Source Followers - 2
• For small-signal analysis vBS= vDS, so gmbvBS dependant current source
can be replaced by a resistor (1/gmb) between source and drain.
• Note that, when looking at the circuit from the source terminal, we can
replace the gmvGS dependant current source with a resistor (of value
1/gm) between source and gate.
• Simplified circuit:

54. Set 3: Single-Stage Amplifiers
54
SM
Voltage Division in Source Followers - 3
Example:
• Find the gain of a source follower amplifier with a resistive
load.
• We draw the small signal model of this amplifier as shown
below to get:
m
mb
O
S
mb
O
S
IN
OUT
v
IN
m
mb
O
S
mb
O
S
OUT
g
g
r
R
g
r
R
v
v
A
v
g
g
r
R
g
r
R
v
1
1
1
1
1
1
+
=
=
→
⋅
+
=
m
O
S
mb
O
S
O
S
m
O
S
m
mb
O
S
O
S
O
S
mb
O
S
O
S
O
S
m
mb
O
S
mb
O
S
v
g
r
R
g
r
R
r
R
g
r
R
g
g
r
R
r
R
r
R
g
r
R
r
R
r
R
g
g
r
R
g
r
R
A
⋅
⋅
+
⋅
⋅
+
+
⋅
⋅
=
+
⋅
⋅
+
+
⋅
⋅
⋅
+
+
⋅
=
+
+
+
+
+
=
1
1
1
1
1
1
1
1
• We can show that this is equal to what we obtained before:

55. Set 3: Single-Stage Amplifiers
55
SM
Voltage Division in Source Followers - 4
Example:
• Find the gain of a source follower amplifier with a current
source load.
• Small-signal model of this amplifier is:
1
1
1
2
1
1
2
1
1
1
2
1
1
2
1
1
1
1
1
1
m
mb
O
O
mb
O
O
IN
OUT
v
IN
m
mb
O
O
mb
O
O
OUT
g
g
r
r
g
r
r
v
v
A
v
g
g
r
r
g
r
r
v
+
=
=
→
⋅
+
=
• If we ignore channel length modulation:
1
1
1
1
1
1
1
1
1
1
1
1
m
mb
mb
IN
OUT
v
IN
m
mb
mb
OUT
g
g
g
v
v
A
v
g
g
g
v
+
=
=
→
⋅
+
=

56. Set 3: Single-Stage Amplifiers
56
SM
Voltage Division in Source Followers - 5
Example:
• Find the gain of a source follower amplifier with a resistive
load and biased with a current source.
• Small-signal model of this amplifier is:
1
1
1
2
1
1
2
1
1
1
2
1
1
2
1
1
1
1
1
1
m
mb
O
L
O
mb
O
L
O
IN
OUT
v
IN
m
mb
O
L
O
mb
O
L
O
OUT
g
g
r
R
r
g
r
R
r
v
v
A
v
g
g
r
R
r
g
r
R
r
v
+
=
=
→
⋅
+
=

57. Set 3: Single-Stage Amplifiers
57
SM
Voltage Division in Source Followers - 6
Example:
• Find the gain of a source follower amplifier with a resistive
load.
• Small-signal model of this amplifier is:
1
2
2
1
1
2
2
2
1
1
2
1
2
2
1
1
2
2
2
1
1
2
1
1
1
1
1
1
1
1
1
1
1
1
1
1
m
mb
m
mb
O
O
mb
m
mb
O
O
IN
OUT
v
IN
m
mb
m
mb
O
O
mb
m
mb
O
O
OUT
g
g
g
g
r
r
g
g
g
r
r
v
v
A
v
g
g
g
g
r
r
g
g
g
r
r
v
+
=
=
→
⋅
+
=

58. Set 3: Single-Stage Amplifiers
58
SM
Advantages and Disadvantages - 1
1. Source followers have typically small output impedance.
2. Source followers have large input impedance.
3. Source followers have poor driving capabilities..
4. Source followers are nonlinear. This nonlinearity is caused by:
¾ Variable bias current which can be resolved if we use a current
source to bias the source follower.
¾ Body effect; i.e., dependence of VTH on the source (output)
voltage. This can be resolved for PMOS devices, because each
PMOS transistor can have a separate n-well. However, because
of low mobility, PMOS devices have higher output impedance.
(In more advanced technologies, NMOS in a separate p-well,
can be implemented that potentially has no body effect)
¾ Dependence of ro on VDS in submicron devices.

59. Set 3: Single-Stage Amplifiers
59
SM
Advantages and Disadvantages - 2
5. Source followers have voltage headroom limitations due to level shift.
Consider this circuit (a common source followed by a source follower):
• If we only consider the common source stage, VX>VGS1-VTH1.
• If we only consider the source follower stage, VX>VGS3-VTH3+ VGS2.
• Therefore, adding the source follower will reduce the allowable voltage
swing at node X.
• The DC value of VOUT is VGS2 lower than the DC value of VX.

60. Set 3: Single-Stage Amplifiers
60
SM
Common-Gate
Av = (gm + gmb )RD = gm(1 + η)RD

61. Set 3: Single-Stage Amplifiers
61
SM
Common-Gate
Av =
(gm + gmb )ro +1
ro + (gm + gmb )roRS + RS + RD
RD

62. Set 3: Single-Stage Amplifiers
62
SM
Common-Gate
Av =
(gm + gmb )ro +1
ro + (gm + gmb )roRS + RS + RD
RD
)
||
)(
(
:
0 D
o
mb
m
v
S R
r
g
g
A
R +
≈
=
for

63. Set 3: Single-Stage Amplifiers
63
SM
Common-Gate Input Impedance
o
mb
m
o
o
mb
m
D
o
mb
m
o
D
in
r
g
g
r
r
g
g
R
r
g
g
r
R
R
)
(
1
)
(
1
)
(
1 +
+
+
+
+
=
+
+
+
=
)
1
||
1
||
(
)
(
1 mb
m
o
o
mb
m
D
in
g
g
r
r
g
g
R
R +
+
+
=

64. Set 3: Single-Stage Amplifiers
64
SM
Common-Gate Input Impedance
• Input impedance of common-gate stage is relatively low only if
RD is small
• Example: Find the input impedance of the following circuit.

65. Set 3: Single-Stage Amplifiers
65
SM
Example
• Calculate the voltage gain of the following circuit:
o
mb
m
v r
g
g
A )
(
1 +
+
=

66. Set 3: Single-Stage Amplifiers
66
SM
Common-Gate Output Impedance
D
S
o
S
mb
m
out R
R
r
R
g
g
R ||
}
]
)
(
1
{[ +
+
+
=

67. Set 3: Single-Stage Amplifiers
67
SM
Example
• Compare the gain of the following two circuits (λ=γ=0 and 50Ω transmission
lines!)

68. Set 3: Single-Stage Amplifiers
68
SM
Cascode Stage
D
o
o
mb
m
D
o
o
o
mb
m
out
R
r
r
g
g
R
r
r
r
g
g
R
||
]
)
[(
||
}
]
)
(
1
{[
2
1
2
2
1
2
1
2
2
+
≈
+
+
+
=
AV ≈ gm1{[ro1ro2 (gm2 + gmb2 )] || RD ]}
• Cascade of a common-source stage and a common-gate stage is called a “cascode” stage.

69. Set 3: Single-Stage Amplifiers
69
SM
Cascode Stage
AV ≈ gm1[(ro1ro2 gm2 ) || (ro3ro4gm3 )]

70. Set 3: Single-Stage Amplifiers
70
SM
Output Impedance Comparison

71. Set 3: Single-Stage Amplifiers
71
SM
Shielding Property

72. Set 3: Single-Stage Amplifiers
72
SM
Board Notes

73. Set 3: Single-Stage Amplifiers
73
SM
Triple Cascode
• What is the output resistance of this circuit?
• Problem?

74. Set 3: Single-Stage Amplifiers
74
SM
Folded Cascode

75. Set 3: Single-Stage Amplifiers
75
SM
Output Impedance of a Folded Cascode
2
3
1
2
2
2 )
||
](
)
(
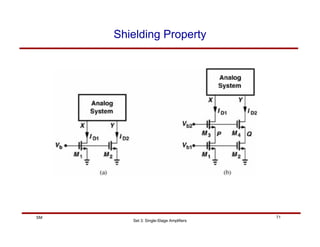
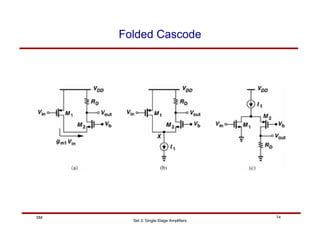
1
[ o
o
o
o
mb
m
out r
r
r
r
g
g
R +
+
+
=