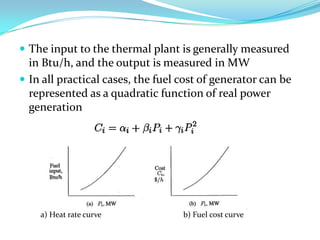
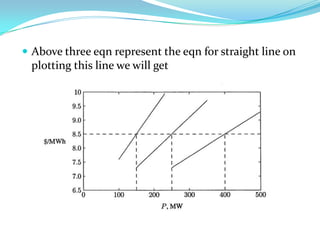
This document presents an overview of economic load dispatch in power systems. It discusses the objectives of economic dispatch as generating required power at minimum cost. It describes different constraints like generator limits, transmission limits and voltage limits that need to be considered. It explains the operating costs of thermal plants using heat rate and fuel cost curves. It provides formulations for economic dispatch neglecting and including transmission losses. The document uses examples to illustrate the iterative method used to solve economic dispatch problems.

1. PRESENTED BY
DEEPAK JOHN
S1 M. Tech
POWER SYSTEM

2. CONTENTS
 INTRODUCTION
 DIFFERENT CONSTRAINTS IN ECONOMIC LOAD
DISPATCH
 OPERATING COST OF THERMAL PLANT
 ECONOMIC DISPATCH NEGLECTING
LOSSES
 ECONOMIC DISPATCH INCLUDING
LOSSES
 REFERENCES

3. INTRODUCTION
 In power generation our main aim is to generate the
required amount of power with minimum cost.
 Economic load dispatch means that the generator’s
real and reactive power are allowed to vary within
certain limits so as to meet a particular load demand
with minimum fuel cost
 This allocation of loads are based on some
constraints.

4. DIFFERENT CONSTRAINTS IN
ECONOMIC LOAD DISPATCH
 INEQUALITY CONSTRAINTS
 Voltage constraints
Vmin ≤ V ≤ Vmax ,
δmin ≤ δ ≤ δmax
 Generator constraints
KVA loading of generator should not exceed prescribed
value
Pmin ≤ P ≤ Pmax
Qmin ≤ Q ≤ Qmax

5.  Running spare capacity constraints
This constraints are needed to meet forced outage of
one or more alternators in the system and also
unexpected load on the system
 Transmission line constraints
flow of power through transmission line should less
than its thermal capacity
 Transformer tap set
for autotransformer tap t should between 0 & 1
For two winding transformer – between 0& k

6.  Equality constraints
 Real power
Pp= Vp Σ Ypq Vq cos(θpq-(δp+δq))
 Reactive power
Qp= Vp Σ Ypq Vq sin(θpq-(δp+δq))

7. OPERATING COST OF THERMAL
PLANT
 The factors influencing power generation at minimum
cost are operating efficiencies of generators, fuel
cost, and transmission losses.
 The most efficient generator in the system does not
guarantee minimum cost as it may be located in an
area where fuel cost is high.
 If the plant is located far from the load
center, transmission losses may be considerably higher
and hence the plant may be overly uneconomical.

8.  The input to the thermal plant is generally measured
in Btu/h, and the output is measured in MW
 In all practical cases, the fuel cost of generator can be
represented as a quadratic function of real power
generation
a) Heat rate curve b) Fuel cost curve

9. Incremental fuel-cost curve
• By plotting the derivative of the fuel-cost curve versus
the real power we get the incremental fuel-cost curve
The incremental fuel-cost curve is a measure of how
costly it will be to produce the next increment of
power.

10. ECONOMIC DISPATCH NEGLECTING
LOSSES
 It is the simplest economic dispatch problem
 Assume that the system is only one bus with all
generation and loads connected to it
 A cost function Ci is assumed to be known for each
plant

11.  The problem is to find the real power generation for
each plant such that the objective function (i.e., total
production cost) as defined by the equation
Is minimum ,subjected to the constraints

14.  when losses are neglected with no generator limits, for
most economic operation. all plants must operate at
equal incremental production cost
 Production from each plant can be found by
This equation is known as the coordination equation
For analytic solution we can find λ by

15.  In an iterative technique, starting with a value of λ and
the process is continued until ∆Pi is within a specified
accuracy
 Corresponding to this λ ,
is calculated, and the power mismatch is calculated by
Update value of λ by

16. EXAMPLE

18.  Above three eqn represent the eqn for straight line on
plotting this line we will get

21. ECONOMIC DISPATCH INCLUDING
LOSSES
 When power is transmitted over long distances
transmission losses are a major factor that affect the
optimum dispatch of generation
 One common practice for including the effect of
transmission losses is to express the total transmission loss
as a quadratic function of the generator power outputs. The
simplest quadratic form is

23. Using the langrange multiplier
Minimum of this function is fount at the points where the
partials of the function to it’s variables are zero

25. Itration method
Initially assume a λ value. Then find out the generation
from each plant using the equation
Calculate the power mismatch
calculate

26. Update value of λ
Repeat the procedure with new value of λ until the
power mismatch is within the limit

27. EXAMPLE

28. SOLUTION

35. REFERENCES
 Power System Analysis - Hadi Saadat
 power system analysis by nagrath and kothari

36. THANKS