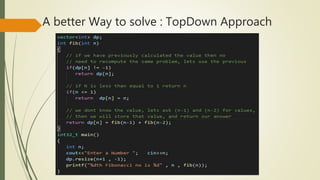
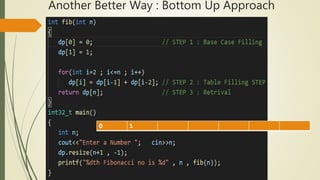
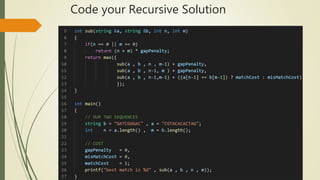
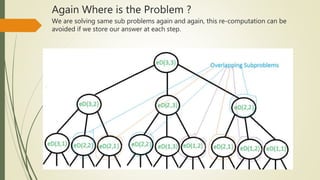
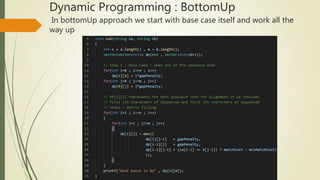
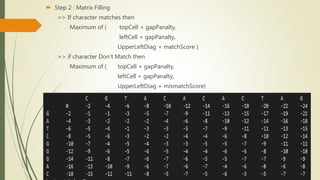
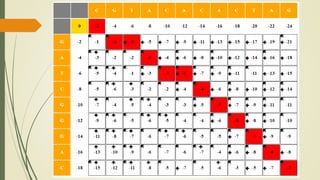
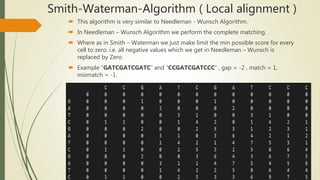
Dynamic programming can be used to solve the sequence alignment problem of finding the optimal cost of aligning two sequences. It avoids recomputing the same subproblems as recursion by storing the results in a 2D table. The Needleman-Wunsch algorithm uses a bottom-up dynamic programming approach to fill the table and find the optimal alignment cost between the sequences. It then traces back through the table to retrieve the optimal alignment. The Smith-Waterman algorithm is similar but limits scores to be non-negative to find local rather than global alignments.

1. Dynamic Programming :
Sequence Alignment
Rohan Prakash
2K17 / BT / 20

2. Flow of Presentation
What is Dynamic Programming
Example : Fibonacci Number
TopDown and BottomUp Dynamic Programming
Sequence alignment – best possible cost
Recursive / Dynamic approach ( Needleman – Wunsch )
Sequence alignment optimal Traceback
Smith Waterman ( brief )

3. What is Dynamic Programming
 Dynamic Programming is just an optimization over a plain Recursion.
 If the Recursive solution to a problem has repeating sub problems then
we can avoid the recalculation of same sub problems.

4. Fibonacci Number
 Suppose we have a simple problem –
Q : Given a integer ‘n’ calculate the nth Fibonacci number. Fibonacci series goes
like 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …… ,
Simple recursive Solution :
F(n) = F(n-1) + F(n-2)

5. Where is the problem ? What's the need
for Dynamic Programming ?
 Time Complexity of recursive call is Exponential. We are calculating same sub
problems again and again.
 Here is the recursion Tree for 6th Fibonacci Number

6. A better Way to solve : TopDown Approach

7. BottomUp Dynamic Programming
 Start from the base case and build all the way up to the required solution
0 1
0 1 2 3 4 5 6

8. Another Better Way : Bottom Up Approach
0 1

9. Best Possible Cost of Sequence Alignment ?
 Q : Given two Sequences, find the cost of aligning the two sequences, if we allow different cost for
mismatches , matches and gap
Example : what is the best possible cost for aligning the two sequences
“GATCGGGAC” to “CGTACACACTAG” given the following cost
gapPanalty = 0 ,
mismatch = 0 and
match = 1
Output = “best possible cost is 5”

10. Logic Building for Recursive solution
 Base Case : What is one of the sequence is empty ?
=> then return the length of other sequence * gapPanalty
 If a particular character does not matches then what should we do ?
=> we should look at the following cost , cost of adding a gap in 1st sequence , cost of
adding a gap in second sequence , and cost of mismatch.
=> Then go with the one that gives the maximum cost
 What is a particular character matches , what should the program do ?
=> we should look at the following cost ,
 cost of extending 1st sequence (i.e. adding gap in 2nd ),
 cost of extending 2nd sequence (i.e. adding gap in 1st )
 cost of extending both the sequences
=> Then go with the one that gives the maximum cost

11. Code your Recursive Solution

12. Again Where is the Problem ?
We are solving same sub problems again and again, this re-computation can be
avoided if we store our answer at each step.

13. Dynamic Programming : TopDown

14. Dynamic Programming : BottomUp
In bottomUp approach we start with base case itself and work all the
way up

15. How our DP table looks like :
sequenceA = GATCGGGAC , sequenceB = CGTACACACTAG
MatchScore = 1
MisMatchScore = -1
GapScore = -2
 Step 1 : Base case Filling

16.  Step 2 : Matrix Filling
=> If character matches then
Maximum of ( topCell + gapPanalty,
leftCell + gapPanalty,
UpperLeftDiag + matchScore )
=> if character Don’t Match then
Maximum of ( topCell + gapPanalty,
leftCell + gapPanalty,
UpperLeftDiag + mismatchScore)

18. How do we TraceBack ?
 Start From Nth row Mth column , i.e. the last cell and
 If characters matches then record characters in both the sequences
 and move to upperLeftDiagonal DP(i-1 , j-1)
 Else Check for the maxScoreamong left , top , upperLeftDiagonal
If we have max score in Left cell then add the character in sequence2 ( horizontal one ) and add
gap in sequence1 ( vertical one )
If we have max score in Top cell then add the character in sequence1 ( Vertical one ) and add
gap in sequence2 ( horizontal one )
If we have max score in Diagonal Then add corresponding characters in both the sequences
this is our Mismatch

19. Traceback

20. More Improvement ….
Scoring Matrix :
Purines ( adenine and guanine ) are chemically Similar , and
Pyrimidines ( Thymine and cytosine ) are also similar , so
different mismatch/penalty Scores should be given.

21. Smith-Waterman-Algorithm ( Local alignment )
 This algorithm is very similar to Needleman - Wunsch Algorithm.
 In Needleman – Wunsch Algorithm we perform the complete matching.
 Where as in Smith – Waterman we just make limit the min possible score for every
cell to zero. i.e. all negative values which we get in Needleman – Wunsch is
replaced by Zero.
 Example “GATCGATCGATC” and “CCGATCGATCCC” , gap = -2 , match = 1,
mismatch = -1.

22. Quick Recap
 How to Write recursive code
 Base case + Recursion logic
 Fibonacci Example
 What are subProblems
 How to avoid re-computations by storing answers to subProblems
 TopDown dynamic programming
 Check if previously calculated + RECURSION ( Base Case + Recursion Logic )
 BottomUp dynamic programming
 Start with base case itself and work all the way up
 Cost of optimal Sequence alignment Problem
 Recursion
 TopDown Dynamic Programming
 BottomUp Dynamic Programming

23.  Sequence Alignment Problem
 BottomUp Dynamic Programming
 Traceback
 Improvement – Scoring matrix for purines and pyrimidines
 Smith Waterman ( brief )

24. Thank You
Rohan Prakash 2k17/BT/20