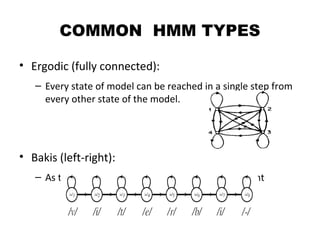
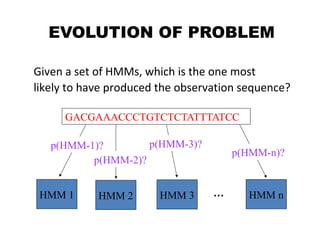
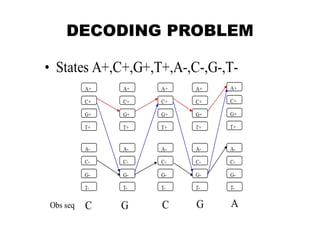
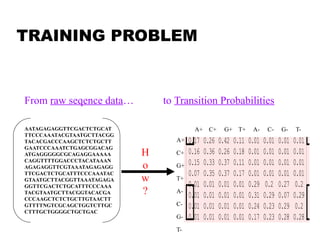
This document provides an introduction to hidden Markov models (HMMs). It discusses that HMMs can be used to model sequential processes where the underlying states cannot be directly observed, only the outputs of the states. The document outlines the basic components of an HMM including states, transition probabilities, emission probabilities, and gives examples of HMMs for coin tossing and weather. It also briefly discusses the history of HMMs and their applications in fields like bioinformatics for problems such as gene finding.

1. INTRODUCTION OF HIDDEN
MARKOV MODEL
Mohan Kumar Yadav
M.Sc Bioinformatics
JNU JAIPUR

2. HIDDEN MARKOV MODEL(HMM)
Real-world has structures and processes which have
observable outputs.
– Usually sequential .
– Cannot see the event producing the output.
Problem: how to construct a model of the structure or
process given only observations.

3. HISTORY OF HMM
• Basic theory developed and published in 1960s and 70s
• No widespread understanding and application until late
80s
• Why?
– Theory published in mathematic journals which were
not widely read.
– Insufficient tutorial material for readers to understand
and apply concepts.

4. Andrei Andreyevich Markov
1856-1922
Andrey Andreyevich Markov was a Russian
mathematician.
He is best known for his work on stochastic
processes.
A primary subject of his research later became
known as Markov chains and Markov processes .

5. HIDDEN MARKOV MODEL
• A Hidden Markov Model (HMM) is a statical model in
which the system is being modeled is assumed to be
a Markov process with hidden states.
• Markov chain property: probability of each
subsequent state depends only on what was the
previous state.

6. EXAMPLE OF HMM
• Coin toss:
– Heads, tails sequence with 2 coins
– You are in a room, with a wall
– Person behind wall flips coin, tells result
– Coin selection and toss is hidden
– Cannot observe events, only output (heads, tails) from events
– Problem is then to build a model to explain observed
sequence of heads and tails.

7. EXAMPLE OF HMM
• Weather
– Once each day weather is observed
– State 1: rain
– State 2: cloudy
– State 3: sunny
– What is the probability the weather for the next 7 days will be:
– sun, sun, rain, rain, sun, cloudy, sun
– Each state corresponds to a physical observable event

8. HMM COMPONENTS
• A set of states (x’s)
• A set of possible output symbols (y’s)
• A state transition matrix (a’s)
– probability of making transition from one state to the
next
• Output emission matrix (b’s)
– probability of a emitting/observing a symbol at a
particular state
• Initial probability vector
– probability of starting at a particular state
– Not shown, sometimes assumed to be 1

9. EXAMPLE OF HMM
0.3
0.7
Rain
Dry
0.2
• Two states : ‘Rain’ and ‘Dry’.
• Transition probabilities: P(‘Rain’|‘Rain’)=0.3 ,
P(‘Dry’|‘Rain’)=0.7 , P(‘Ra’)=0.6 .
• in’|‘Dry’)=0.2, P(‘Dry’|‘Dry’)=0.8
• Initial probabilities: say P(‘Rain’)=0.4 , P(‘Dry
0.8

10. CALCULATION OF HMM

11. HMM COMPONENTS

12. COMMON HMM TYPES
• Ergodic (fully connected):
– Every state of model can be reached in a single step from
every other state of the model.
• Bakis (left-right):
– As time increases, states proceed from left to right

13. HMM IN BIOINFORMATICS
• Hidden Markov Models (HMMs) are a
probabilistic model for modeling and
representing biological sequences.
• They allow us to do things like find genes, do
sequence alignments and find regulatory
elements such as promoters in a principled
manner.

14. PROBLEMS OF HMM
• Three problems must be solved for HMMs to be
useful in real-world applications
●
1) Evaluation
●
2) Decoding
●
3) Learning

15. EVOLUTION OF PROBLEM
Given a set of HMMs, which is the one most
likely to have produced the observation sequence?
GACGAAACCCTGTCTCTATTTATCC
p(HMM-3)?
p(HMM-1)?
p(HMM-2)?
HMM 1
HMM 2
HMM 3
p(HMM-n)?
…
HMM n

16. DECODING PROBLEM

17. TRAINING PROBLEM
From raw seqence data…
AATAGAGAGGTTCGACTCTGCAT
TTCCCAAATACGTAATGCTTACGG
TACACGACCCAAGCTCTCTGCTT
GAATCCCAAATCTGAGCGGACAG
ATGAGGGGGCGCAGAGGAAAAA
CAGGTTTTGGACCCTACATAAAN
AGAGAGGTTCGTAAATAGAGAGG
TTCGACTCTGCATTTCCCAAATAC
GTAATGCTTACGGTTAAATAGAGA
GGTTCGACTCTGCATTTCCCAAA
TACGTAATGCTTACGGTACACGA
CCCAAGCTCTCTGCTTGTAACTT
GTTTTNGTCGCAGCTGGTCTTGC
CTTTGCTGGGGCTGCTGAC
to Transition Probabilities


A+ C+
A+
H
o
w
?
C+
G+
T+
ACGT-
0.17
0.16
0.15
0.07
0.01
0.01
0.01
0.01
0.26
0.36
0.33
0.35
0.01
0.01
0.01
0.01
G+ T+
0.42
0.26
0.37
0.37
0.01
0.01
0.01
0.01
0.11
0.18
0.11
0.17
0.01
0.01
0.01
0.01
A-
C-
G-
T-
0.01
0.01
0.01
0.01
0.29
0.31
0.24
0.17
0.01
0.01
0.01
0.01
0.2
0.29
0.23
0.23
0.01
0.01
0.01
0.01
0.27
0.07
0.29
0.28
0.01
0.01
0.01
0.01
0.2
0.29
0.2
0.28



18. HMM-APPLICATION
• DNA Sequence analysis
• Protein family profiling
• Predprediction
• Splicing signals prediction
• Prediction of genes
• Horizontal gene transfer
• Radiation hybrid mapping, linkage analysis
• Prediction of DNA functional sites.
• CpG island

19. HMM-APPLICATION
• Speech Recognition
• Vehicle Trajectory Projection
• Gesture Learning for Human-Robot Interface
• Positron Emission Tomography (PET)
• Optical Signal Detection
• Digital Communications
• Music Analysis

20. HMM-BASED TOOLS
• GENSCAN (Burge 1997)
• FGENESH (Solovyev 1997)
• HMMgene (Krogh 1997)
• GENIE (Kulp 1996)
• GENMARK (Borodovsky & McIninch 1993)
• VEIL (Henderson, Salzberg, & Fasman 1997)

21. BIOINFORMATICS RESOURCES
• PROBE www.ncbi.nlm.nih.gov/
• BLOCKS www.blocks.fhcrc.org/
• META-MEME
www.cse.ucsd.edu/users/bgrundy/metameme.1.0.html
• SAM
www.cse.ucsc.edu/research/compbio/sam.html
• HMMERS hmmer.wustl.edu/
• HMMpro www.netid.com/
• GENEWISE www.sanger.ac.uk/Software/Wise2/
• PSI-BLAST www.ncbi.nlm.nih.gov/BLAST/newblast.html
• PFAM www.sanger.ac.uk/Pfam/

22. Refrences
• Rabiner, L. R. (1989). A Tutorial on Hidden Markov
Models and Selected Applications in Speech
Recognition. Proceedings of the IEEE, 77(2), 257-285.
• Essential bioinformatics, Jin Xion
• http://www.sociable1.com/v/Andrey-Markov108362562522144#sthash.tbdud7my.dpuf

23. Thank You!