This document provides an introduction to the topics covered in the Digital Signal Processing course BEG4103. It discusses discrete-time signals and systems, the Fourier transform of discrete-time signals, the discrete Fourier transform, the z-transform, and digital filters. It also provides examples of analogue and discrete-time signals and highlights both the advantages and disadvantages of digital signal processing.

1. BEG4103 Section 1 1
BEG4103:
Digital Signal Processing
ojuma@mku.ac.ke
Section 1: Introduction

2. 2
Discrete-time signals and systems: Discrete–time sequences, Linear Time
Invariant (LTI) systems, linearity, time invariance, causality, stability, unit-sample
response. Linear constant-coefficient difference equations; recursive and non-
recursive.
Fourier Transform of discrete-time signals: Definition and properties of the
Fourier Transforms, Fourier Transforms of special sequences, use of the Fourier
Transform in signal processing, inverse Fourier Transform. Sampling of continuous-
time signals.
The Discrete Fourier Transform: Definition of the Discrete Fourier Transform
(DFT), computing the DFT from the discrete-time sequence, properties of DFT,
circular and linear convolution, Fast Fourier Transform (FFT), decimation-in-time
and decimation-in-frequency FFTs.
The z-Transform: Definition of the z-transform and the region of convergence, the
z-transform theorems and properties. The system function and stability.
Relationship between the Fourier Transform and the z-transform. The inverse z-
transform.
Digital Filters: Digital filter structures, Infinite Impulse Response (IIR) filters,
impulse invariance, bilinear transformation, frequency transformations, Finite
Impulse Response (FIR) filters, Windowing method, DFT method, Frequency-
sampling method.

3. 3
•

4. 4
•

5. 5
• Analogue signals: continuous functions of time (t) measured in
seconds. Exist for all values of t in range - to +.
• Examples:
(i) 5sin(62.82t) : sine-wave of frequency 62.82 radians/second ( 10 Hz)
 0 : t < 0
(ii) u(t) =  " step-function " signal.
 1 : t  0
• Graph of analogue signal against time gives continuous 'waveform' :
t
Voltage
0.1
-0.1
5
t
Voltage
1

6. 6
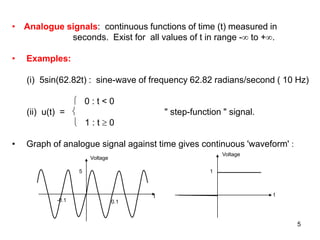
• Discrete-time signals: exist only at discrete points in time.
• Often obtained by sampling an analogue signal,
i.e. measuring its value at discrete points in time.
• Sampling points separated by equal intervals of T seconds.
• Given analogue signal x(t), x[n] = value of x(t) when t = nT.
• Sampling process produces a sequence of numbers:
{ ..., x[-2], x[-1], x[0], x[1], x[2], ..... }
• Referred to as {x[n]} or ' the sequence x[n] '.
• Sequence exists for all integer n in the range - to .

7. 7
Advantages of DSP:
• More & more signals are being transmitted & stored in digital form so
it makes sense to process them in digital form also.
• DSP systems can be designed & tested in simulation using PCs.
• Accuracy pre-determined by word-length & sampling rate.
• Reproducible as every copy of DSP system will perform identically.
• Characteristics of system will not drift with temperature or ageing.
• Availability of advanced VLSI technology.
• DSP systems can be reprogrammed without changing hardware.
• Products can be updated via Internet.
• DSP systems can perform functions that would be extremely difficult
or impossible in analogue form; e.g.
adaptive filtering
speech recognition.

8. 8
Disadvantages of digital signal processing:
• DSP designs can be expensive especially for high bandwidth signals
where fast analogue/digital conversion is required.
• Design of DSP systems can be extremely time-consuming & a highly
complex and specialised activity. There is an acute shortage of
computer science and electrical engineering graduates with the
knowledge and skill required.
• Power requirements for digital processing can be high, thus making it
unsuitable for battery powered portable devices. Fixed point
processing devices are available which are simpler than floating point
devices and less power consuming. However the ability to program
such devices is a particularly valued and difficult skill.