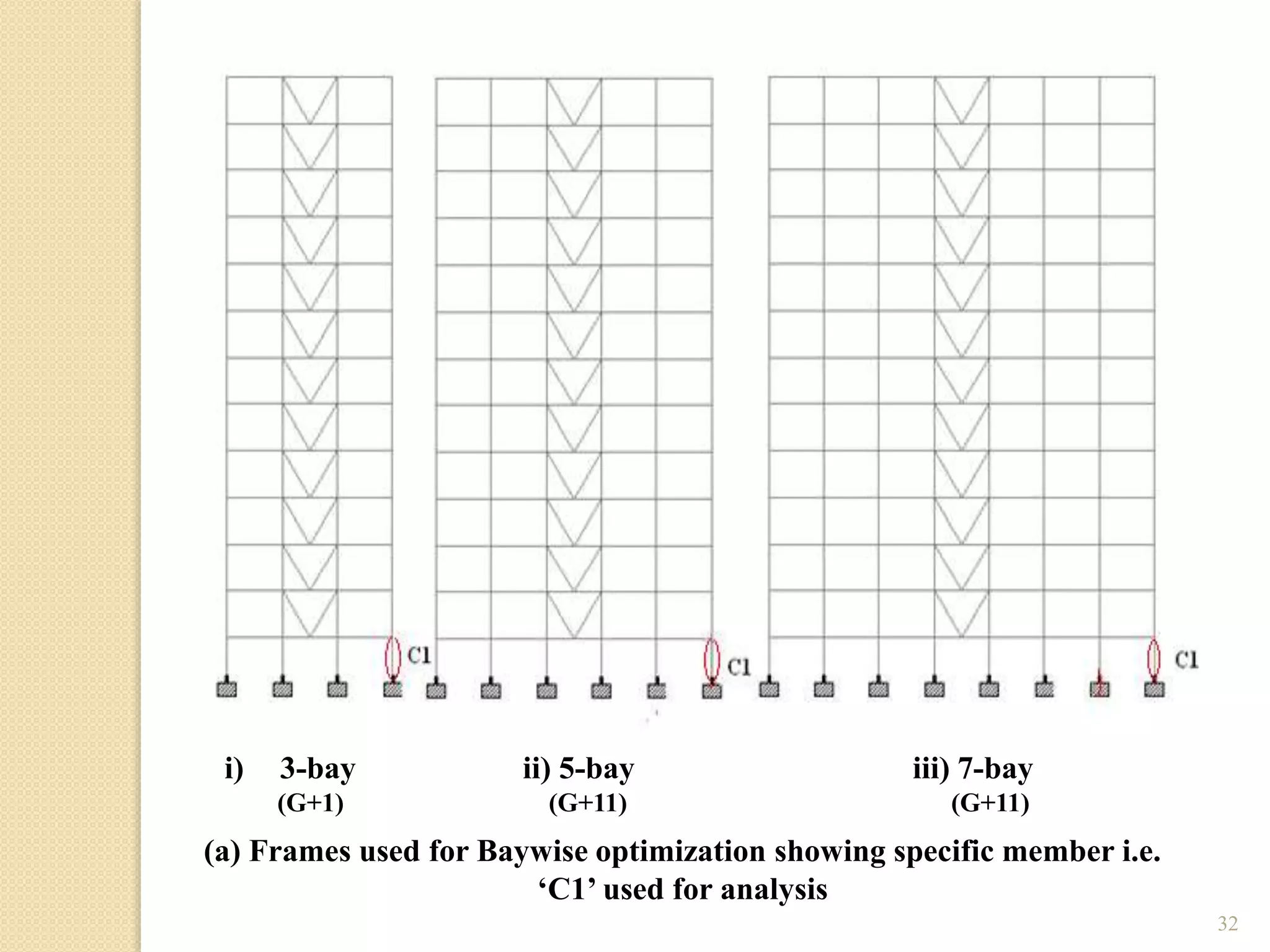
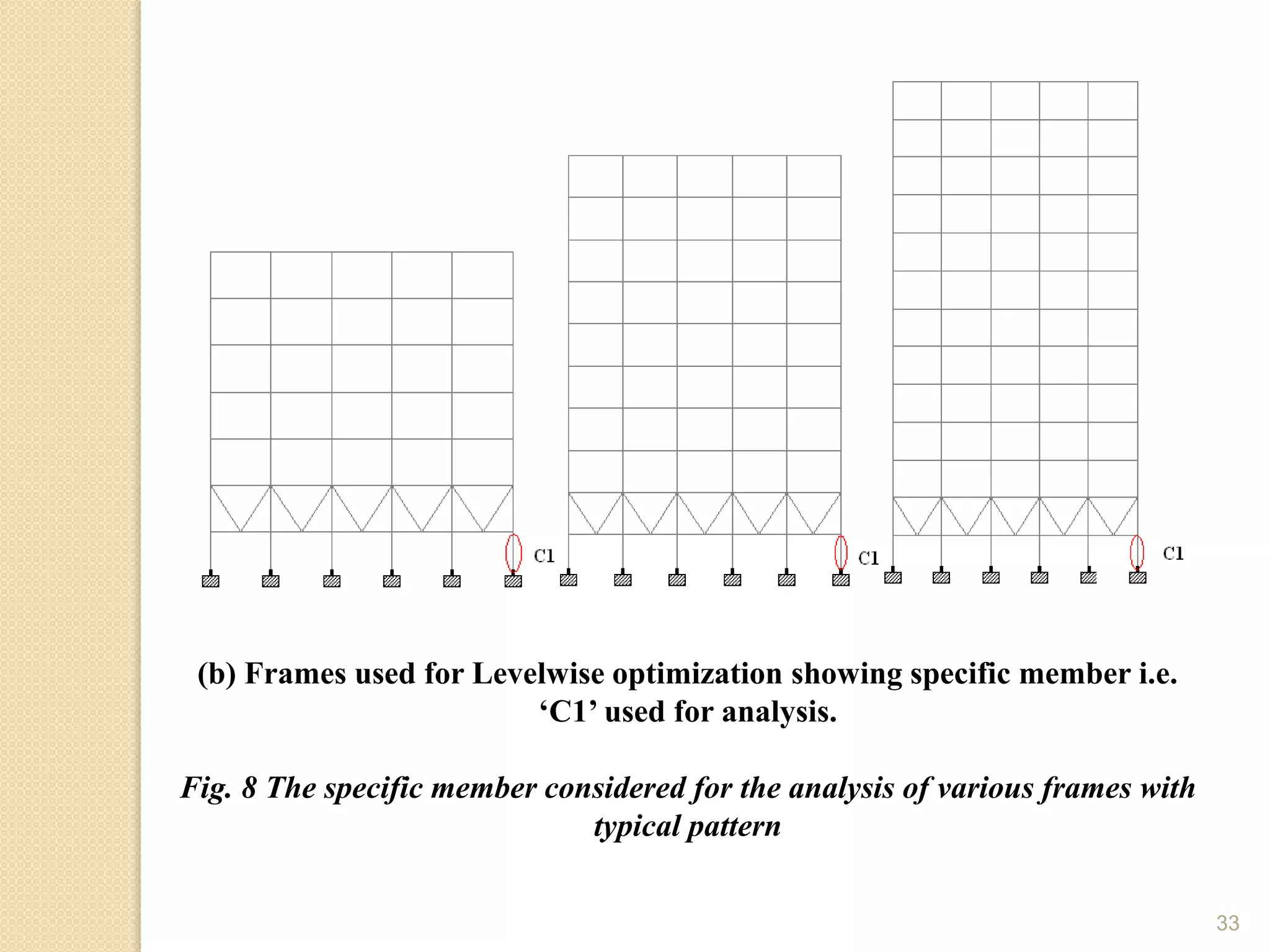
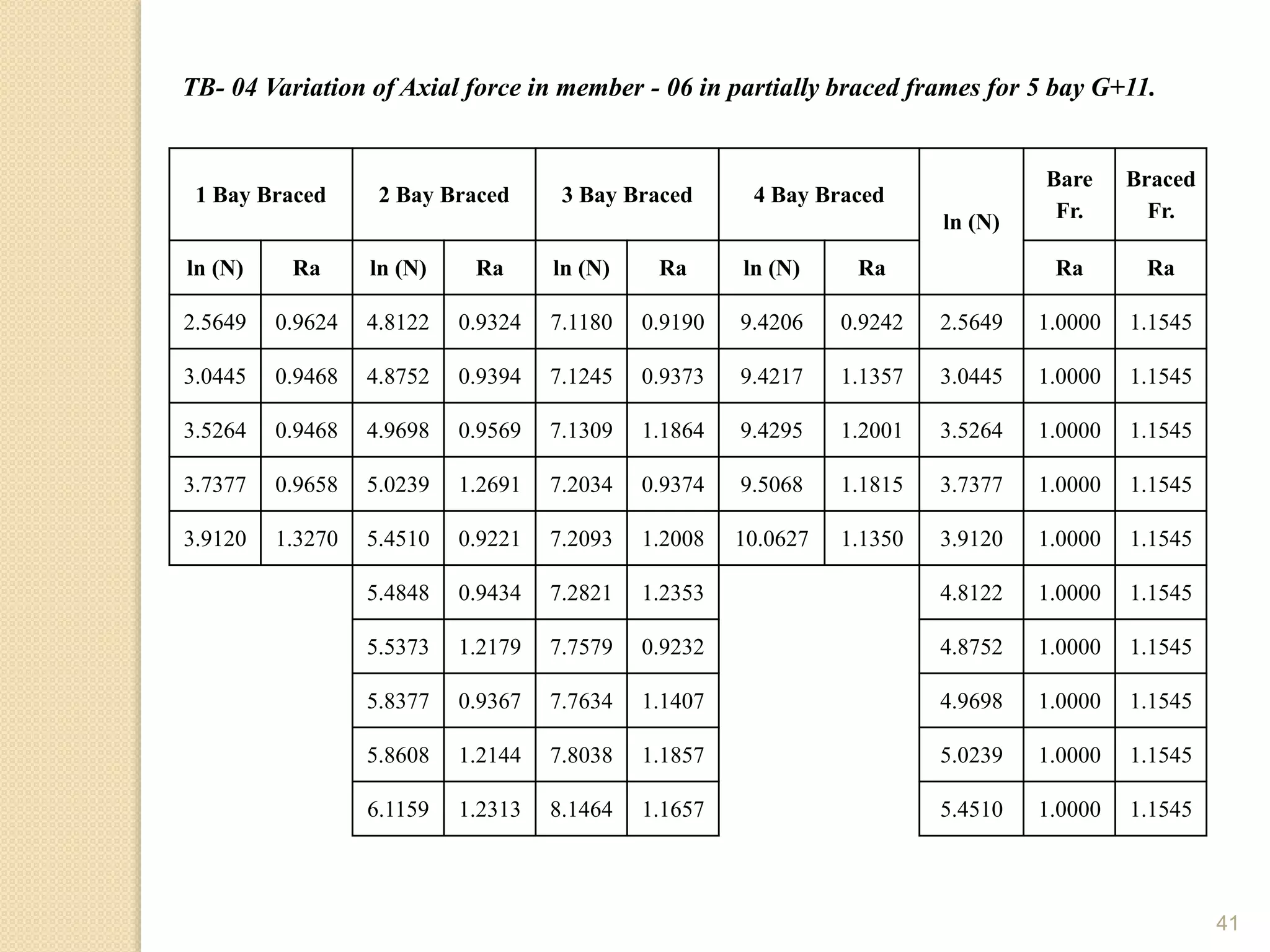
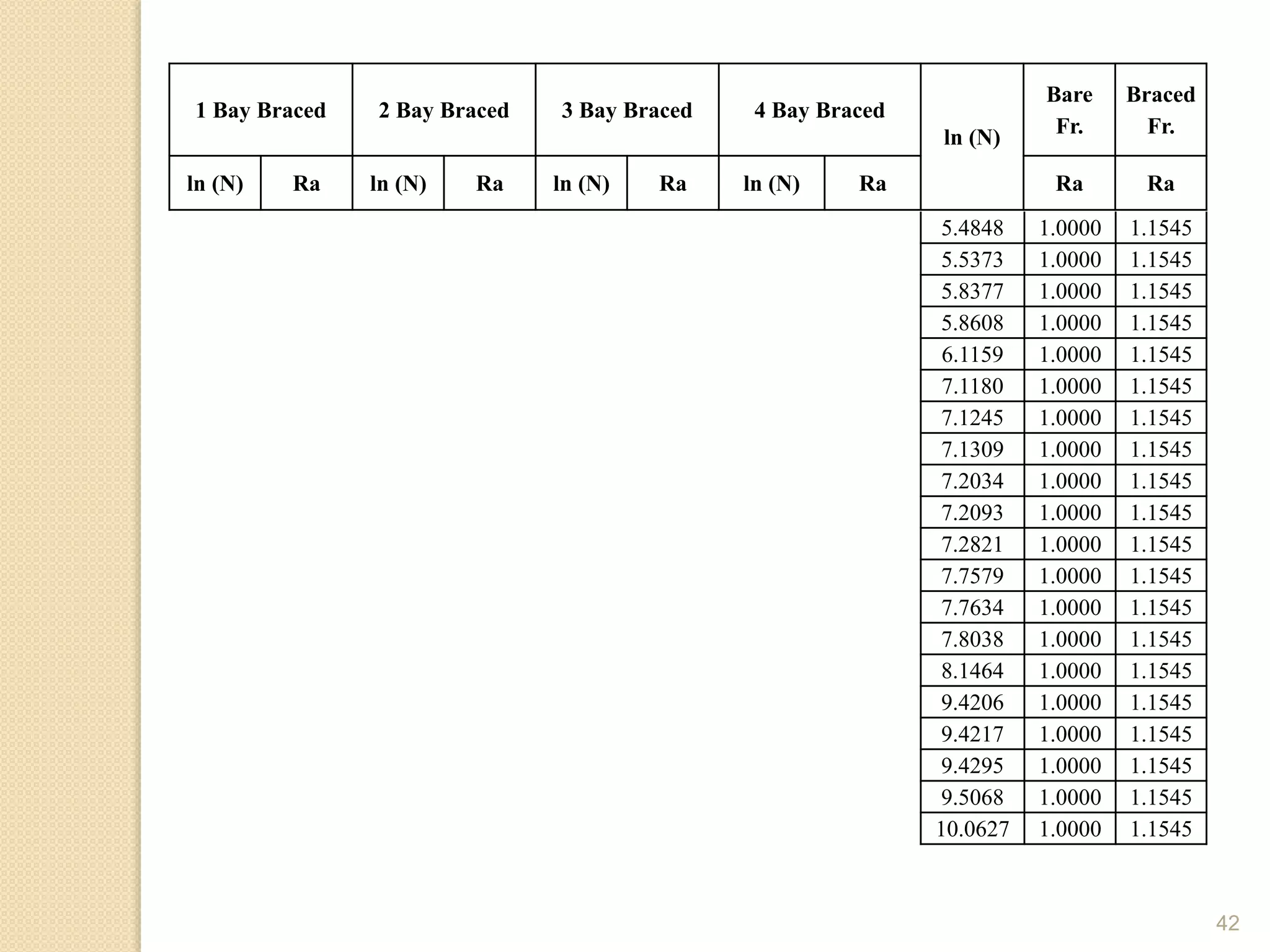
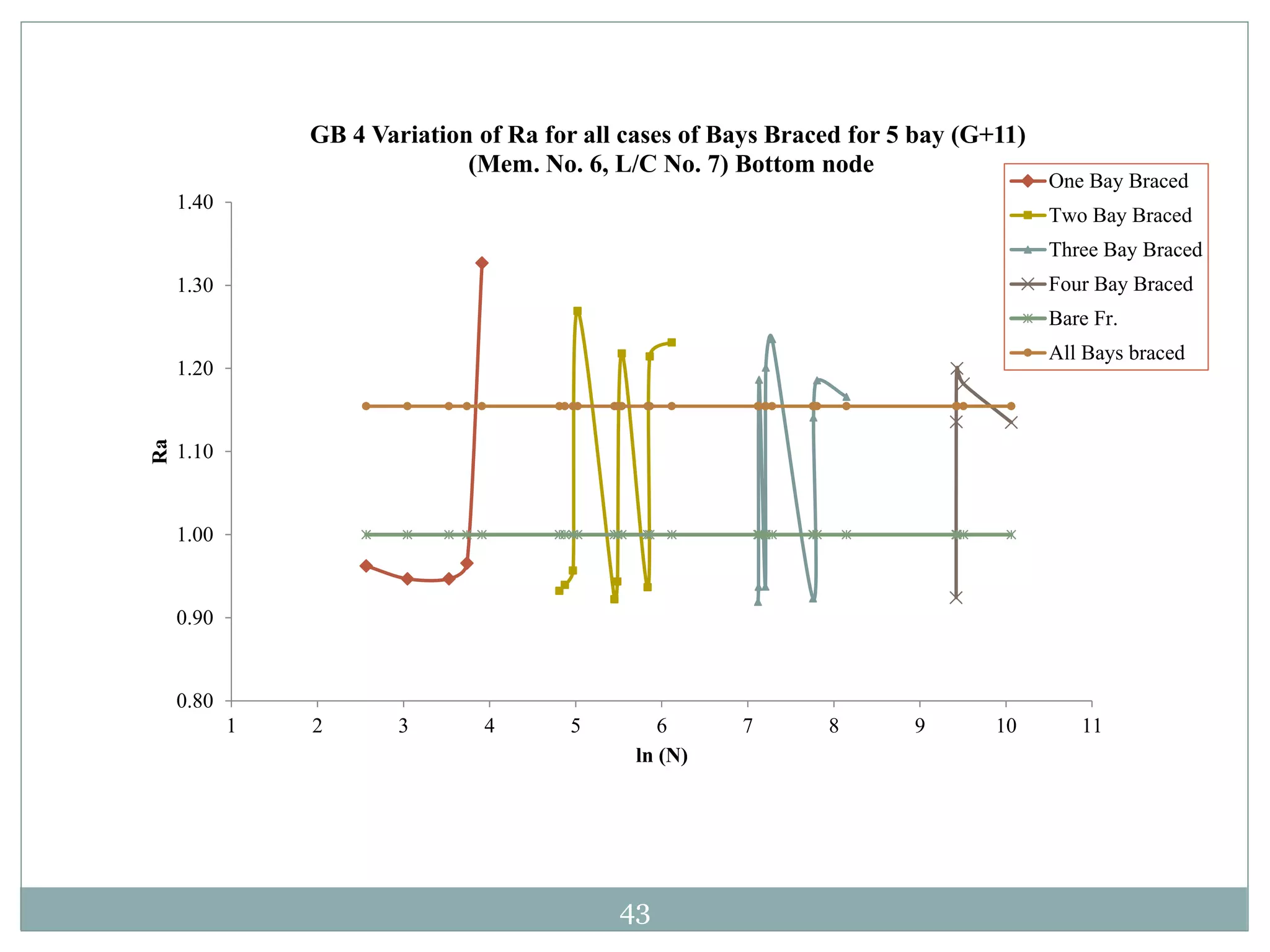
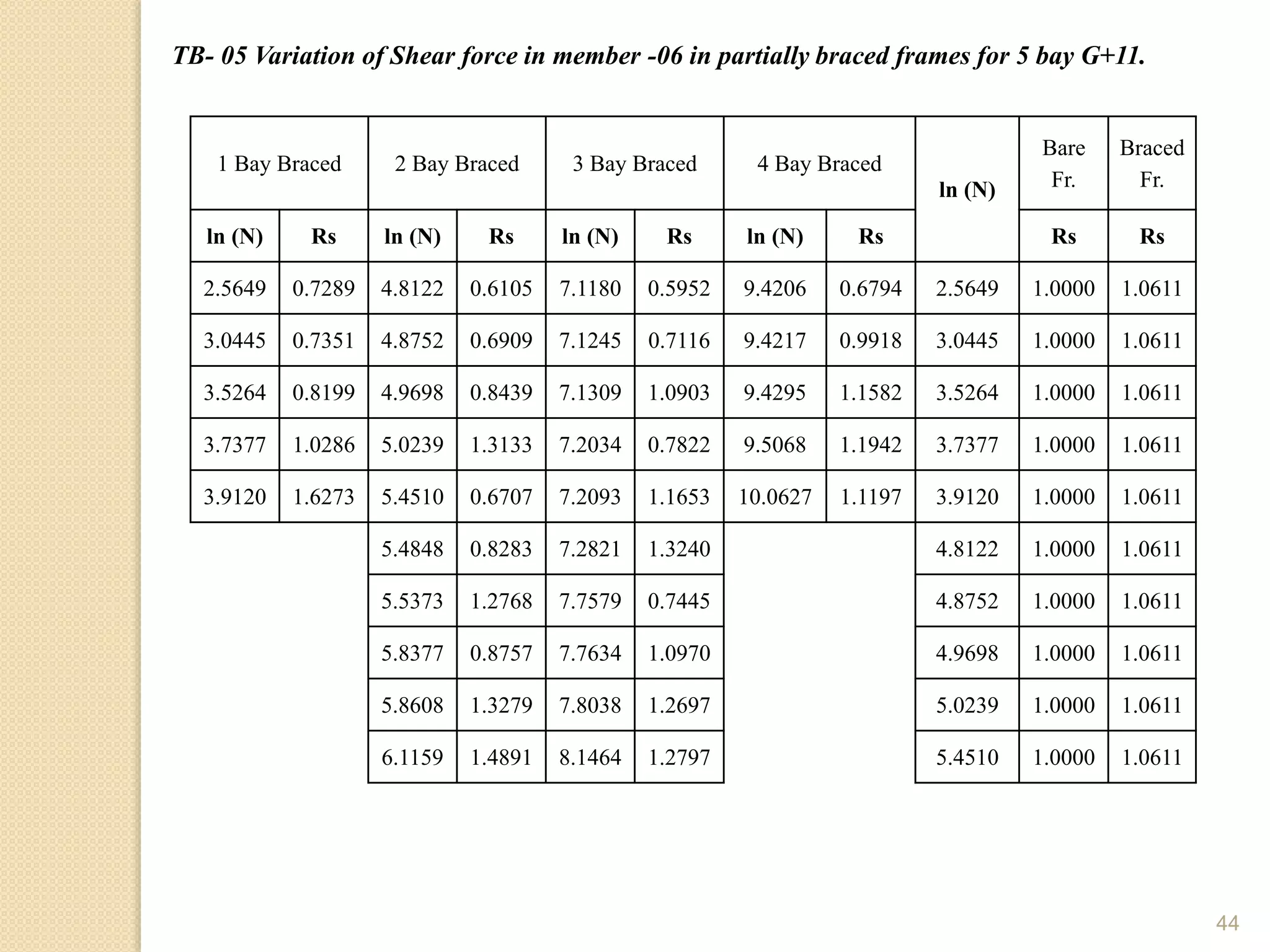
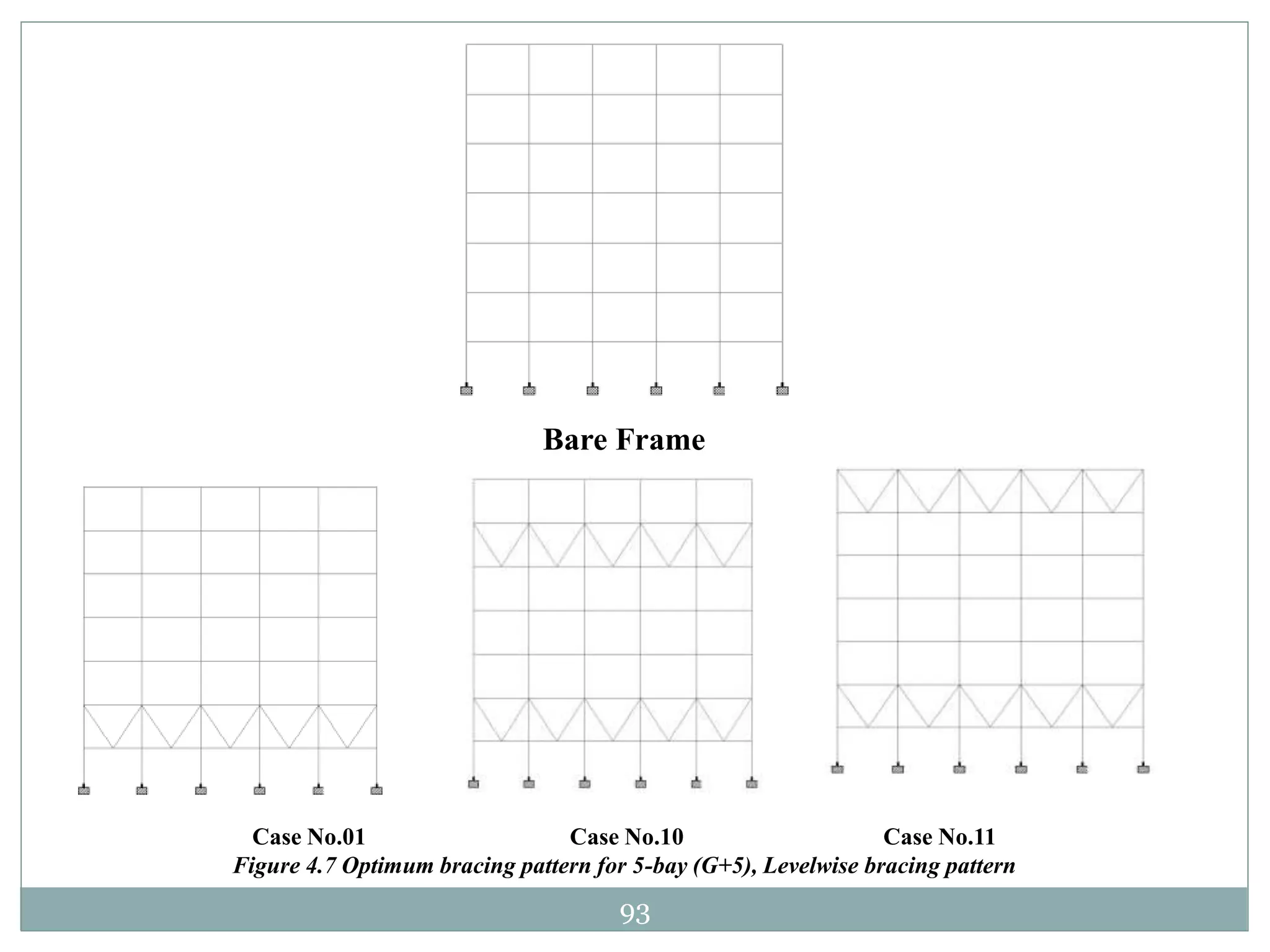
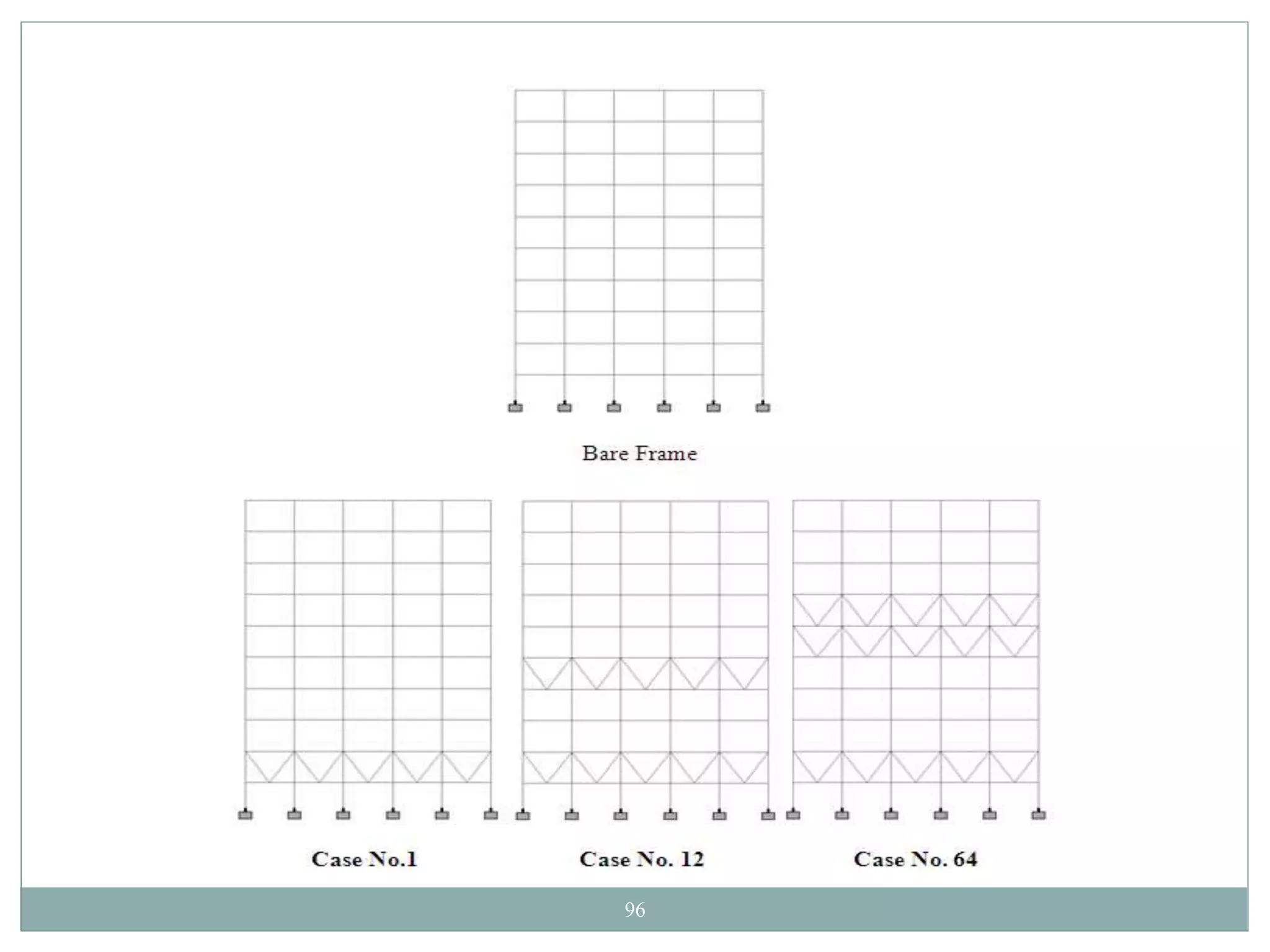
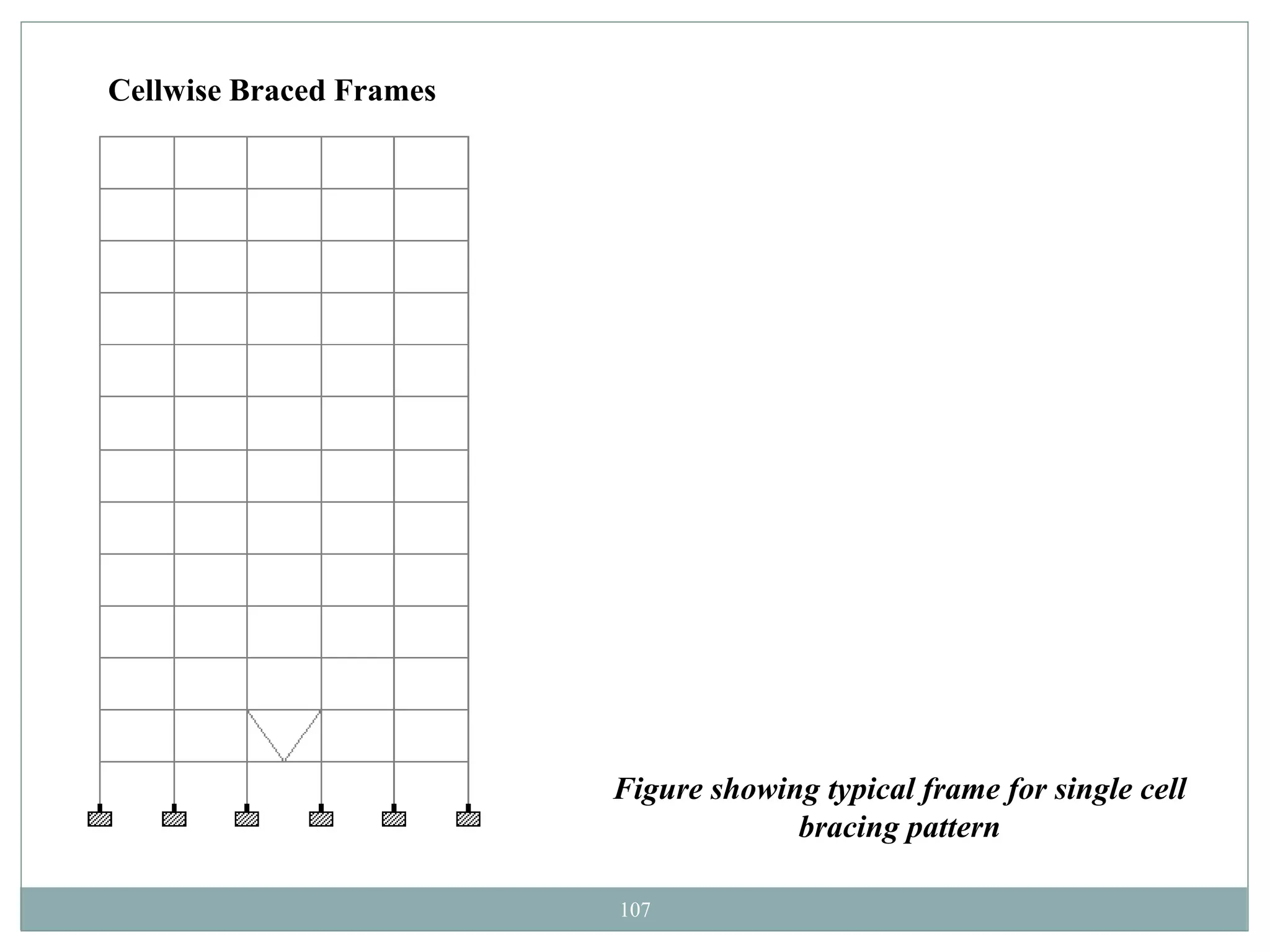
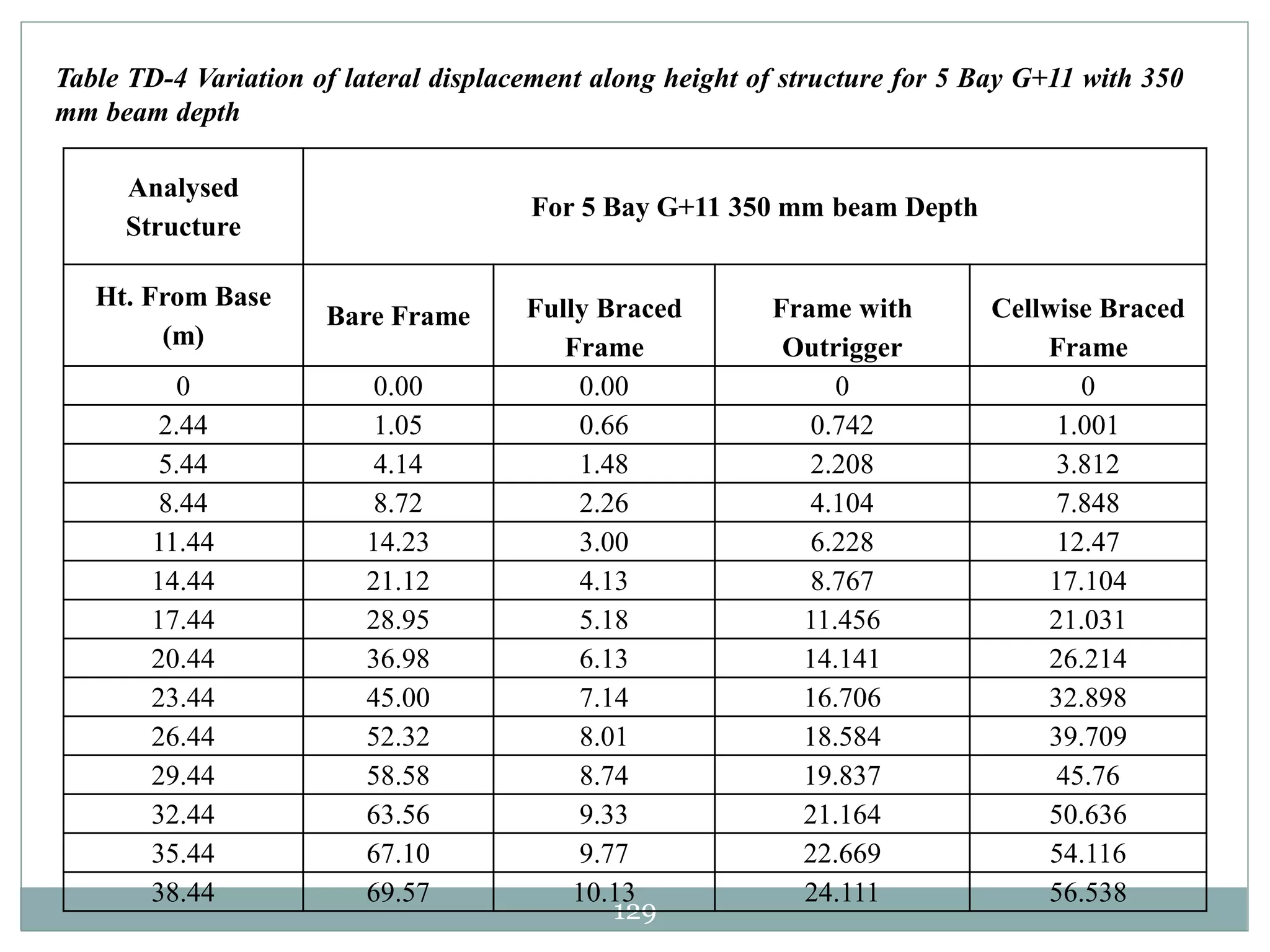
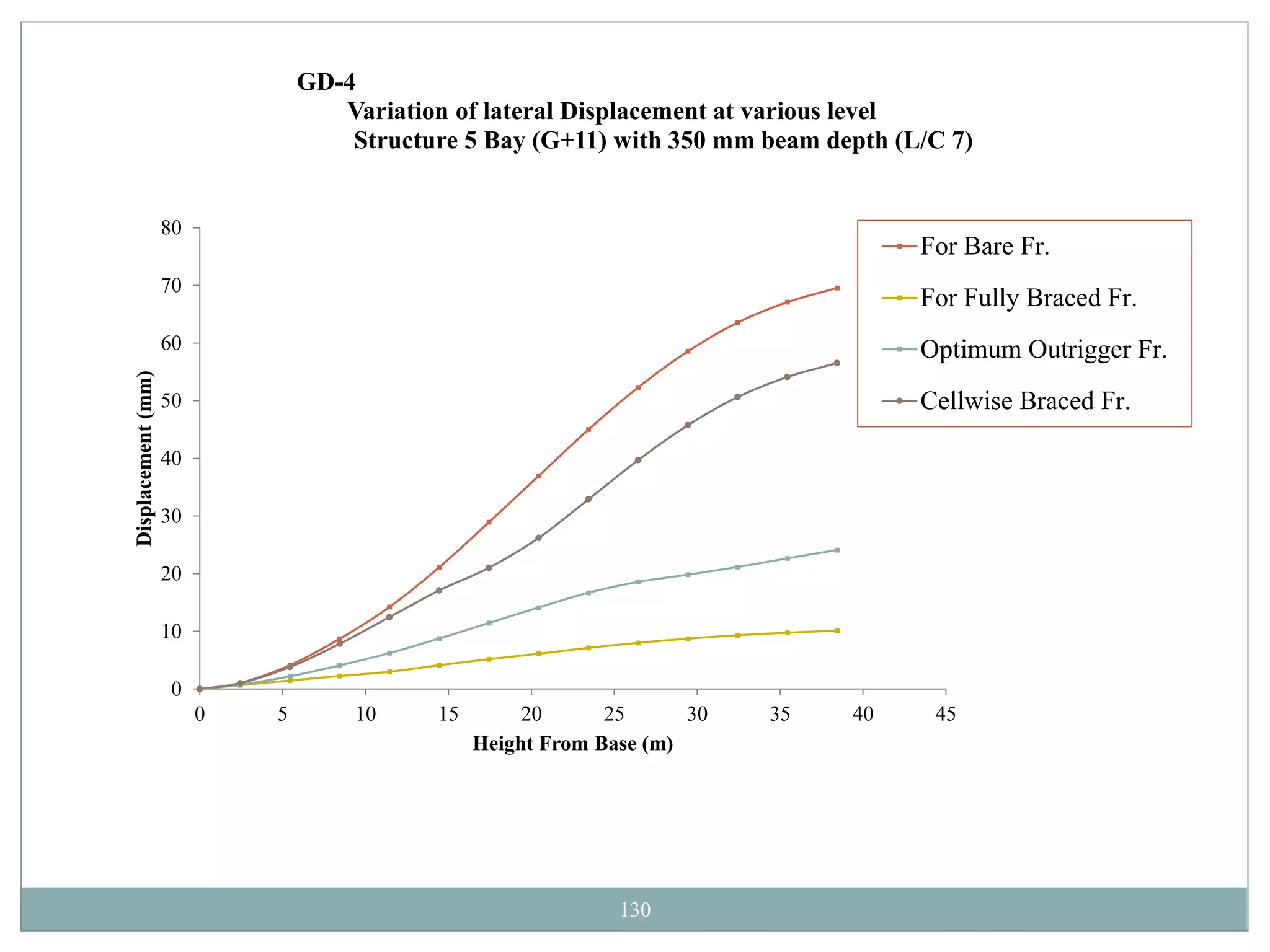
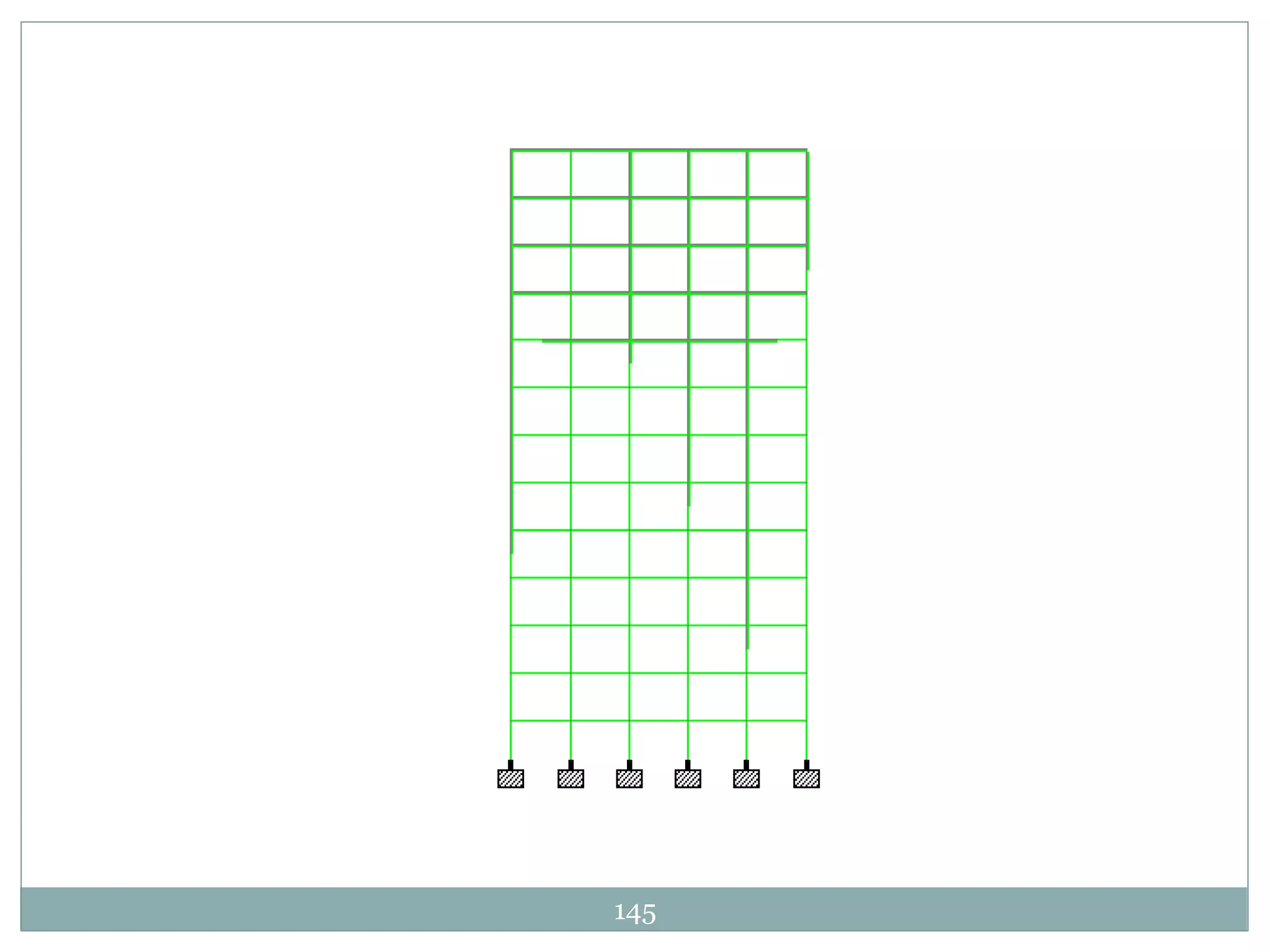
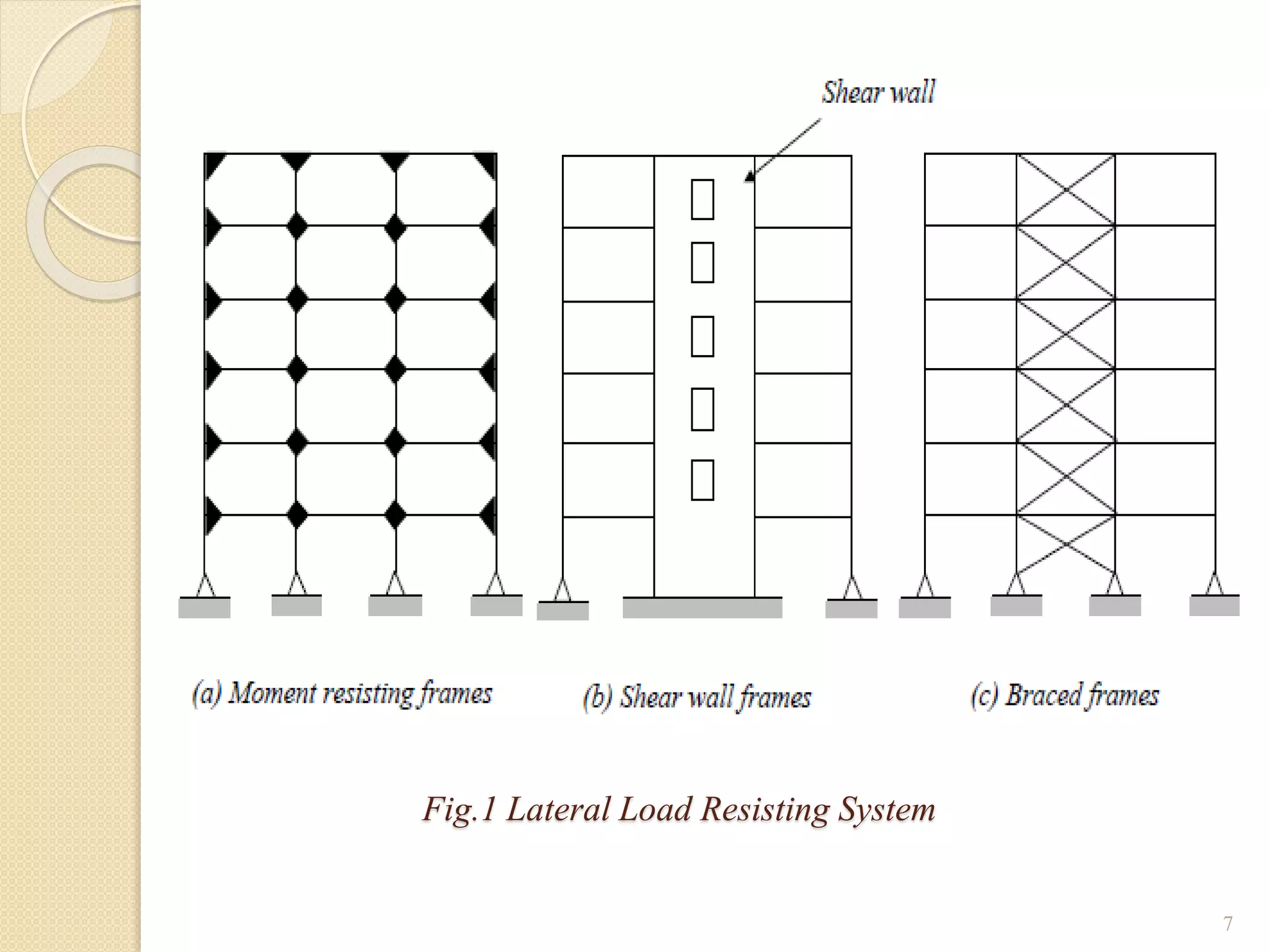
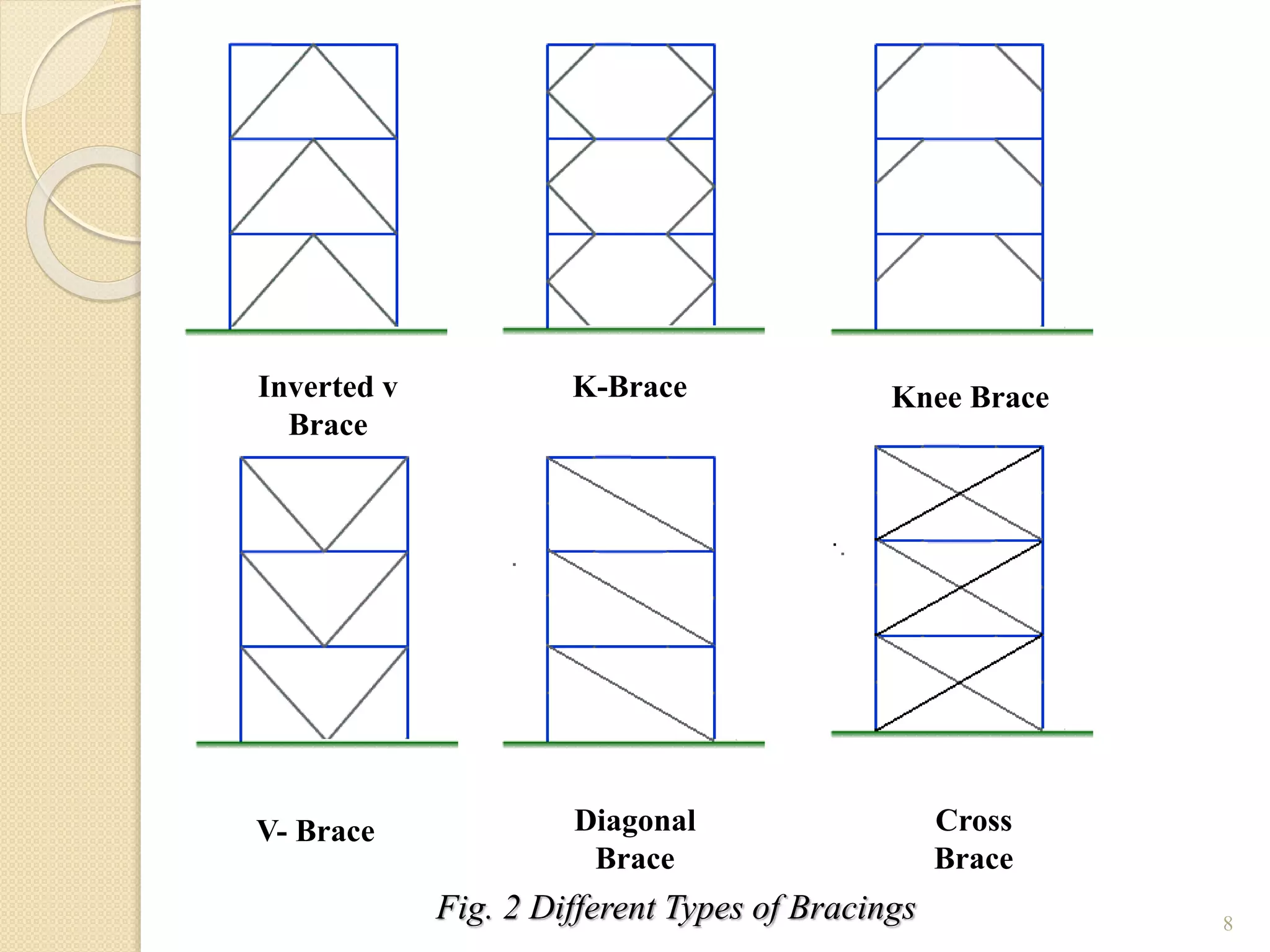
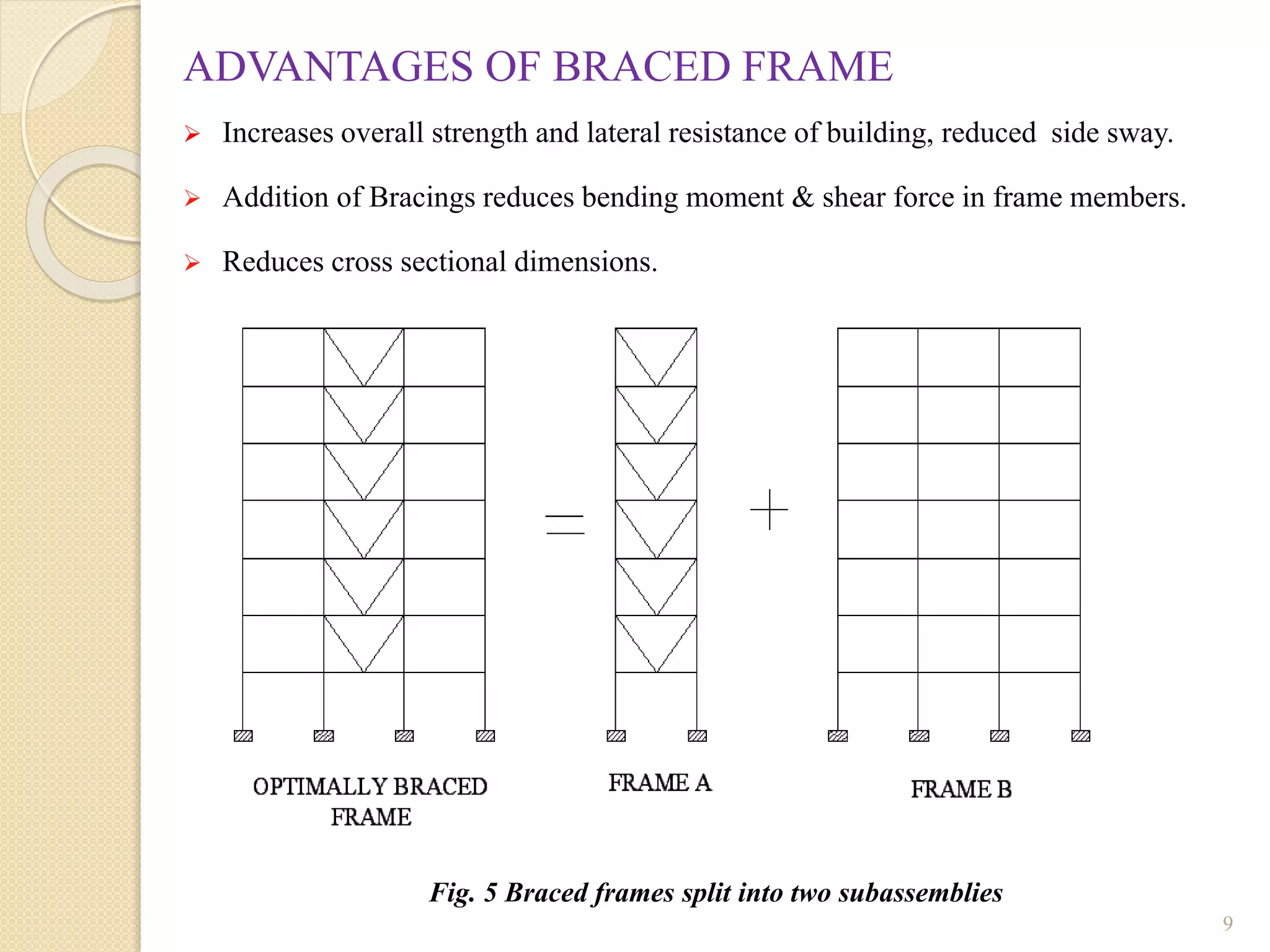
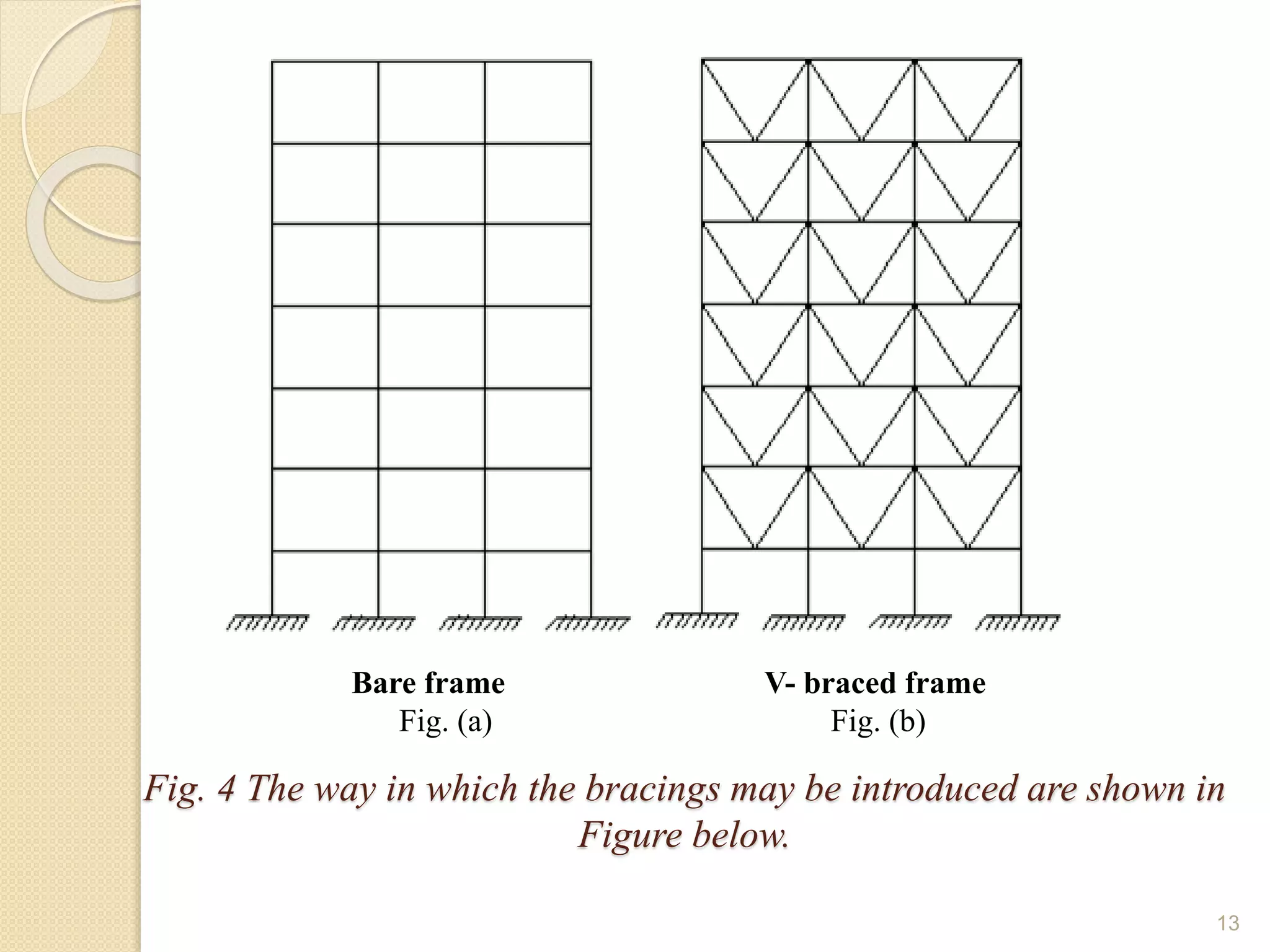
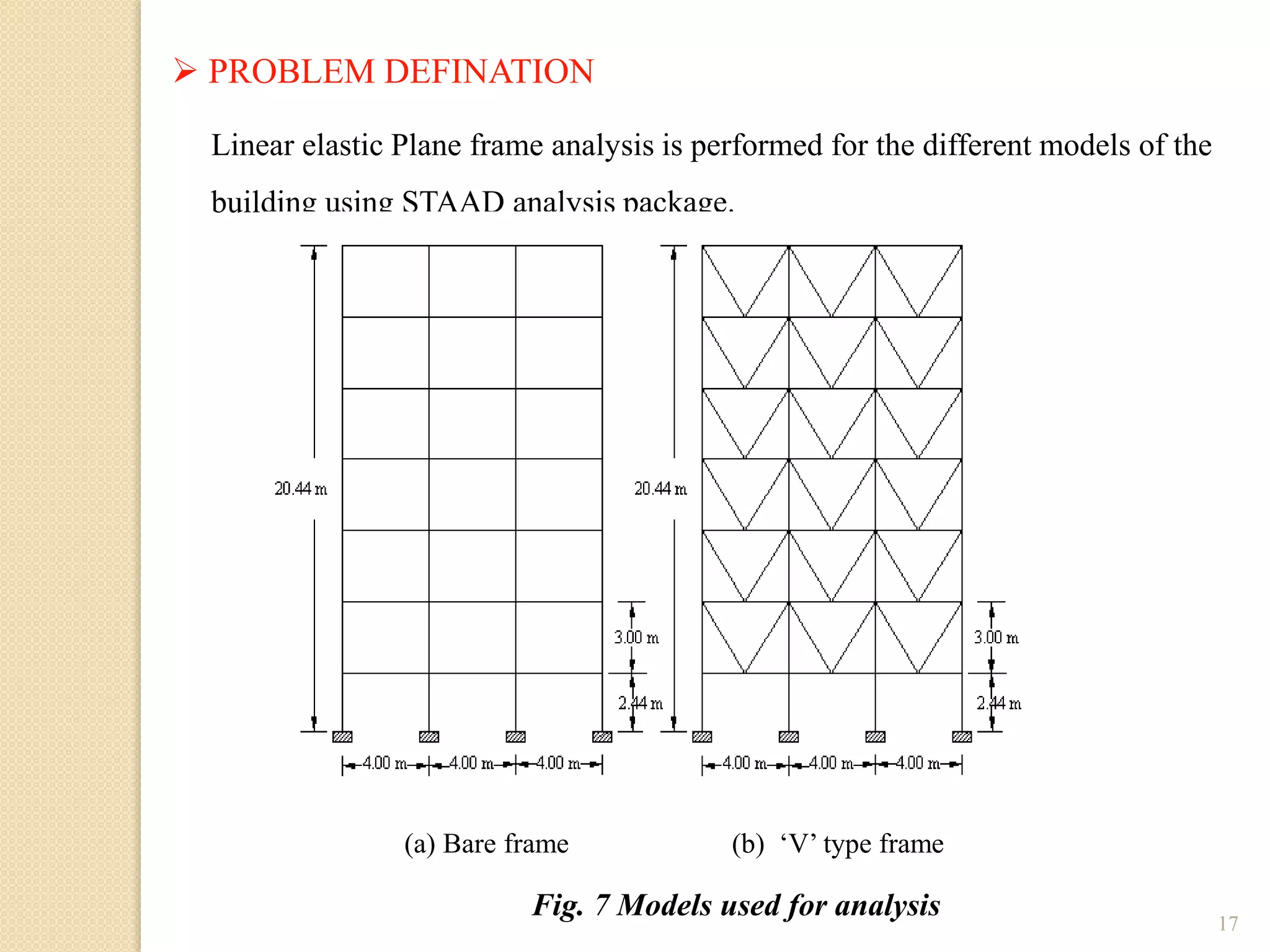
Dissertation report

Presented by
KORE P. N.
Guide
SHRI J.G. KULKARNI
1
A
DISSERTATION REPORT
ON
“ANALYSIS OF MULTISTOREYED PARTIALLY BRACED FRAMES
SUBJECTED TO SEISMIC AND GRAVITY LOADS USING
V – BRACES”

“ANALYSIS OF MULTISTOREYED PARTIALLY BRACED FRAMES
SUBJECTED TO SEISMIC AND GRAVITY LOADING USING
V- BRACES ”
LAYOUT OF PRESENTATION
 INTRODUCTION
 LITERATURE REVIEW
 METHODS OF STRUCTURAL ANALYSIS
 METHODS OF EARTHQUAKE ANALYSIS
 THEORETICAL FORMULATION
 RESULTS AND DISCUSSION
 CONCLUSION
 REFERANCE
2

Importance of Multistoried (tall) Structures:
 Tall structures have fascinated mankind from the beginning of civilisation.
 Tallness of a building is relative and cannot be defined in absolute terms.
 But, from a structural engineer's view point the tall building or multi-storeyed
buildings are one by virtue of its height the lateral forces play an important role in
the structural design.
 The development of the high-rise building has followed the growth of the city
closely.
 Industrialisation causes migration of people to urban centres.
 The land available for buildings to accommodate this migration is becoming scarce,
resulting in rapid increase in the cost of land.
 Thus, developers have looked to the sky.
 Such structures provide a large floor area in a relatively small area of land in urban
centres.
4

 A multi-storey building must resist the combined effects of horizontal &
vertical loads.
 Such structures are more susceptible to earthquake and wind forces, which
may be disastrous in nature.
 To make such structures more stronger & stiffer the cross sections of the
members increases from top to bottom which makes uneconomical
structure.
 Braced frames develop their resistance to lateral forces by the bracing
action of diagonal members.
 Fully braced frames are more rigid.
 From economy point of view arbitrarily braced ones have least forces
induced in the structure.
 At the same time produce maximum displacement within prescribed limits.
5

6
The way in which the bracings may be introduced is shown in Figure above

Fig.1 Lateral Load Resisting System
7

8
Inverted v
Brace
K-Brace Knee Brace
V- Brace Diagonal
Brace
Cross
Brace
Fig. 2 Different Types of Bracings

ADVANTAGES OF BRACED FRAME
 Increases overall strength and lateral resistance of building, reduced side sway.
 Addition of Bracings reduces bending moment & shear force in frame members.
 Reduces cross sectional dimensions.
9
Fig. 5 Braced frames split into two subassemblies

AIM OF WORK
1. The response of bare frames with that of fully braced frames subjected to
gravity as well as lateral loading (i.e. for earthquake forces) have been tried.
2. Few cases have been tried to decide optimum location of braces considering
specific bays as fully braced.
3. Few cases have been tried to decide optimum location of braces considering
specific levels as fully braced.
4. Partially braced frames having combination of (2) and (3) above also have
been analyzed to study and compare the response of such frames.
5. It is also have been tried to locate single cell which being braced yields
maximum economy.
10

Fig. 3 Plan of the building
12

13
Bare frame
Fig. (a)
V- braced frame
Fig. (b)
Fig. 4 The way in which the bracings may be introduced are shown in
Figure below.

 A. R. Khaloo & M. Mahdi Mohseni (1987) had worked on nonlinear seismic
behaviour of RC Frames with RC Braces.
 Kore (2006) worked on single braced (diagonal bracing) and double braced
(cross braced frames) and compared their responses using various
parameters.
 J. P. Desai, A. K. Jain & A. S. Arya (2008) had worked on seismic response
of R.C. Braced Frames with concrete bracing members.
 Pawar (2008) analysed frames with ‘A’ and ‘V’ braces in a similar way.
 Rajput et al (2008) analysed multistoreyed building frames subjected to
gravity and seismic loads considering beams of varying inertia.
 Boga (2009) worked on ‘V’ braced frames with beams of changing stiffness.
 Chopde (2009) worked on ‘V’ braced frames with haunched joints.
14
 Work on concrete bracing

METHODS OF STRUCTUREALANALYSIS
 Slope deflection method.
 Iterative methods like
Moment distribution method (By Hardy Cross in 1930’s)
Kani’s method (by Gasper Kani in 1940’s)
 Approximate methods like
Portal method
Cantilever method
Factor method
 Flexibility coefficient method.
 Stiffness method.
16

17
 PROBLEM DEFINATION
Linear elastic Plane frame analysis is performed for the different models of the
building using STAAD analysis package.
(a) Bare frame (b) ‘V’ type frame
Fig. 7 Models used for analysis

18
(a) Local co-ordinate system (b) Global co-ordinate system
Fig. 6 Plane Frame member
Displacement transformation matrix
Transformation from local to global co-ordinate system

19
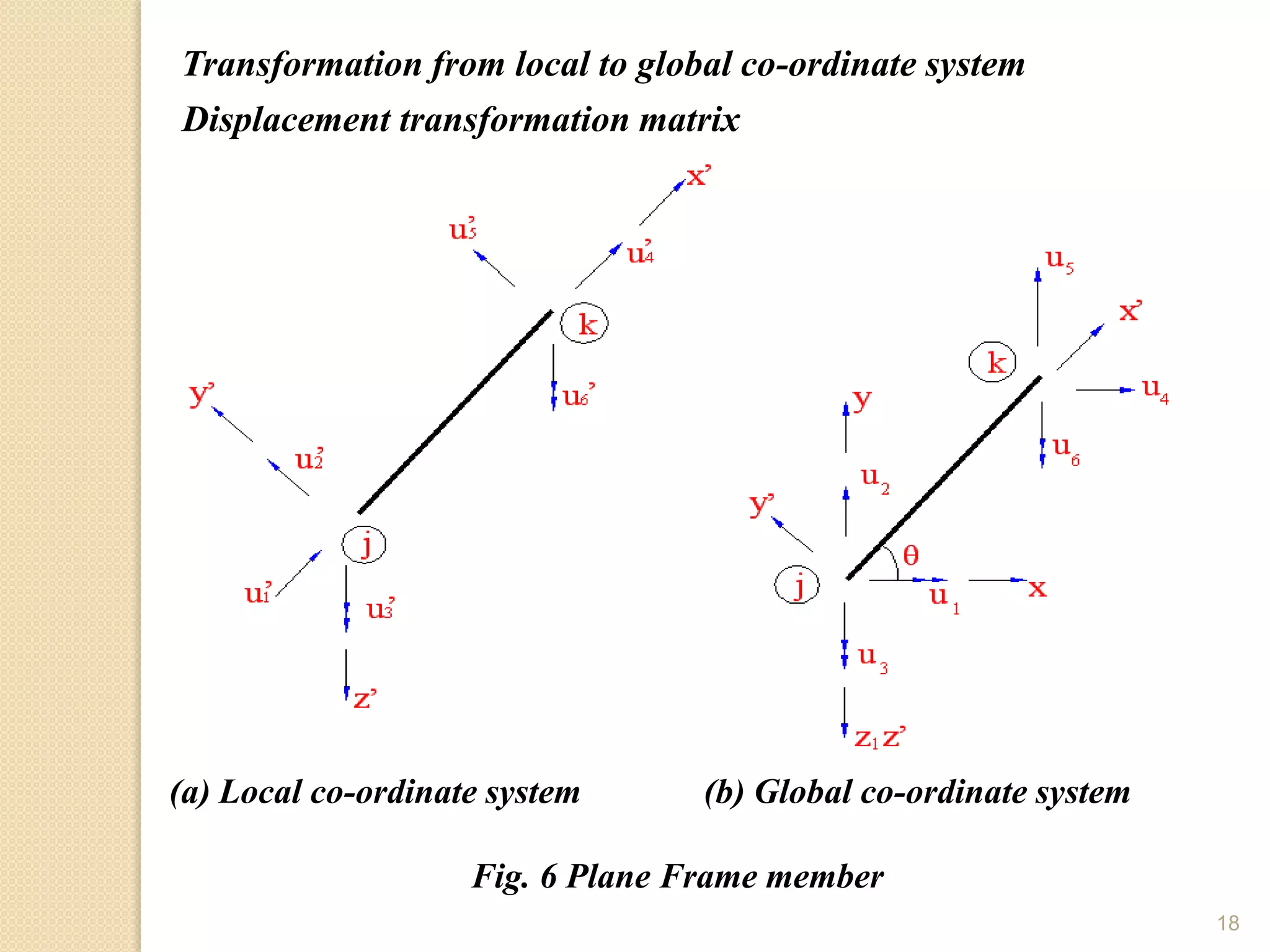
Let θ be the angle by which the member is inclined to global x-axis. From Fig. 6
a and b, one could relate u’1, u’2, u’3 to u1, u2, u3 as,
u’1 = u1 cosθ + u2 sinθ
u’2 = - u1 cosθ + u2 cosθ
u’3 = u3
This may be written as,
Where, l=cosθ and m=sinθ.
This may be written in compact form as,
{u’} = [T] {u} -----(1)

20
Member global stiffness matrix
From above equation, we have
{q’} = [k’] {u’} -----(2)
Substituting the above value of { q’}
{p} = [T] T [k’] {u’}
{p} = [T] T [k’] [T] {u}
{p} = [k] {u}
{k} = [T] T [k] [T] ----(3)
The above equation represents global member stiffness matrix

METHODS OF EARTHQUAKE ANALYSIS
 Approximate Fundamental Period
 Response Spectrum Method
 Modal System
 Equivalent Static Analysis for Evaluation of Lateral Loads as per
Is-1893 (part-I): 2002
21

22
EQUIVALENT STATIC ANALYSIS FOR EVALUATION OF
LATERAL LOADS AS PER IS-1893 (PART-I): 2002
The total design lateral force (design seismic base shear) along any principal
direction shall be calculated by using following expression
VB = Ah W
VB = design seismic base shear
Ah = design horizontal seismic coefficient for structures
W = seismic weight of building
Calculation of design horizontal seismic coefficient (Ah)

23
Z = zone factor
Where,
Im = Importance factor
R = Response reduction factor
Sa/g = average response acceleration coefficient
Distribution of Seismic Forces
Where,
Qi = Design lateral force at floor i,
Wi = Seismic weight of floor i,
hi = Height of floor i measured from base, and
n = Number of storey in the building, the number of levels at which the masses
are located

24
LOAD COMBINATION
In the limit state design of reinforced concrete structures, following load
combinations shall be accounted as per I.S. 1893 (Part I) – 2002. Where the
terms D.L., I.L., and E.L. stand for the response quantities due to dead load,
imposed load and designated earthquake load respectively.
Combinations for limit state
of collapse
Combinations for limit state of
serviceability
1) 1.5 ( DL + LL )
2) 1.2 ( DL + LL ± EQ )
3) 1.5 ( DL ± EQ )
4) 0.9 DL ± 1.5 EQ
1) (DL + 0.8 LL + 0.8 EQ)
2) (DL + LL)
3) (DL + EQ)

25
Column sizes adopted for various floors of G+ 5, G+8 & G+11
Structures For various numbers of bays
Structure Floor level
Bays
3 Bay 5 Bay 7 Bay
G+5
Up to 3rd
300 x 950 300 x 950 300 x 950
3rd
to Terrace 300 x 550 300 x 550 300 x 550
G+8
Up to 3rd 300 x 1150 300 x 1150 300 x 1200
3rd to 6th 300 x 600 300 x 600 300 x 600
6th to Terrace 300 x 550 300 x 550 300 x 550
G+11
Up to 3rd
350 x 1200 350 x 1200 350 x 1200
3rd
to 6th
300 x 750 300 x 750 300 x 750
6th
to 9th
300 x 600 300 x 600 300 x 600
9th
to Terrace 300 x 550 300 x 600 300 x 550

26
PARAMETRIC STUDY
All above frame were analysed to study their response as revealed by the
variation in the following parameters chosen
Internal forces
Optimum bay location for bracings
Optimum level location for bracings
Saving in material cost as compared with bare frame

27
Bare Frames
Frames with ‘V’ Bracing
Frames with Baywise Bracing
Frames with Levelwise Bracing
Frames with Combinations of both i.e. Baywise and Levelwise Bracing
In order to study response of multistoreyed building frame with different geometric
parameters subjected to various types of loads & loading combinations using
different types of bracing patterns following approach was used & following types
of structures were analysed.

28
Total Number of cases for Baywise braced Frames for G+11 Structure
No. of Bays Braced at a time
One Two Three Four Five Six Total
No. of Bays in the Frame
3-bay 3 3 -- -- -- -- 6
5-bay 5 10 10 5 -- -- 30
7-bay 7 21 35 35 21 7 126
Total No. of Cases 162
Total Number of cases for Levelwise braced Frames in a 5 bay structure
No. of Levels Braced at a time
One Two Three Four Five Total
No. of storeys
6 6 15 20 15 6 62
9 9 36 84 -- -- 129
12 12 66 220 -- -- 298
Total number of Combinations 489
Number of cases tried for Baywise and Levelwise Braced Frames:
The total number of baywise and levelwise braced frames analysed: 651

29
OPTIMUM BAYWISE AND LEVELWISE BRACINGS:
Fully braced frame which offers good results as compared to other structural
systems, they pose
Obstacles to free horizontal movements in the structure.
Does not give room for openings such as doors and windows.
and are very conservative in so far as lateral drift is produced concerned
In baywise bracing only particular bay braced or combination of number of
bays which is less than total numbers of bays for the frame and in levelwise
bracing only particular level braced or combination of number of levels
throughout were tried. To find optimum bay location, all combinations of a
number of bays fully braced for G+11 structures with 3 bay, 5 bay and 7 bay
were taken, and for optimum level location few combinations i.e. one level,
two level and three level combinations of a numbers of levels fully braced
throughout for G+5, G+8 and G+11 structure with 5 Bay were taken in to
account.

30
The graphs were prepared indicating the variations of axial force, shear force
and bending moment for various combinations of bracing with different loading
cases. Natural logarithm of reference number ‘N’ as dimensionless parameter
has been used as abscissa with respect to considered parameters. Reference
numbers are obtained using check digit algorithms.
CHECK DIGIT ALGORITHMS:
TYPES OF CHECK DIGIT ALGORITHMS:
Binary algorithms
Weighted algorithms
Special algorithms
Check digit algorithms are used in conventional and bar code numbering to
increase read or scan reliability. This eliminates well over 99% of errors. In
applications requiring very high data integrity a check digit is recommended. A
check digit is derived mathematically from the data content of a character field,
usually a numeric field.

31
Special algorithms are used for alpha and/or alphanumeric character fields.
Each Character is assigned a numeric equivalent. The numeric equivalents are
weighted and the products are summed. The total is divided by the modulus to
determine the remainder. The remainder is compared to a preassigned index to
determine the check digit.
In this project to find out Natural logarithm of reference number for various
optimized frames check digit method were used. The simple example is
elaborated below for 3-bay, bay wise optimization.
Sr.
No.
Bay Weighted Modulus
Remainder
Check
digit
Ref. No. Ln1
(C1)
2
(C2)
3
(C3)
Digit Number
1 0 0 1 2 3 2 1 11 2.397895
2 0 0 2 4 3 1 2 22 3.091042
3 0 0 3 6 3 0 0 30 3.401197
4 0 1 2 7 3 1 2 122 4.804021
5 0 1 3 9 3 0 0 130 4.867534
6 0 2 3 12 3 0 0 230 5.438079
Special algorithms

32
i) 3-bay ii) 5-bay iii) 7-bay
(G+1) (G+11) (G+11)
(a) Frames used for Baywise optimization showing specific member i.e.
‘C1’ used for analysis

33
(b) Frames used for Levelwise optimization showing specific member i.e.
‘C1’ used for analysis.
Fig. 8 The specific member considered for the analysis of various frames with
typical pattern

34
Sr. No. Combination Cases
1 One bay braced at a time 03
2 Two bays braced at a time 03
Total 06
(A) Baywise optimization of 3-bay, (G+11) structure
For baywise analysis of structures, decided combinations are given below, which
have been tried for 3-bay, (G+11) structure for 350 mm beam depth. Following
Table shows the various arrangements of bracing bays for a 3 bay (G+11)
structure.

35
Bracing Arrangement
Various Bay Bracing Arrangement
ln (N)
Case
No.1 2 3
One Bay Braced at a
time
1 √ 2.39790 1
2 √ 3.09104 2
3 √ 3.40120 3
Two Bays Braced at a
time
1+2 √ √ 4.80402 4
1+3 √ √ 4.86753 5
2+3 √ √ 5.43808 6
Table A Various arrangements of bracing bays for a 3 bay (G+11) structure

36
1 Bay Braced 2 Bay Braced
ln (N)
Bare Fr. Braced Fr.
ln (N) Ra ln (N) Ra Ra Ra
2.39790 0.95212 4.80402 0.93595 2.39790 1.00000 1.14221
3.09104 0.94755 4.86753 1.19255 3.09104 1.00000 1.14221
3.40120 1.22078 5.43808 1.13620 3.40120 1.00000 1.14221
4.80402 1.00000 1.14221
4.86753 1.00000 1.14221
5.43808 1.00000 1.14221
TB- 01 Variation of Axial force in member-04 in partially braced frames.
0.90
0.95
1.00
1.05
1.10
1.15
1.20
1.25
2.00 3.00 4.00 5.00 6.00
Ra
ln (N)
GB 01
Variation of Ra for all cases of Bays Braced for 3 bay (G+11) structure
(Mem. No. 4, L/C No. 7) Bottom node
One Bay Braced
Two Bay Braced
Bare Fr.
All Bay Braced Fr.

37
ln (N)
Bare Fr. Braced Fr.
ln (N) Rs ln (N) Rs Rs Rs
2.39790 0.76093 4.80402 0.75437 2.39790 1.00000 1.04871
3.09104 0.88221 4.86753 1.13025 3.09104 1.00000 1.04871
3.40120 1.35085 5.43808 1.17035 3.40120 1.00000 1.04871
4.80402 1.00000 1.04871
4.86753 1.00000 1.04871
5.43808 1.00000 1.04871
TB- 02 Variation of Shear force in member-04 in partially braced frames.
0.70
0.80
0.90
1.00
1.10
1.20
1.30
1.40
2.00 3.00 4.00 5.00 6.00
Rs
ln (N)
GB 02
Variation of Rs for all cases of Bays Braced for 3 bay (G+11) structure
One Bay Braced
Two Bay Braced
Bare Fr.
All Bay Braced Fr.

38
ln (N)
Bare Fr. Braced Fr.
ln (N) Rm ln (N) Rm Rm Rm
2.39790 0.51372 4.80402 0.34927 2.39790 1.00000 0.31284
3.09104 0.47179 4.86753 0.41860 3.09104 1.00000 0.31284
3.40120 0.52153 5.43808 0.35344 3.40120 1.00000 0.31284
4.80402 1.00000 0.31284
4.86753 1.00000 0.31284
5.43808 1.00000 0.31284
TB- 03 Variation of Bending moment in member-04 in partially braced frames.
0.20
0.30
0.40
0.50
0.60
0.70
0.80
0.90
1.00
1.10
2.00 3.00 4.00 5.00 6.00
Rm
ln (N)
GB 03
Variation of Rm for all cases of Bays Braced for 3 bay (G+11) structure
One Bay Braced
Two Bay Braced
Bare Fr.
All Bay Braced Fr.

39
Table B. Various Bay bracing arrangement for 5-bay (G+11) structure.
Bracing
Arrangement
ln (N)
Case
No.1 2 3 4 5
One Bay Braced
1 √ 2.5649 1
2 √ 3.0445 2
3 √ 3.5264 3
4 √ 3.7377 4
5 √ 3.9120 5
Two Bay Braced
1+2 √ √ 4.8122 6
1+3 √ √ 4.8752 7
1+4 √ √ 4.9698 8
1+5 √ √ 5.0239 9
2+3 √ √ 5.4510 10
2+4 √ √ 5.4848 11
2+5 √ √ 5.5373 12
3+4 √ √ 5.8377 13
3+5 √ √ 5.8608 14
4+5 √ √ 6.1159 15
(B) Baywise optimization of 5-bay, (G+11) structure

40
Three Bay Braced
1+2+3 √ √ √ 7.1180 16
1+2+4 √ √ √ 7.1245 17
1+2+5 √ √ √ 7.1309 18
1+3+4 √ √ √ 7.2034 19
1+3+5 √ √ √ 7.2093 20
1+4+5 √ √ √ 7.2821 21
2+3+4 √ √ √ 7.7579 22
2+3+5 √ √ √ 7.7634 23
2+4+5 √ √ √ 7.8038 24
3+4+5 √ √ √ 8.1464 25
Four Bay Braced
1+2+3+4 √ √ √ √ 9.4206 26
1+2+3+5 √ √ √ √ 9.4217 27
1+2+4+5 √ √ √ √ 9.4295 28
1+3+4+5 √ √ √ √ 9.5068 29
2+3+4+5 √ √ √ √ 10.0627 30
Bracing
Arrangement
ln (N)
Case
No.1 2 3 4 5

41
1 Bay Braced 2 Bay Braced 3 Bay Braced 4 Bay Braced
ln (N)
Bare
Fr.
Braced
Fr.
ln (N) Ra ln (N) Ra ln (N) Ra ln (N) Ra Ra Ra
2.5649 0.9624 4.8122 0.9324 7.1180 0.9190 9.4206 0.9242 2.5649 1.0000 1.1545
3.0445 0.9468 4.8752 0.9394 7.1245 0.9373 9.4217 1.1357 3.0445 1.0000 1.1545
3.5264 0.9468 4.9698 0.9569 7.1309 1.1864 9.4295 1.2001 3.5264 1.0000 1.1545
3.7377 0.9658 5.0239 1.2691 7.2034 0.9374 9.5068 1.1815 3.7377 1.0000 1.1545
3.9120 1.3270 5.4510 0.9221 7.2093 1.2008 10.0627 1.1350 3.9120 1.0000 1.1545
5.4848 0.9434 7.2821 1.2353 4.8122 1.0000 1.1545
5.5373 1.2179 7.7579 0.9232 4.8752 1.0000 1.1545
5.8377 0.9367 7.7634 1.1407 4.9698 1.0000 1.1545
5.8608 1.2144 7.8038 1.1857 5.0239 1.0000 1.1545
6.1159 1.2313 8.1464 1.1657 5.4510 1.0000 1.1545
TB- 04 Variation of Axial force in member - 06 in partially braced frames for 5 bay G+11.

42
ln (N)
Bare
Fr.
Braced
Fr.
ln (N) Ra ln (N) Ra ln (N) Ra ln (N) Ra Ra Ra
5.4848 1.0000 1.1545
5.5373 1.0000 1.1545
5.8377 1.0000 1.1545
5.8608 1.0000 1.1545
6.1159 1.0000 1.1545
7.1180 1.0000 1.1545
7.1245 1.0000 1.1545
7.1309 1.0000 1.1545
7.2034 1.0000 1.1545
7.2093 1.0000 1.1545
7.2821 1.0000 1.1545
7.7579 1.0000 1.1545
7.7634 1.0000 1.1545
7.8038 1.0000 1.1545
8.1464 1.0000 1.1545
9.4206 1.0000 1.1545
9.4217 1.0000 1.1545
9.4295 1.0000 1.1545
9.5068 1.0000 1.1545
10.0627 1.0000 1.1545

43
0.80
0.90
1.00
1.10
1.20
1.30
1.40
1 2 3 4 5 6 7 8 9 10 11
Ra
ln (N)
GB 4 Variation of Ra for all cases of Bays Braced for 5 bay (G+11)
One Bay Braced
Two Bay Braced
Three Bay Braced
Four Bay Braced
Bare Fr.
All Bays braced

44
ln (N)
Bare
Fr.
Braced
Fr.
ln (N) Rs ln (N) Rs ln (N) Rs ln (N) Rs Rs Rs
2.5649 0.7289 4.8122 0.6105 7.1180 0.5952 9.4206 0.6794 2.5649 1.0000 1.0611
3.0445 0.7351 4.8752 0.6909 7.1245 0.7116 9.4217 0.9918 3.0445 1.0000 1.0611
3.5264 0.8199 4.9698 0.8439 7.1309 1.0903 9.4295 1.1582 3.5264 1.0000 1.0611
3.7377 1.0286 5.0239 1.3133 7.2034 0.7822 9.5068 1.1942 3.7377 1.0000 1.0611
3.9120 1.6273 5.4510 0.6707 7.2093 1.1653 10.0627 1.1197 3.9120 1.0000 1.0611
5.4848 0.8283 7.2821 1.3240 4.8122 1.0000 1.0611
5.5373 1.2768 7.7579 0.7445 4.8752 1.0000 1.0611
5.8377 0.8757 7.7634 1.0970 4.9698 1.0000 1.0611
5.8608 1.3279 7.8038 1.2697 5.0239 1.0000 1.0611
6.1159 1.4891 8.1464 1.2797 5.4510 1.0000 1.0611
TB- 05 Variation of Shear force in member -06 in partially braced frames for 5 bay G+11.

45
ln (N)
Bare
Fr.
Braced
Fr.
ln (N) Rs ln (N) Rs ln (N) Rs ln (N) Rs Rs Rs
5.4848 1.0000 1.0611
5.5373 1.0000 1.0611
5.8377 1.0000 1.0611
5.8608 1.0000 1.0611
6.1159 1.0000 1.0611
7.1180 1.0000 1.0611
7.1245 1.0000 1.0611
7.1309 1.0000 1.0611
7.2034 1.0000 1.0611
7.2093 1.0000 1.0611
7.2821 1.0000 1.0611
7.7579 1.0000 1.0611
7.7634 1.0000 1.0611
7.8038 1.0000 1.0611
8.1464 1.0000 1.0611
9.4206 1.0000 1.0611
9.4217 1.0000 1.0611
9.4295 1.0000 1.0611
9.5068 1.0000 1.0611
10.0627 1.0000 1.0611

46
0.45
0.65
0.85
1.05
1.25
1.45
1.65
1.85
2 3 4 5 6 7 8 9 10 11
Rs
ln (N)
GB 5 Variation of Rs for all cases of Bays Braced for 5 bay (G+11)
One Bay Braced
Two Bay Braced
Three Bay Braced
Four Bay Braced
Bare Fr.
All Bays braced

47
ln (N)
Bare
Fr.
Braced
Fr.
ln (N) Rm ln (N) Rm ln (N) Rm ln (N) Rm Rm Rm
2.5649 0.5758 4.8122 0.3781 7.1180 0.2974 9.4206 0.2730 2.5649 1.0000 0.3100
3.0445 0.5259 4.8752 0.4272 7.1245 0.3456 9.4217 0.3387 3.0445 1.0000 0.3100
3.5264 0.5448 4.9698 0.4612 7.1309 0.4094 9.4295 0.3711 3.5264 1.0000 0.3100
3.7377 0.5906 5.0239 0.5372 7.2034 0.3519 9.5068 0.3635 3.7377 1.0000 0.3100
3.9120 0.6874 5.4510 0.3558 7.2093 0.4369
10.062
7
0.3251 3.9120 1.0000 0.3100
5.4848 0.4240 7.2821 0.4395 4.8122 1.0000 0.3100
5.5373 0.4956 7.7579 0.3038 4.8752 1.0000 0.3100
5.8377 0.3987 7.7634 0.3793 4.9698 1.0000 0.3100
5.8608 0.5034 7.8038 0.4075 5.0239 1.0000 0.3100
6.1159 0.4957 8.1464 0.3888 5.4510 1.0000 0.3100
TB- 06Variation of Bending Moment in member -06 in partially braced frames for 5 bay G+11

48
ln (N)
Bare
Fr.
Braced
Fr.
ln (N) Rm ln (N) Rm ln (N) Rm ln (N) Rm Rm Rm
5.4848 1.0000 0.3100
5.5373 1.0000 0.3100
5.8377 1.0000 0.3100
5.8608 1.0000 0.3100
6.1159 1.0000 0.3100
7.1180 1.0000 0.3100
7.1245 1.0000 0.3100
7.1309 1.0000 0.3100
7.2034 1.0000 0.3100
7.2093 1.0000 0.3100
7.2821 1.0000 0.3100
7.7579 1.0000 0.3100
7.7634 1.0000 0.3100
7.8038 1.0000 0.3100
8.1464 1.0000 0.3100
9.4206 1.0000 0.3100
9.4217 1.0000 0.3100
9.4295 1.0000 0.3100
9.5068 1.0000 0.3100
10.0627 1.0000 0.3100

49
0.20
0.30
0.40
0.50
0.60
0.70
0.80
0.90
1.00
1.10
2 3 4 5 6 7 8 9 10 11
Rm
ln (N)
GB 6 Variation of Rm for all cases of Bays Braced for 5 bay (G+11)
One Bay Braced
Two Bay Braced
Three Bay Braced
Four Bay Braced
Bare Fr.
All Bays braced

50
C) BAYWISE OPTIMIZATION OF 7-BAY, (G+11) STRUCTURE
For baywise analysis of structures, decided combinations are given below,
which have been tried for 7 bay (G+11) structure. Following Table shows the
various bay bracing arrangement for 5bay (G+11) structure.
1 One bay braced at a time 07
2 Two bays braced at a time 21
3 Three bays braced at a time 35
4 Four bays braced at a time 35
5 Five bays braced at a time 21
6 Six bays braced at a time 07
Total 126

51
Bracing
Arrangement
ln (N)
Case
No.1 2 3 4 5 6 7
1 √ 2.70805 1
2 √ 3.13549 2
3 √ 3.43399 3
One Bay Braced 4 √ 3.82864 4
5 √ 3.98898 5
6 √ 4.12713 6
7 √ 4.24850 7
1+2 √ √ 4.78749 8
1+3 √ √ 4.90527 9
1+4 √ √ 4.96284 10
1+5 √ √ 5.01728 11
1+6 √ √ 5.11199 12
1+7 √ √ 5.15906 13
2+3 √ √ 5.44674 14
Two Bay Braced 2+4 √ √ 5.48064 15
2+5 √ √ 5.54126 16
Table C. Various Bay bracing arrangement for 7-bay (G+11) structure.

52
TB- 07 Variation of axial force in member -08 in partially braced frames for 7 bay G+11.
1 Bay Braced 2 Bay Braced 3 Bay Braced 4 Bay Braced 5 Bay Braced 6 Bay Braced
ln (N)
Bare
Fr.
Braced
Fr.
ln (N) Ra ln (N) Ra ln (N) Ra ln (N) Ra ln (N) Ra ln (N) Ra Ra Ra
2.708 0.969 4.788 0.939 7.119 0.923 9.421 0.915 11.724 0.911 14.026 0.919 2.708 1.000 1.153
3.136 0.955 4.905 0.946 7.125 0.930 9.422 0.920 11.724 0.922 14.026 1.107 3.136 1.000 1.153
3.434 0.954 4.963 0.945 7.132 0.932 9.422 0.931 11.724 1.127 14.026 1.169 3.434 1.000 1.153
3.829 0.954 5.017 0.947 7.144 0.946 9.424 1.165 11.725 0.929 14.027 1.191 3.829 1.000 1.153
3.989 0.956 5.112 0.967 7.150 1.229 9.430 0.922 11.725 1.148 14.035 1.185 3.989 1.000 1.153
4.127 0.978 5.159 1.326 7.200 0.927 9.431 0.938 11.725 1.204 14.112 1.163 4.127 1.000 1.153
4.249 1.400 5.447 0.928 7.212 0.935 9.431 1.191 11.733 0.929 14.668 1.136 4.249 1.000 1.153
5.481 0.937 7.217 0.950 9.438 0.938 11.733 1.152 4.788 1.000 1.153
5.541 0.939 7.223 1.248 9.439 1.195 11.734 1.223 4.905 1.000 1.153

53
0.80
0.90
1.00
1.10
1.20
1.30
1.40
1.50
1.00 3.00 5.00 7.00 9.00 11.00 13.00 15.00
Ra
ln (N)
GB 7 Variation of Ra for all cases of Bays Braced for 7 bay (G+11)
One Bay Braced
Two Bay Braced
Three Bay
Braced
Four Bay Braced
Five Bay Braced
Six Bay Braced

54
ln (N)
Bare Fr.
Braced
Fr.
ln (N) Rs ln (N) Rs ln (N) Rs ln (N) Rs ln (N) Rs ln (N) Rs Rs Rs
2.708 0.736 4.788 0.587 7.119 0.523 9.421 0.507 11.724 0.535 14.026 0.642 2.708 1.000 1.071
3.136 0.719 4.905 0.632 7.125 0.566 9.422 0.553 11.724 0.612 14.026 0.928 3.136 1.000 1.071
3.434 0.747 4.963 0.672 7.132 0.622 9.422 0.656 11.724 0.951 14.026 1.083 3.434 1.000 1.071
3.829 0.799 5.017 0.749 7.144 0.755 9.424 1.035 11.725 0.684 14.027 1.163 3.829 1.000 1.071
3.989 0.903 5.112 0.932 7.150 1.196 9.430 0.597 11.725 1.005 14.035 1.187 3.989 1.000 1.071
4.127 1.148 5.159 1.478 7.200 0.586 9.431 0.702 11.725 1.182 14.112 1.164 4.127 1.000 1.071
4.249 1.839 5.447 0.592 7.212 0.657 9.431 1.095 11.733 0.724 14.668 1.091 4.249 1.000 1.071
5.481 0.653 7.217 0.800 9.438 0.773 11.733 1.048 4.788 1.000 1.071
5.541 0.727 7.223 1.258 9.439 1.138 11.734 1.234 4.905 1.000 1.071
5.572 0.900 7.281 0.680 9.447 1.340 11.741 1.284 4.963 1.000 1.071
5.602 1.427 7.286 0.825 9.507 0.606 11.810 0.720 5.017 1.000 1.071
5.841 0.648 7.296 1.285 9.508 0.713 11.810 1.044 5.112 1.000 1.071
TB- 08 Variation of shear force in member -08 in partially braced frames for 7 bay G+11.

55
0.40
0.60
0.80
1.00
1.20
1.40
1.60
1.80
2.00
1.50 3.50 5.50 7.50 9.50 11.50 13.50 15.50
Rs
ln (N)
GB 8 Variation of Rs for all cases of Bays Braced for 7 bay (G+11)
One Bay Braced
Two Bay Braced
Three Bay Braced
Four Bay Braced
Five Bay Braced
Six Bay Braced
Bare Fr.
All Bay Braced

56
TB- 09 Variation of Bending Moment in member -08 in partially braced frames for 7 bay G+11.
ln (N)
Bare Fr.
Braced
Fr.
ln (N) Rm ln (N) Rm ln (N) Rm ln (N) Rm ln (N) Rm ln (N) Rm Rm Rm
2.708 0.625 4.788 0.413 7.119 0.313 9.421 0.263 11.724 0.242 14.026 0.247 2.708 1.000 0.312
3.136 0.576 4.905 0.460 7.125 0.352 9.422 0.291 11.724 0.268 14.026 0.303 3.136 1.000 0.312
3.434 0.582 4.963 0.469 7.132 0.368 9.422 0.314 11.724 0.331 14.026 0.339 3.434 1.000 0.312
3.829 0.598 5.017 0.493 7.144 0.397 9.424 0.384 11.725 0.292 14.027 0.357 3.829 1.000 0.312
3.989 0.626 5.112 0.534 7.150 0.477 9.430 0.309 11.725 0.356 14.035 0.358 3.989 1.000 0.312
4.127 0.682 5.159 0.632 7.200 0.349 9.431 0.346 11.725 0.385 14.112 0.345 4.127 1.000 0.312
4.249 0.807 5.447 0.381 7.212 0.394 9.431 0.417 11.733 0.301 14.668 0.316 4.249 1.000 0.312
5.481 0.437 7.217 0.427 9.438 0.350 11.733 0.369 4.788 1.000 0.312
5.541 0.458 7.223 0.509 9.439 0.427 11.734 0.406 4.905 1.000 0.312
5.572 0.496 7.281 0.381 9.447 0.453 11.741 0.404 4.963 1.000 0.312
5.602 0.589 7.286 0.431 9.507 0.298 11.810 0.289 5.017 1.000 0.312
5.841 0.396 7.296 0.512 9.508 0.340 11.810 0.356 5.112 1.000 0.312
5.864 0.459 7.355 0.425 9.509 0.410 11.811 0.397 5.159 1.000 0.312

57
0.20
0.30
0.40
0.50
0.60
0.70
0.80
0.90
1.00
1.10
1.50 3.50 5.50 7.50 9.50 11.50 13.50 15.50
Rm
ln (N)
GB 9 Variation of Rm for all cases of Bays Braced for 7 bay (G+11)
One Bay Braced
Two Bay Braced
Three Bay
Braced
Four Bay Braced
Five Bay Braced
Six Bay Braced
Bare Fr.

58
LEVELWISE OPTIMIZATION OF BRACINGS:
(A) LEVELWISE OPTIMIZATION OF 5-BAY, (G+5) STRUCTURE:
For levelwise analysis of structures, decided combinations are given below,
which have been tried for 5bay (G+5) structure. Following Table shows the
various level bracing arrangement for 5bay (G+5) structure.
1 One Level braced at a time 6
2 Two Level braced at a time 15
3 Three Level braced at a time 20
4 Four Level braced at a time 15
5 Five Level braced at a time 6
Sum Total Frames 62

59
Table A. Various Levels bracing arrangement for 5-bay (G+5) structure
Bracing Arrangement
Various Level Bracing Arrangement
ln (N) Case No.
G 1 2 3 4 5
One Level Braced
G √ 3.13549 1
1 √ 3.43399 2
2 √ 3.82864 3
3 √ 3.98898 4
4 √ 4.12713 5
5 √ 4.24850 6
Two Level Braced
G+1 √ √ 5.44674 7
G+2 √ √ 5.48064 8
G+3 √ √ 5.54126 9
G+4 √ √ 5.57215 10
G+5 √ √ 5.60212 11
1+2 √ √ 5.84064 12
1+3 √ √ 5.86363 13
1+4 √ √ 5.88610 14
1+5 √ √ 5.92693 15
2+3 √ √ 6.12249 16
2+4 √ √ 6.13988 17
2+5 √ √ 6.15698 18
3+4 √ √ 6.32972 19
3+5 √ √ 6.35611 20

60
TL- 10 Variation of Axial force in member -04 in partially braced frames for 5 bay G+5.
1 Level Braced 2 Level Braced 3 Level Braced 4 Level Braced 5 Level Braced
ln (N)
Bare Fr.
Braced
Fr.
ln (N) Ra ln (N) Ra ln (N) Ra ln (N) Ra ln (N) Ra Ra Ra
3.136 1.048 5.447 1.065 7.759 1.083 10.063 1.105 12.366 1.122 3.136 1.000 1.130
3.434 1.041 5.481 1.068 7.763 1.085 10.063 1.098 12.366 1.111 3.434 1.000 1.130
3.829 1.034 5.541 1.069 7.769 1.082 10.064 1.091 12.366 1.054 3.829 1.000 1.130
3.989 1.030 5.572 1.069 7.772 1.076 10.067 1.103 12.370 1.114 3.989 1.000 1.130
4.127 1.026 5.602 1.062 7.806 1.088 10.068 1.094 12.412 1.118 4.127 1.000 1.130
4.249 1.017 5.841 1.058 7.809 1.085 10.072 1.094 12.753 1.110 4.249 1.000 1.130
5.864 1.063 7.812 1.078 10.109 1.108 5.447 1.000 1.130
5.886 1.061 7.848 1.089 10.109 1.096 5.481 1.000 1.130
5.927 1.054 7.854 1.080 10.114 1.096 5.541 1.000 1.130
6.123 1.057 7.891 1.082 10.153 1.102 5.572 1.000 1.130
6.140 1.054 8.146 1.081 10.451 1.101 5.602 1.000 1.130
6.157 1.046 8.151 1.075 10.451 1.089 5.841 1.000 1.130
6.330 1.052 8.153 1.068 10.454 1.086 5.864 1.000 1.130
6.356 1.042 8.178 1.083 10.482 1.095 5.886 1.000 1.130
6.512 1.041 8.181 1.073 10.729 1.090 5.927 1.000 1.130
8.209 1.074 6.123 1.000 1.130

61
0.99
1.01
1.03
1.05
1.07
1.09
1.11
1.13
1.15
2.00 3.00 4.00 5.00 6.00 7.00 8.00 9.00 10.00 11.00 12.00 13.00 14.00
Ra
ln (N)
GL 10- Variation of Ra for all cases of levels braced For 5 Bay (G+5),
(Mem. No. 6,L/C No. 7) Bottom node
One Level Braced
Two Level Braced
Three Level
Braced
Four Level Braced
Five Level Braced

62
TL- 11 Variation of Shear force in member -04 in partially braced frames for 5 bay G+5.
ln (N)
Bare Fr.
ln (N) Rs ln (N) Rs ln (N) Rs ln (N) Rs ln (N) Rs Rs
3.136 1.024 5.447 1.165 7.759 1.155 10.063 1.129 12.366 1.104 3.136 1
3.434 1.101 5.481 1.081 7.763 1.134 10.063 1.131 12.366 1.118 3.434 1
3.829 1.027 5.541 1.023 7.769 1.138 10.064 1.14 12.366 1.088 3.829 1
3.989 1.004 5.572 1.006 7.772 1.147 10.067 1.11 12.37 1.095 3.989 1
4.127 1.002 5.602 1.008 7.806 1.054 10.068 1.122 12.412 1.024 4.127 1
4.249 1 5.841 1.088 7.809 1.06 10.072 1.121 12.753 1.069 4.249 1
5.864 1.089 7.812 1.068 10.109 1.034 5.447 1
5.886 1.095 7.848 1.001 10.109 1.045 5.481 1
5.927 1.097 7.854 1.012 10.114 1.048 5.541 1
6.123 1.016 7.891 0.992 10.153 0.99 5.572 1
6.14 1.026 8.146 1.077 10.451 1.071 5.602 1
6.157 1.027 8.151 1.083 10.451 1.075 5.841 1
6.33 1.002 8.153 1.085 10.454 1.08 5.864 1
6.356 1.004 8.178 1.083 10.482 1.079 5.886 1
6.512 1.001 8.181 1.086 10.729 1.016 5.927 1
8.209 1.091 6.123 1
8.426 1.015 6.14 1
8.428 1.017 6.157 1
8.449 1.027 6.33 1
8.644 1.002 6.356 1
6.512 1
7.759 1
7.763 1

63
0.98
1.00
1.02
1.04
1.06
1.08
1.10
1.12
1.14
1.16
1.18
2.00 4.00 6.00 8.00 10.00 12.00 14.00
Rs
ln (N)
GL 11- Variation of Rs for all cases of levels braced For 5 Bay (G+5),
(Mem. No. 6, L/C No. 7) Bottom node One Level Braced
Two Level Braced
Three Level Braced
Four Level Braced
Five Level Braced
Bare Fr.
All Level Braced

64
TL- 12 Variation of Bending Moment in member -04 in partially braced frames.
ln (N)
Bare Fr.
Braced
Fr.
ln (N) Rm ln (N) Rm ln (N) Rm ln (N) Rm ln (N) Rm Rm Rm
3.1355 0.3615 5.4467 0.4057 7.7592 0.4107 10.0628 0.4040 12.3655 0.3958 3.1355 1.0000 0.3909
3.4340 0.6055 5.4806 0.3859 7.7626 0.3992 10.0632 0.4027 12.3655 0.4000 3.4340 1.0000 0.3909
3.8286 0.7556 5.5413 0.3635 7.7690 0.3977 10.0635 0.4058 12.3659 0.3888 3.8286 1.0000 0.3909
3.9890 0.8911 5.5722 0.3577 7.7723 0.4003 10.0673 0.3912 12.3702 0.3865 3.9890 1.0000 0.3909
4.1271 0.9766 5.6021 0.3579 7.8059 0.3789 10.0679 0.3952 12.4117 0.3706 4.1271 1.0000 0.3909
4.2485 0.9953 5.8406 0.6123 7.8091 0.3803 10.0720 0.3926 12.7532 0.6019 4.2485 1.0000 0.3909
5.8636 0.6040 7.8124 0.3823 10.1090 0.3735 5.4467 1.0000 0.3909
5.8861 0.6020 7.8478 0.3578 10.1093 0.3765 5.4806 1.0000 0.3909
5.9269 0.6029 7.8536 0.3610 10.1135 0.3770 5.5413 1.0000 0.3909
6.1225 0.7529 7.8906 0.3546 10.1531 0.3554 5.5722 1.0000 0.3909
6.1399 0.7547 8.1464 0.6086 10.4506 0.6044 5.6021 1.0000 0.3909
6.1570 0.7550 8.1508 0.6082 10.4508 0.6066 5.8406 1.0000 0.3909
6.3297 0.8944 8.1531 0.6098 10.4536 0.6055 5.8636 1.0000 0.3909
6.3561 0.8923 8.1784 0.5998 10.4821 0.5974 5.8861 1.0000 0.3909
6.5117 0.9767 8.1806 0.6019 10.7293 0.7511 5.9269 1.0000 0.3909
8.2093 0.5993 6.1225 1.0000 0.3909
8.4264 0.7515 6.1399 1.0000 0.3909
8.4281 0.7526 6.1570 1.0000 0.3909

65
0.30
0.40
0.50
0.60
0.70
0.80
0.90
1.00
1.10
1.20
1.90 3.90 5.90 7.90 9.90 11.90
Rm
ln (N)
GL 12- Variation of Rm for all cases of levels braced For 5 Bay (G+5),
One Level Braced
Two Level Braced
Three level Braced
Four Level Braced

66
(B) LEVELWISE OPTIMIZATION OF 5-BAY, (G+8) STRUCTURE
Sum Total Frames 129

67
Various Level bracing arrangement for 5- bay (G+8) structure
Bracing Arrangement
ln (N)
Case
No.G 1 2 3 4 5 6 7 8
One Level Braced
G √ 3.25810 1
1 √ 3.52636 2
2 √ 3.73767 3
3 √ 3.91202 4
4 √ 4.21951 5
5 √ 4.33073 6
6 √ 4.43082 7
7 √ 4.52179 8
8 √ 4.60517 9
Two Level Braced
G+1 √ √ 5.47227 10
G+2 √ √ 5.50533 11
G+3 √ √ 5.53733 12
G+4 √ √ 5.56834 13

68
TL- 13 Variation of Axial force in member 04 in partially braced frames
1 Level Braced 2 Level Braced 3 Level Braced
ln (N)
Bare Fr. Braced Fr.
ln (N) Ra ln (N) Ra ln (N) Ra Ra Ra
3.25810 1.04494 5.47227 1.06185 7.76004 1.07720 3.25810 1.00000 1.15357
3.52636 1.04170 5.50533 1.06432 7.76345 1.08221 3.52636 1.00000 1.15357
3.73767 1.03630 5.53733 1.06622 7.76684 1.07997 3.73767 1.00000 1.15357
3.91202 1.03226 5.56834 1.06610 7.77444 1.08066 3.91202 1.00000 1.15357
4.21951 1.02714 5.59842 1.06732 7.77779 1.08178 4.21951 1.00000 1.15357
4.33073 1.02644 5.66296 1.06832 7.78114 1.08168 4.33073 1.00000 1.15357
4.43082 1.02676 5.69036 1.06808 7.78447 1.07653 4.43082 1.00000 1.15357
4.52179 1.02620 5.71703 1.06225 7.80384 1.08403 4.52179 1.00000 1.15357
4.60517 1.01978 5.83773 1.05682 7.81116 1.08337 4.60517 1.00000 1.15357
5.86079 1.06361 7.81440 1.08205 5.47227 1.00000 1.15357
5.91080 1.06214 7.81763 1.08306 5.50533 1.00000 1.15357
5.93225 1.06268 7.82084 1.08309 5.53733 1.00000 1.15357
5.95324 1.06378 7.82405 1.07813 5.56834 1.00000 1.15357
5.97381 1.06363 7.84971 1.08548 5.59842 1.00000 1.15357

69
0.98
1.00
1.02
1.04
1.06
1.08
1.10
1.12
1.14
1.16
3.00 4.00 5.00 6.00 7.00 8.00 9.00
Ra
ln (N)
GL 13- Variation of Ra for all cases of levels bracedFor 5 Bay (G+8),
Two Level Braced
Three Level Braced
Bare Fr.
Three Level Braced Com.

70
Variation of Shear force in member -04 in partially braced frames.
ln (N)
Bare Fr. Braced Fr.
ln (N) Rs ln (N) Rs ln (N) Rs Rs Rs
3.25810 0.98198 5.47227 1.20394 7.76004 1.22877 3.25810 1.00000 1.07884
3.52636 1.12704 5.50533 1.11668 7.76345 1.17658 3.52636 1.00000 1.07884
3.73767 1.05187 5.53733 1.00758 7.76684 1.16592 3.73767 1.00000 1.07884
3.91202 0.99534 5.56834 0.96758 7.77444 1.16666 3.91202 1.00000 1.07884
4.21951 0.99938 5.59842 0.95857 7.77779 1.16468 4.21951 1.00000 1.07884
4.33073 1.00086 5.66296 0.95239 7.78114 1.16488 4.33073 1.00000 1.07884
4.43082 0.99890 5.69036 0.95123 7.78447 1.17409 4.43082 1.00000 1.07884
4.52179 0.99837 5.71703 0.95760 7.80384 1.08233 4.52179 1.00000 1.07884
4.60517 0.99866 5.83773 1.13484 7.81116 1.08503 4.60517 1.00000 1.07884
5.86079 1.10736 7.81440 1.08917 5.47227 1.00000 1.07884
5.91080 1.11268 7.81763 1.08798 5.50533 1.00000 1.07884
5.93225 1.11457 7.82084 1.08816 5.53733 1.00000 1.07884
5.95324 1.11372 7.82405 1.09486 5.56834 1.00000 1.07884
5.97381 1.11376 7.84971 0.97167 5.59842 1.00000 1.07884
5.99396 1.11699 7.85283 0.98319 5.66296 1.00000 1.07884
6.12687 1.02547 7.85593 0.98712 5.69036 1.00000 1.07884
6.14419 1.04455 7.86288 0.98767 5.71703 1.00000 1.07884
6.16121 1.05059 7.86596 0.99251 5.83773 1.00000 1.07884

71
0.90
0.95
1.00
1.05
1.10
1.15
1.20
1.25
3.00 4.00 5.00 6.00 7.00 8.00 9.00
Rs
ln (N)
GL 14- Variation of Rs for all cases of levels braced For 5 Bay (G+8),
One Level Braced
Two Level Braced
Three Level Braced
Bare Fr.

72
Variation of Bending moment in member -04 in partially braced frames.
ln (N)
Bare Fr. Braced Fr.
ln (N) Rm ln (N) Rm ln (N) Rm Rm Rm
3.2581 0.3462 5.4723 0.3547 7.7600 0.3701 3.2581 1.0000 0.3338
3.5264 0.5330 5.5053 0.3542 7.7634 0.3530 3.5264 1.0000 0.3338
3.7377 0.6641 5.5373 0.3372 7.7668 0.3458 3.7377 1.0000 0.3338
3.9120 0.8108 5.5683 0.3380 7.7744 0.3461 3.9120 1.0000 0.3338
4.2195 0.9400 5.5984 0.3409 7.7778 0.3456 4.2195 1.0000 0.3338
4.3307 0.9809 5.6630 0.3410 7.7811 0.3456 4.3307 1.0000 0.3338
4.4308 0.9940 5.6904 0.3411 7.7845 0.3477 4.4308 1.0000 0.3338
4.5218 0.9981 5.7170 0.3422 7.8038 0.3487 4.5218 1.0000 0.3338
4.6052 0.9992 5.8377 0.5321 7.8112 0.3471 4.6052 1.0000 0.3338
5.8608 0.5233 7.8144 0.3480 5.4723 1.0000 0.3338
5.9108 0.5241 7.8176 0.3478 5.5053 1.0000 0.3338
5.9322 0.5266 7.8208 0.3479 5.5373 1.0000 0.3338
5.9532 0.5270 7.8240 0.3493 5.5683 1.0000 0.3338
5.9738 0.5272 7.8497 0.3306 5.5984 1.0000 0.3338
5.9940 0.5286 7.8528 0.3336 5.6630 1.0000 0.3338
6.1269 0.6528 7.8559 0.3341 5.6904 1.0000 0.3338
6.1442 0.6579 7.8629 0.3340 5.7170 1.0000 0.3338
6.1612 0.6607 7.8660 0.3347 5.8377 1.0000 0.3338
6.1779 0.6612 7.8898 0.3342 5.8608 1.0000 0.3338
6.1944 0.6615 7.8966 0.3348 5.9108 1.0000 0.3338
6.2305 0.6621 7.8995 0.3353 5.9322 1.0000 0.3338

73
0.25
0.35
0.45
0.55
0.65
0.75
0.85
0.95
1.05
3.00 4.00 5.00 6.00 7.00 8.00 9.00
Rm
ln (N)
GL 15- Variation of Rm for all cases of levels braced For 5 Bay (G+8),
One Level Braced
Two Level Braced
Three Level Braced
Bare Fr.

74
(C) LEVELWISE OPTIMIZATION OF 5-BAY, (G+11) STRUCTURE:
Total 298

75
Various Levels bracing arrangement for 5- bay (G+11) structure
Bracing
Arrangement
ln (N)
Case
No.G 1 2 3 4 5 6 7 8 9 10 11
One Level Braced G √ 3.43399 1
1 √ 3.66356 2
2 √ 3.85015 3
3 √ 4.00733 4
4 √ 4.14313 5
5 √ 4.26268 6
6 √ 4.52179 7
7 √ 4.60517 8
8 √ 4.68213 9
9 √ 4.75359 10
10 √ 4.82028 11
11 √ 4.88280 12
Two Level Braced G+1 √ √ 5.45104 13
G+2 √ √ 5.48480 14
G+3 √ √ 5.56834 15
G+4 √ √ 5.59842 16

76
Variation of Axial force in member 04 in partially braced frames
ln (N)
Bare Fr. Braced Fr.
ln (N) Ra ln (N) Ra ln (N) Ra Ra Ra
3.4340 1.0388 5.4510 1.0539 7.7592 1.0674 3.4340 1.0000 1.1545
3.6636 1.0372 5.4848 1.0566 7.7626 1.0726 3.6636 1.0000 1.1545
3.8501 1.0338 5.5683 1.0588 7.7715 1.0716 3.8501 1.0000 1.1545
4.0073 1.0313 5.5984 1.0589 7.7749 1.0717 4.0073 1.0000 1.1545
4.1431 1.0268 5.6276 1.0596 7.7782 1.0733 4.1431 1.0000 1.1545
4.2627 1.0252 5.6560 1.0611 7.7816 1.0738 4.2627 1.0000 1.1545
4.5218 1.0255 5.6836 1.0614 7.7849 1.0744 4.5218 1.0000 1.1545
4.6052 1.0251 5.7104 1.0620 7.7882 1.0747 4.6052 1.0000 1.1545
4.6821 1.0255 5.7366 1.0622 7.7915 1.0745 4.6821 1.0000 1.1545
4.7536 1.0257 5.8021 1.0619 7.8002 1.0695 4.7536 1.0000 1.1545
4.8203 1.0253 5.8260 1.0565 7.8083 1.0734 4.8203 1.0000 1.1545
4.8828 1.0194 5.8608 1.0510 7.8116 1.0753 4.8828 1.0000 1.1545
5.8833 1.0571 7.8148 1.0738 5.4510 1.0000 1.1545
5.9054 1.0569 7.8180 1.0749 5.4848 1.0000 1.1545

77
0.95
1.00
1.05
1.10
1.15
1.20
2.90 3.90 4.90 5.90 6.90 7.90 8.90 9.90
Ra
ln (N)
GL16- Variation of Ra for all cases of levels braced For 5 Bay (G+11),
One Level Braced
Two Level Braced
Three Level Braced
Bare Fr.
Fully Braced Fr.

78
Variation of Shear force in member 04 in partially braced frames
ln (N)
Bare Fr. Braced Fr.
ln (N) Rs ln (N) Rs ln (N) Rs Rs Rs
3.4340 0.9355 5.4510 1.1980 7.7592 1.2559 3.4340 1.0000 1.0611
3.6636 1.1328 5.4848 1.1243 7.7626 1.1899 3.6636 1.0000 1.0611
3.8501 1.0726 5.5683 1.0007 7.7715 1.1613 3.8501 1.0000 1.0611
4.0073 0.9971 5.5984 0.9400 7.7749 1.1615 4.0073 1.0000 1.0611
4.1431 0.9952 5.6276 0.9271 7.7782 1.1575 4.1431 1.0000 1.0611
4.2627 1.0031 5.6560 0.9142 7.7816 1.1552 4.2627 1.0000 1.0611
4.5218 1.0010 5.6836 0.9067 7.7849 1.1537 4.5218 1.0000 1.0611
4.6052 0.9989 5.7104 0.9042 7.7882 1.1534 4.6052 1.0000 1.0611
4.6821 0.9984 5.7366 0.9037 7.7915 1.1542 4.6821 1.0000 1.0611
4.7536 0.9983 5.8021 0.9043 7.8002 1.1638 4.7536 1.0000 1.0611
4.8203 0.9983 5.8260 0.9107 7.8083 1.0967 4.8203 1.0000 1.0611
4.8828 0.9986 5.8608 1.1644 7.8116 1.0883 4.8828 1.0000 1.0611
5.8833 1.1181 7.8148 1.0951 5.4510 1.0000 1.0611
5.9054 1.1138 7.8180 1.0938 5.4848 1.0000 1.0611
5.9269 1.1185 7.8212 1.0926 5.5683 1.0000 1.0611
5.9480 1.1171 7.8244 1.0917 5.5984 1.0000 1.0611

79
0.80
0.85
0.90
0.95
1.00
1.05
1.10
1.15
1.20
1.25
1.30
2.90 3.90 4.90 5.90 6.90 7.90 8.90 9.90
Rs
ln (N)
GL-17 Variation of Rs for all cases of levels braced For 5 Bay (G+11),
One Level Braced
Two Level Braced
Three Level Braced
Bare Fr.
Fully Braced Fr.

80
Variation of Bending Moment in member 04 in partially braced frames
ln (N)
Bare Fr. Braced Fr.
ln (N) Rm ln (N) Rm ln (N) Rm Rm Rm
3.4340 0.3516 5.4510 0.3334 7.7592 0.3519 3.4340 1.0000 0.3100
3.6636 0.5069 5.4848 0.3433 7.7626 0.3362 3.6636 1.0000 0.3100
3.8501 0.6269 5.5683 0.3322 7.7715 0.3250 3.8501 1.0000 0.3100
4.0073 0.7485 5.5984 0.3355 7.7749 0.3253 4.0073 1.0000 0.3100
4.1431 0.8849 5.6276 0.3430 7.7782 0.3251 4.1431 1.0000 0.3100
4.2627 0.9474 5.6560 0.3458 7.7816 0.3247 4.2627 1.0000 0.3100
4.5218 0.9782 5.6836 0.3467 7.7849 0.3244 4.5218 1.0000 0.3100
4.6052 0.9927 5.7104 0.3470 7.7882 0.3243 4.6052 1.0000 0.3100
4.6821 0.9972 5.7366 0.3472 7.7915 0.3245 4.6821 1.0000 0.3100
4.7536 0.9987 5.8021 0.3473 7.8002 0.3264 4.7536 1.0000 0.3100
4.8203 0.9991 5.8260 0.3481 7.8083 0.3401 4.8203 1.0000 0.3100
4.8828 0.9994 5.8608 0.4986 7.8116 0.3354 4.8828 1.0000 0.3100
5.8833 0.4910 7.8148 0.3366 5.4510 1.0000 0.3100
5.9054 0.4915 7.8180 0.3368 5.4848 1.0000 0.3100
5.9269 0.4968 7.8212 0.3367 5.5683 1.0000 0.3100

81
0.20
0.30
0.40
0.50
0.60
0.70
0.80
0.90
1.00
1.10
2.90 3.90 4.90 5.90 6.90 7.90 8.90 9.90
Rm
ln (N)
GL18- Variation of Rm for all cases of levels bracedFor 5 Bay (G+11),
Two Level Braced
Three Level Braced
Bare Fr.
Fully Braced Fr.

Internal Forces Acceptable range of (Ra/Rs/Rm)
Bracing Arrangements from Table
Satisfying Acceptable Range
One Bay Braced
Two Bay
Braced
Axial Force 0.92 to 1.15 1,2 4,6
shear Force 0.75 to 0.95 1,2 4
Bending Moment 0.32 to 0.55 1,2,3 4,5,6
All As Above 1,2 4
Optimized Frames symmetrical Cases 2 ----
Table A. Acceptable Range of (Ra/Rs/Rm) for 3 Bay (G+11) with various Bracing
arrangements for member no. 4

83
Case no.
QUANTITY COST in Rs
% of
Saving
Concrete(m3) Steel (kg) Concrete Steel Total
Bare 52.3 4659.105 261500/- 163068.68/- 424568.675/- ---
2 44.21 5261.92 221050/- 184167.2/- 405217.2/- 4.56%

84
Bare frame Case No.02
Optimum bracing pattern for 3-bay (G+11), Baywise bracing
pattern

85
Acceptable Range of (Ra/Rs/Rm) for 5 Bay (G+11) with various Bracing
Case No.
Acceptable range
of (Ra/Rs/Rm)
Bracing Arrangements from Table Satisfying Acceptable Range
One Bay Braced Two Bay Braced Three Bay Braced
Four Bay
Braced
Axial Force 0.9 to 0.99 1,2,3,4 6,7,8,10,11,13 16,17,19,22 26
shear Force 0.5 to 0.99 1,2,3 6,7,8,10,11,13 16,17,19,22 26
Bending Moment 0.25 to 0.65 1,2,3,4 6 to 15 16 to 25 26 to 30
All As Above 1,2,3 6,7,8,10,11,13 16,17,19,22 26
Optimized Frames symmetrical Cases 3 11 22 -----

86
Case no.
QUANTITY COST in Rs
%
SavingConcrete (m3) Steel (kg) concrete Steel Total
Bare 81.35 7539.98 406750/- 263899.3/- 670649.3/- ---
3 71.24 7810.521 356200/- 273368.235/- 629568.235/- 6.13%
11 75.82 7879.959 379100/- 275798.565/- 654898.565/- 2.35%

87
Bare Frame Case No.3 Case No.11
Figure 4.5 Optimum bracing pattern for 5-bay (G+11), Bay wise bracing pattern.

88
Table 4.10Acceptable Range of (Ra/Rs/Rm) for 7 Bay (G+11) with various Bracing Arrangements for member no. 8
Internal
Forces
Acceptable
range of
(Ra/Rs/Rm)
One Bay
Braced
Two Bay
Braced
Three Bay Braced Four Bay Braced
Five Bay
Braced
Six Bay
Braced
Axial
Force
0.90 to 0.99 1,2,3,4,5,6
8,9,10,11,12,14,
15,16,17,19,20,
21,23,24,26
29,30,31,32,34,35,36,38,
39,41,44,45,46,48,49,51,
54,55,57,60
64,65,66,68,69,71,7
4,75,77,80,84,85,87,
90,94
99,100,102,10
5,109,100
120
shear
Force
0.45 to 0.99 1,2,3,4,5
8,9,10,11,12,14,
15,16,17,19,20,
21,23,24
29,30,31,32,34,35,36,38,
39,41,44,45,46,48,49,51,
54,55,57,60
64,65,66,68,69,71,7
4,75,77,80,84,85,87,
90,94
99,100,101,10
2,105,109,
114, 115
120,121
Bending
Moment
0.23 to 0.65 1,2,3,4,5 8 to 28 29 to 63 64 to 98 99 to 119
120 to
126
All As Above 1,2,3,4,5
8,9,10,11,12,14,
15,16,17,19,20,
21,23,24
29,30,31,32,34,35,36,38,
39,41,44,45,46,48,49,51,
54,55,57,60
64,65,66,68,69,71,7
4,75,77,80,84,85,87,
90,94
99,100 ,102,
105, 109, 114
120
Optimized
Frames
Symmetrical
Cases
4 17, 20 49,54 87 114 -----

89
Case no.
QUANTITY COST in Rs % of
Saving
Concrete (m3) Steel (kg) concrete Steel Total
Bare 108.78 10417.474 543900/- 364611.59/- 908511.59/- ---
4 92.35 11281.734 461750/- 394860.69/- 856610.69/- 5.71%
17 99.44 10905.188 497200/- 381681.58/- 878881.58/- 3.26%
20 101.24 10727.949 506200/- 375478.215/- 881678.215/- 2.95%
87 100.87 10932.403 504350/- 382634.11/- 886984.105/- 2.37%

90
Bare Case No.4 Case No.17
Figure 4.6 Optimum bracing pattern for 7-bay (G+11), Bay wise bracing pattern.

91
OPTIMUM BRACING LOCATION FOR LEVELWISE OPTIMIZATION
Acceptable Range of (Ra/Rs/Rm) for 5 Bay (G+5) with various Bracing
Internal
Forces
Acceptable
range of
(Ra/Rs/Rm)
One Level
Braced
Two Level
Braced
Three Level
Braced
Four Level
Braced
Five
Level
Braced
Axial Force 1.02 to 1.13 1 to 5 7 to 21 22 to 41 42 to 56
57 to
62
shear Force 0.98 to 1.09 1, 3 to 6
8 to 13, 16 to
21
26 to 36, 38 to
41
48 to 56
59,
61,62
Bending
Moment
0.35 to 0.65 1,2 7 to 15 22 to 37 42 to 55
57 to
62
All As Above 1 8 to 13 26 to 36 48 to 55
59,
61,62

92
Case no.
QUANTITY COST in Rs % Of
Concrete (m3) Steel (kg) Concrete Steel Total Saving
Bare 39.74 2829.188 198700/- 99021.58/- 297721.58/- ---
1 26.84 3236.41 134200/- 113274.35/- 247474.35/- 16.88%
10 28.4 3439.284 142000/- 120374.94/- 262374.94/- 11.87%
11 28.4 3509.157 142000/- 122820.5/- 264820.495/- 11.05%

93
Bare Frame
Case No.01 Case No.10 Case No.11
Figure 4.7 Optimum bracing pattern for 5-bay (G+5), Levelwise bracing pattern

94
Optimum bracing location for level wise optimization of 5-bay, (G+8) structure:
Acceptable Range of (Ra/Rs/Rm) for 5 Bay (G+8) with various Bracing arrangements
for member no. 4
Internal Forces
Acceptable
range of
(Ra/Rs/Rm)
One Level Braced Two Level Braced
Three Level
Braced
Axial Force 1.00 to 1.08 1 to 12 13 to 78
79 to 118, 120 to
123, 125 to 127,
129, 130, 132 to
298
shear Force 0.86 to 0.99 1 16 to 23, 43
98 to 133, 215 to
221
Bending Moment 0.32 to 0.55 1, 2 13 to 33 79 to 178
All As Above 1 16 to 23
98 to 118, 120 to
123, 125, 126,
127, 129, 130,
132, 133

95
Case no.
QUANTITY COST in Rs
% Of
Saving
Concrete (m3) Steel (kg) Concrete Steel Total
Bare 58.41 4774.744 292050/- 167116.04/- 459166.04/- ---
1 45.06 5266.34 225300/- 184321.94/- 409621.94/- 10.79%
12 47.17 5341.86 235850/- 186965.14/- 422815.14/- 7.92%
64 48.88 5295.15 244400/- 185330.18/- 429730.18/- 6.41%

97
Optimum bracing location for levelwise optimization of 5-bay, (G+11) structure:
Acceptable Range of (Ra/Rs/Rm) for 5 Bay (G+11) with various Bracing arrangements
for member no. 4
Internal Forces
Acceptable range
of (Ra/Rs/Rm)
One Level Braced Two Levels Braced
Three Levels
Braced
Axial Force 1.00 to 1.08 1 to 12 13 to 78
79 to 118, 120 to
123, 125 to 127,
129, 130, 132 to
298
shear Force 0.86 to 0.99 1 16 to 23, 43
98 to 133, 215 to
221
Bending Moment 0.32 to 0.55 1, 2 13 to 33 79 to 178
All As Above 1 16 to 23
98 to 118, 120 to
123, 125, 126,
127, 129, 130,
132, 133

98
Case no.
QUANTITY COST in Rs
% Of
Saving
Concrete
(m3)
Steel (kg) Concrete Steel Total
Bare 81.35 7539.98 406750/- 263899.3/- 670649.3/- ---
1 67.36 8118.43 336800/- 284145.05/- 620945.05/- 7.41%
16 69.27 8057.68 346350/- 282018.8/- 628368.8/- 6.30%
98 72.12 7846.72 360600/- 274635.16/- 635235.17/- 5.28%

101
Partially Braced Frames
Typical Frame with Outrigger showing the
bracing combinations of braces

102
Case no.
Quantity Cost in Rs
% SavingConcrete
(m3)
Bare 81.35 7891.319 406750/- 27616/- 682946/- ---
C+8 72.77 7617.22 363850/- 266602.7/- 630452.7/- 6.00%
C+6 73.45 7571.712 367250/- 265009.2/- 632259.92/- 5.72%
C+9 72.77 7674.173 363850/- 268596.055/_ 632446.055 5.70%
C+7 72.77 7682.86 363850/- 268900.1/- 632750.1 5.65%
C+11 73.45 7585.244 367250/- 265483.54/- 632733.54 5.65%

103
Case no. C+8 Case no.C+6 Case no.C+9
Optimum bracing pattern for 5-bay (G+11), outrigger bracing
pattern.

104
Case no.
Quantity Cost in Rs
%
Saving
Concrete
(m3)
Bare 81.35 7891.319 406750/- 027616.00/- 682946/- ---
2+4 & 6 77.64 7796.102 388200/- 272863.57/- 661063.57/- 1.43%
2+4 & 8 76.43 8028.503 382150/- 280997.60/- 663147.605/- 1.12%

105
Case no.2+4+6 Case no.2+4+8
Optimum bracing pattern for 5-bay (G+11), outrigger bracing pattern.

107
Cellwise Braced Frames
Figure showing typical frame for single cell
bracing pattern

109
Cellwise bracing – moving levelwise
A) Single Cell Braced at a Time
Cell Braced
QUANTITY COST in
% Of
Saving
Concrete
(m3)
Bare 81.35 7539.98 406750/- 263899.30/- 670649.30/- ---
4 65.84 7975.84 329200/- 279154.33/- 608354.33/- 9.29%
7 67.72 7713.42 338600/- 269969.70/- 608569.70/- 9.26%
3 67.72 7729.88 338600/- 270545.91/- 609145.91/- 9.17%
Central bay
braced
71.24 7810.52 356200/- 273368.24/- 629568.24/- 6.13%

110
Braced Cell No.04 Braced Cell No.07 Braced Cell No.03
Figure 4.13 Optimum bracing pattern for 5-bay (G+11), single cell braced pattern.

111
B) Two Cells Braced at a Time
Cell Braced
QUANTITY COST in `
% Of
Saving
Concrete
(m3)
Bare 81.35 7539.98 406750/- 263899.30/- 670649.30/- ---
1+6 68.1 7653.816 340500/- 267883.56/- 608383.56/- 9.28%
1+4 68.1 7685.263 340500/- 268984.21/- 609484.21/- 9.12%
2+5 68.1 7693.362 340500/- 269267.67/- 609767.67/- 9.08%

112
Braced Cell No. 1&6 Braced Cell No.1&4 Braced Cell No. 2&5
Figure 4.14 Optimum bracing pattern for 5-bay (G+11), two cells braced pattern.

113
C) Three Cells Braced at a Time
Cell Braced
QUANTITY COST in `
% Of
Saving
Concrete
(m3)
Bare 81.35 7539.98 406750/- 263899.30/- 670649.30/- ---
2+5+8 68.49 7663.644 342450/- 268227.54/- 610677.54/- 8.94%
1+4+6 68.49 7676.998 342450/- 268694.93/- 611144.93/- 8.87%
2+4+6 68.49 7760.805 342450/- 271628.18/- 614078.18/- 8.44%

114
Braced Cell 2+5+8 Braced Cell 1+4+6 Braced Cell 2+4+6
Figure 4.15 Optimum bracing pattern for 5-bay (G+11), three cells braced pattern.

115
Cellwise bracing – moving baywise:
For 5 bay G+11cellwise bracing – moving baywise:
A) Ground Floor Braced:
Case no.
QUANTITY COST in `
% Of
Saving
Concrete
(m3)
Bare 81.35 7539.98 406750/- 263899.30/- 670649.30/- ---
Braced cell 3 67.72 7785.25 338600/- 272483.58/- 611083.58/- 8.88%
Braced cell
2+4
68.10 7771.47 340500/- 272001.48/- 612501.49/- 8.67%
Braced cell
1+3+5
68.49 7778.99 342450/- 272264.55/- 614714.55/- 8.34%

116
Braced Cell 3 Braced Cell 2+4 Braced Cell 1+3+5
Figure 4.16 Optimum bracing pattern for 5-bay (G+11), Ground floor level braced.

117
B) Fourth Floor Braced:
Case no.
QUANTITY COST in `
% Of
Saving
Concrete
(m3)
Bare 81.35 7539.98 406750/- 263899.30/- 670649.30/- ---
Braced cell 3
65.84 7975.838 329200/- 279154.33/- 608354.33/- 9.29%
Braced cell
2+4
68.10 7699.495 340500/- 269482.33/- 609982.33/- 9.05%
Braced cell
1+3+5
68.49 7592.525 342450/- 265738.38/- 608188.38/- 9.31%

118
Figure 4.17 Optimum bracing pattern for 5-bay (G+11), First floor level braced.

119
C) Sixth Floor Braced
Case no.
QUANTITY COST in `
% Of
Saving
Concrete
(m3)
Bare 81.35 7539.98 406750/- 263899.3/- 670649.3/- ---
Braced cell
3
67.72 7713.42 338600/- 269970.0/- 608570.0/- 9.26%
Braced cell
2+4
68.1 7711.14 340500/- 269890.0/- 610390.0/- 9.00%
Braced cell
1+3+5
68.49 7635.75 342450/- 267251.0/- 609701.0/- 9.09%

120
Figure 4.18 Optimum bracing pattern for 5-bay (G+11), Second floor level braced.

121
Combination if cellwise bracing – moving levelwise and baywise:
Case no.
QUANTITY COST in `
% Of
Saving
Concrete
(m3)
Bare 81.35 7539.98 406750/- 263899.30/- 670649.30/- ---
Trial 1 68.49 7644.75 342450/- 267566.22/- 610016.22/- 9.04%
Trial 2 68.49 7659.07 342450/- 268067.45/- 610517.45/- 8.97%
Trial 3 68.49 7674.91 342450/- 268621.68/- 611071.68/- 8.88%
Trial 4 68.49 7722.63 342450/- 270291.88/- 612741.88/- 8.63%

122
Trial 1 Trial 2 Trial 3 Trial 4
Figure 4.19 Optimum bracing pattern for 5-bay (G+11), arbitrary bracing pattern.

123
VARIATION OF DISPLACEMENT IN STRUCTURE
Table TD-1 Variation of lateral displacement along height of structure for 3 Bay G+11
with 350 mm beam depth
Analysed
Structure
For 3 Bay G+11 350 mm beam Depth
Ht. From Base
(m)
Bare Frame
Fully Braced Frame
Optimum Bay
Braced
0 0.00 0.00 0.00
2.44 1.04 0.64 0.69
5.44 4.11 1.44 1.95
8.44 8.68 2.22 3.52
11.44 14.21 2.98 5.28
14.44 21.20 4.11 7.47
17.44 29.23 5.18 9.88
20.44 37.54 6.18 12.40
23.44 45.91 7.24 15.03
26.44 53.59 8.20 17.65
29.44 60.30 9.04 20.19
32.44 65.80 9.79 22.61
35.44 69.72 10.38 24.82
38.44 72.36 10.91 26.88

124
0
10
20
30
40
50
60
70
80
0 5 10 15 20 25 30 35 40 45
Displacement(mm)
Height From Base (m)
GD-1
Variation of lateral Displacement along height of
Structure 3 Bay (G+11) with 350 mm beam depth (L/C 7)
For Bare Fr.
For Fully Braced Fr.
Optimum Bay Braced Fr.

125
Table TD-2 Variation of lateral displacement along height of structure for 5 Bay G+11 with 350
mm beam depth
Analysed
Structure
Ht. From Base
(m)
Bare Frame Fully Braced
Frame
Optimum Bay
Braced
Optimum Level
Braced
0 0.00 0.00 0.00 0.00
2.44 1.05 0.66 0.74 0.59
5.44 4.14 1.48 2.27 1.68
8.44 8.72 2.26 4.31 4.17
11.44 14.23 3.00 6.62 8.04
14.44 21.12 4.13 9.44 13.88
17.44 28.95 5.18 12.55 21.20
20.44 36.98 6.13 15.78 28.97
23.44 45.00 7.14 19.13 36.88
26.44 52.32 8.01 22.44 44.15
29.44 58.58 8.74 25.61 50.40
32.44 63.56 9.33 28.56 55.38
35.44 67.10 9.77 31.21 58.92
38.44 69.57 10.13 33.63 61.40

126
0
10
20
30
40
50
60
70
80
0 5 10 15 20 25 30 35 40 45
Displacement(mm)
GD-2
For Bare Fr.
Optimum Level Braced Fr.

127
Table TD-3 Variation of lateral displacement along height of structure for 7 Bay G+11 with 350 mm
beam depth
Analysed Structure For 7 Bay G+11 350 mm beam Depth
Ht. From Base (m) Bare Frame
Fully Braced Frame
Optimum Bay
Braced
0 0.00 0.00 0.00
2.44 1.05 0.67 0.77
5.44 4.15 1.49 2.51
8.44 8.72 2.27 4.88
11.44 14.22 3.00 7.61
14.44 21.07 4.13 10.91
17.44 28.80 5.18 14.56
20.44 36.70 6.12 18.33
23.44 44.58 7.11 22.23
26.44 51.77 7.97 26.05
29.44 57.97 8.68 29.67
32.44 62.99 9.27 33.04
35.44 66.47 9.71 36.02
38.44 68.81 10.06 38.64

128
0
10
20
30
40
50
60
70
80
0 5 10 15 20 25 30 35 40 45
Displacement(mm)
GD-3
For Bare Fr.

129
Table TD-4 Variation of lateral displacement along height of structure for 5 Bay G+11 with 350
mm beam depth
Analysed
Structure
Ht. From Base
(m)
Bare Frame Fully Braced
Frame
Frame with
Outrigger
Cellwise Braced
Frame
0 0.00 0.00 0 0
2.44 1.05 0.66 0.742 1.001
5.44 4.14 1.48 2.208 3.812
8.44 8.72 2.26 4.104 7.848
11.44 14.23 3.00 6.228 12.47
14.44 21.12 4.13 8.767 17.104
17.44 28.95 5.18 11.456 21.031
20.44 36.98 6.13 14.141 26.214
23.44 45.00 7.14 16.706 32.898
26.44 52.32 8.01 18.584 39.709
29.44 58.58 8.74 19.837 45.76
32.44 63.56 9.33 21.164 50.636
35.44 67.10 9.77 22.669 54.116
38.44 69.57 10.13 24.111 56.538

130
0
10
20
30
40
50
60
70
80
0 5 10 15 20 25 30 35 40 45
Displacement(mm)
GD-4
Variation of lateral Displacement at various level
For Bare Fr.
Optimum Outrigger Fr.
Cellwise Braced Fr.

131
Conclusions:
Based on Numerous Analysis Carried out the following Conclusions are
Drawn.
About bare frame
Column segments at lower level attract larger axial forces as compared to bay variation
i.e. as number of bays going to increase the axial forces in the column at bottom segments
increases. The same is with bending moment.
The considered parameters such as axial force, shear force and bending moments are
more as compared to other cases of braced frames.
As number of storey increases the axial forces, bending moments and shear forces in the
column at bottom segments increase. As number of bays for a given height of frame
increases, of above internal forces only axial force is found to change commensurate with
it. The other two almost remain constant.
It also concludes that for high rise structures, the higher axial forces and deformations
especially in the columns, and concentration of them over a greater height may cause
bending moment parameter to become predominant.
The lateral displacements are well within the acceptable limit as per IS 1893:2002(10).

132
About Fully Braced Frame
Axial force in the worst loaded column increases as compared to bare frame by 14% to 15%
irrespective of the number of bays for a G+11 structure. For a given number of bays the
structure attracts the axial force optimally for a certain aspect ratio of the frame. In case of a 5
bay structure it is found as 1.022 and the corresponding rise in axial force is 13.02%.
Axial forces attracted by column segments at upper levels are independent of stiffness of
beam.
Axial forces in columns increases as compared to bare frames.
Bending moments in column are substantially reduced as compared to bare frames.
Economy is independent of the beam stiffness.
Braces are found to carry large axial forces as compared with shear forces and bending
moments, which are insignificantly small.

1
3
3
About Fully Braced Frame
It is also found that shear force in the penultimate column is greater than
shear force in the end column of the same structure. The same case is with
axial force.
Axial force in brace in given structure increases and decreases alternately
at higher level and a lower level it varies conversely.
Lateral displacements in such frames are tremendously reduced as
compared to bare frames of the same geometry, which are already in the
permissible limit.

134
About Partially braced frames
For 5 Bay G+11 structure that are braced along given number of bays with V type bracing are
found to be economical due to reduction in the column cross sections.
Bending moment is getting reduced for worst loaded columns.
The substantial reduction in bending moment for worst loaded column leads to section
reduction.
Axial force in such column segments is increased.
In case of combinations partially braced frames it is seen that when bay wise bracing is
provided by keeping equal spacing offer more economy but it will give more economy in the
case of cell wise bracing when provided closely.
Such structures are economical than bare frames but not as compared to cell wise braced
frames. Maximum economy is found to be 6.13% as compared to bare frame which is nearly
43% less than cell wise braced frame.

Books:
Chopra A.K., (1997) “Dynamics of structure”, 2nd Ed., Prentice Hall of India Pvt.
Ltd., New Delhi.
Dr. V. L. Shah and Dr. S.R. Karve, (Feb. 2005), “Illustrated design of reinforced
concrete building”, 5th Ed., structure publication.
Mario Paz, (1987) “Structural Dynamics”, 2nd Ed., CBS publishers.
Ram Chandra, (1992) “Design of steel structures”, 10th Ed., Standard Book House,
Delhi
V.N. Vazirani and M.M. Ratawani, (1985) “Analysis of structures”, 10th Ed.,
Khanna Publishers.
Weaver Jr. and Gere J.M., (1986) “Matrix analysis of framed structure”, CBS
Publishers and distributor, New Delhi.

136
I.S. codes:
I.S. 456-1993, Indian standard code of practice for plain and reinforced concrete
(fourth revision), Bureau of Indian standards, New Delhi.
I.S. 875 (part I): 1987, Indian standard code of practice for design loads (other than
earthquake) for buildings and structures, Bureau of Indian standards, New Delhi.
I.S. 875 (part II): 1987, Indian standard code of practice for design loads (other than
earthquake) for buildings and structures, Bureau of Indian standards, New Delhi.
I.S. 1893(Part 1)-2002, Criteria for earthquake resistant design of structure, general
provision and building, Bureau of Indian standards, New Delhi.
I.S. 4326-2000, Indian standard code of practice for earthquake resistant design and
construction of buildings, Bureau of Indian standards, New Delhi.
I.S.13920: 1993, Indian standard code of practice for ductile detailing of Reinforced
concrete structure subjected to seismic forces, Bureau of Indian Standards, New Delhi.

137
Journals/symposia:
A. R. Khaloo & M. Mahdi Mohseni, “Nonlinear Seismic Behaviour of RC Frames
with RC Braces” Asian Journal of Civil Engineering, Vol. 9, No. 6 (2008).
A.A.Shish Ranka, Arathy Gopal, RahuL Jee, “Earthquake Resistant Building
Design Seminar Report”
J.P. Desai, A.K. Jain and A.S. Arya, “Seismic response of R.C. Braced Frames”,
Computers and Structures Vol. 29, No. 4 (1987).
Mahmoud R. Maheri, R. Akbari, “seismic behaviour factor, for steel x-braced and
knee-braced rc buildings”, Engineering Structures, Volume 25, Issue 12, October
2003, Pages1505-1513.
Yunfei H., Yufeng C., Chang, S., and Bainian H., “The Experimental Study of a
Two-Bay Three Story Reinforced Concrete Frame Under Cyclic Loading”,
Proceedings of the Eighth Symposium on Earthquake Engineering, Roorkee, India
(1986).

138
U.G. Projects:
Bhise A. T. et al, “Computer Aided Analyses of Multistoreyed building frames
with Beams of Varying Inertia” U.G. project, C.E.D., W.I.T., Solapur, India, 1997.
 Bansode M. A. et al, “Computer Aided Analyses of Multistoreyed building
frames with Beams of varying Inertia” U.G. project, C.E.D., W.I.T., Solapur, India,
1999.
Diddi J. D. et al “Computer Aided Analyses of Multistoreyed building frames
subjected to earthquake forces” U.G. project, C.E.D., W.I.T., Solapur, India, 2002.
Rajput D. H. et al “Computer Aided Analyses of Multistoreyed building frames
subjected to gravity and seismic loads considering beams of varying inertia” U.G.
project, C.E.D., W.I.T., Solapur, India, 2008.

139
P.G. Projects:
Bhise A.T., “Computer aided analysis of multistoreyed building frames with beams of varying inertia
and changing stiffness. P.G. dissertation, C.E.D. W.I.T. Solapur (M.S.), India, 2007.
Boga S. A. “Analyses of Multistoreyed ‘V’ Braced building frames with Beams of changing stiffness
subjected to seismic and gravity loading”, P.G. dissertation, C.E.D., W.I.T., Solapur (M.S.), India, 2009
(Unpublished).
Chopde K. Y. worked on “Analyses of Multistoreyed ‘V’ Braced frames with Beams of Varying inertia
subjected to seismic and gravity loading”, P.G. dissertation, C.E.D., W.I.T., Solapur (M.S.), India, 2009
(Unpublished).
Kore S. B. “Analysis of Multistoreyed Braced frames subjected to seismic and gravity loading”. P.G.
dissertation, C.E.D., W.I.T. Solapur (M.S.), India, 2006
Pawar D. S., “Analysis of Multistoreyed ‘A’ & ‘V’ type Braced Frames Subjected to Seismic and
Gravity Loading.” P.G. dissertation, C.E.D. W.I.T. Solapur (M.S.), India, 2008.
Talekar S. N., “Analyses of Diagonally braced Multistoreyed Building frames with Beams of Changing
stiffness subjected to gravity and earthquake loading”, P.G. dissertation, C.E.D., W.I.T., Solapur (M.S.),
India, 2009 (Unpublished).

140
Software’s:
STAAD- structural analysis and design commercial software.
Websites:
MULTI-STOREY BUILDINGS – I
MULTI-STOREY BUILDINGS – II
http://www.steel-insdag.org/new/pdfs/chapter38.pdf
http://www.steel-insdag.org/new/pdfs/chapter37.pdf
http://www.gogetpapers.com/Papers/braced_frame
http://en.wikipedia.org/wiki/Structural_analysis
http://en.wikipedia.org/wiki/File:ExteiorShearTruss.jpg
Analysis for Building Frames
http://www.mahapwd.com/training/buildingdesign/16.htm

Dissertation report

More Related Content

What's hot

Viewers also liked

Similar to Dissertation report

More from Pralhad Kore

Recently uploaded

Dissertation report