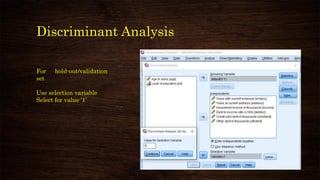
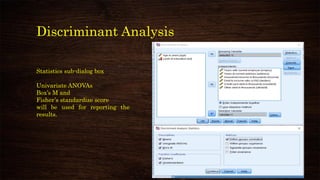
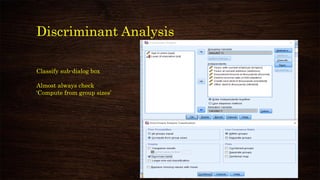
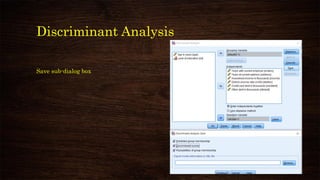
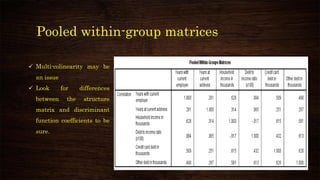
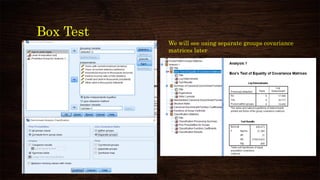
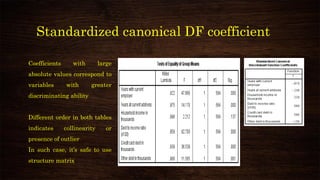
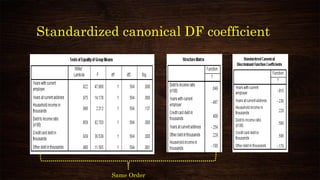
This document provides an overview and agenda for a presentation on multivariate analysis and discriminant analysis using SPSS. It introduces the presenter, Dr. Nisha Arora, and lists her areas of expertise including statistics, machine learning, and teaching online courses in programs like R and Python. The agenda outlines concepts in discriminant analysis and how to perform it in SPSS, including data preparation, assumptions, interpretation of outputs, and ways to improve the analysis model.

1. MULTIVARIATE
ANALYSIS
- Dr Nisha Arora

2. About Me Concepts
How it Works? Q/A Session
Agenda

3. • Dr. Nisha Arora is a proficient educator, passionate trainer,
You Tuber, occasional writer, and a learner forever.
✓ PhD in Mathematics.
✓ Works in the area of Data Science, Statistical
Research, Data Visualization & Storytelling
✓ Creator of various courses
✓ Contributor to various research communities and
Q/A forums
✓ Mentor for women in Tech Global
3
About Me
An educator by heart & a
trainer by profession.

4. http://stats.stackexchange.com/users/79100/learner
https://stackoverflow.com/users/5114585/dr-nisha-arora
https://www.quora.com/profile/Nisha-Arora-9
https://www.researchgate.net/profile/Nisha_Arora2/contributions
http://learnerworld.tumblr.com/
https://www.slideshare.net/NishaArora1
https://scholar.google.com/citations?user=JgCRWh4AAAAJ&hl=en&authuser=
1
https://www.youtube.com/channel/UCniyhvrD_8AM2jXki3eEErw
https://groups.google.com/g/dataanalysistraining/search?q=nisha%20arora
https://www.linkedin.com/in/drnishaarora/detail/recent-activity/posts/
✓ Research Queries
✓ Coding Queries
✓ Blog Posts
✓ Slide Decks
✓ My Talks
✓ Publications
✓ Lectures
✓ Layman’s Term
Explanation
✓ Mentoring
✓ Articles & Much More
My Contribution to the Community

5. ❖ Statistics
❖ Data Analysis
❖ Machine Learning
❖ Analytics & Data Science
❖ Data Visualization & Storytelling
❖ Mathematics & Operations Research
❖ Online Teaching
❖ Excel/SPSS/R/Python/Shiny
❖ Tableau/PowerBI
My Expertise

6. Connect With Me
HTTPS://WWW.LINKEDIN.COM/IN/DRNISHAARORA /
DR.ARORANISHA@GMAIL.COM .

7. Discriminant Analysis
USING SPSS

8. My answer to ‘classification of multiple outcomes
with categorical and continuous predictors’:
https://stats.stackexchange.com/a/513616/79100

9. When to use LDA?
✓ Non-Ordinal response variable
✓ Metric predictors
✓ Works well for low sample size
✓ Works well when cases are well separable
✓ More restrictive than logistic regression

10. Assumptions of LDA
✓ Both LDA and QDA assume the predictor variables X are
drawn from a multivariate Gaussian distribution.
✓ LDA assumes equality of covariances among the predictor
variables X across each all levels of Y
✓ LDA and QDA require the number of predictor variables (p) to
be less then the sample size (n). A simple rule of thumb is to
use LDA & QDA on data sets where n ≥ 5p

11. Default Prediction
✓ The information on 700 past customers is contained in
bankloan.sav
✓ These are the customers who were previously given loans.
✓ Use a random sample of these 80% customers to create a
discriminant analysis model, setting the remaining customers
aside to validate the analysis.
✓ Then use the model to classify the remaining 20% prospective
customers as good or bad credit risks.

12. Data Preparation for LDA
To replicate my
results

13. Data Preparation for LDA
Creating a new
variable for training
and validation set

14. Discriminant Analysis
Analyze → Classify →
Discriminant

15. Discriminant Analysis
✓ Grouping variable –
Categorical response
variable
✓ Define Range – As per
number of categories
[see coding in variable
view]
✓ Independents – Metric
predictors
✓ How to choose
predictors –
✓ Domain knowledge
✓ Previous research
✓ EDA
✓ Step-wise

16. Discriminant Analysis
For hold-out/validation
set
Use selection variable
Select for value ‘1’

17. Discriminant Analysis
Statistics sub-dialog box
Univariate ANOVAs
Box’s M and
Fisher’s standardize score
will be used for reporting the
results.

18. Discriminant Analysis
Classify sub-dialog box
Almost always check
‘Compute from group sizes’

19. Discriminant Analysis
Save sub-dialog box

20. Case processing summary
✓ No missing values
✓ Here model is trained on 566 observations
& 134 are unselected cases (hold-out set)

21. Group Statistics
Observe if variables are discriminating the
response
Larger std indicates issues with predictors,
specifically income & debt to income ratio.
You may want to transform these predictors

22. Test of equality of group means
✓ All predictors are contributing to the model
except household income
✓ Wilk’s lambda values (unexplained varation in
each predictor by groups of response variable)
is higher
✓ The table suggests that Debt to income ratio
(x100) is best, followed by Years with current
employer, Credit card debt in thousands, and
Years at current address, and then other debts

23. Pooled within-group matrices
✓ Multi-colinearity may be
an issue
✓ Look for differences
between the structure
matrix and discriminant
function coefficients to be
sure.

24. Box Test
Box's M tests
Null Hypothesis: Equality of covariances
across groups
P-value < alpha (0.05)
Null Rejected
Use separate matrices to see if it gives
radically different classification results.
We will see using separate groups covariance
matrices later

25. Summary of Canonical Discriminant Functions
✓ Eigen Value - Higher the better
✓ Canonical Correlation- Pearson's correlation between
the discriminant scores and the groups. Higher the
better
✓ Wilks' lambda - It measures how well each function
separates cases into groups.
Smaller values of Wilks' lambda indicate greater
discriminatory ability of the function.
✓ Associated chi-square tests- Null: the means of the
functions listed are equal across groups
P-value < 0.05 the discriminant function does better than
chance at separating the groups.

26. Standardized canonical DF coefficient
Coefficients with large
absolute values correspond to
variables with greater
discriminating ability
Different order in both tables
indicates collinearity or
presence of outlier
In such case, it’s safe to use
structure matrix

27. Standardized canonical DF coefficient
Same Order

28. Canonical Discriminant Function Coefficients
Used for writing equation & computing
discriminant function for each predictor

29. Functions at Group Centroids
Used for determining cut-off value

30. Discriminant Analysis_ Outputs
Classification functions
✓ The classification functions are used to assign cases to groups.
✓ There is a separate function for each group. For each case, a
classification score is computed for each function.
✓ The discriminant model assigns the case to the group whose
classification function obtained the highest score.

31. Discriminant Analysis _Output
The within-groups correlation matrix
shows the correlations between the
predictors. The largest correlations
occur between Credit card debt in
thousands and the other variables, but
it is difficult to tell if they are large
enough to be a concern. Look for
differences between the structure
matrix and discriminant function
coefficients to be sure.

32. Discriminant Analysis _Output
Box's M tests the assumption of equality of covariances
across groups. Log determinants are a measure of the
variability of the groups. Larger log determinants
correspond to more variable groups. Large differences in
log determinants indicate groups that have different
covariance matrices.
Since Box's M is significant, you should request separate
matrices to see if it gives radically different classification
results. See the section on specifying separate-groups
covariance matrices for more information.

33. Discriminant Analysis _Output
There are several tables that assess
the contribution of each variable to the
model, including the tests of equality of
group means, the discriminant function
coefficients, and the structure matrix

34. Discriminant Analysis _Output
The standardized coefficients allow you
to compare variables measured on
different scales. Coefficients with large
absolute values correspond to variables
with greater discriminating ability.
This table downgrades the importance
of Debt to income ratio (x100), but the
order is otherwise the same.

35. Prior Probabilities for Groups
A prior probability is an estimate of the
likelihood that a case belongs to a
particular group when no other
information about it is available

36. Classification Function Coefficients
These are used to compute
probabilities for group membership.

37. Classification Results
Training set accuracy = 82.2%
Validation set accuracy = 78.4%

38. How to improve model
Use variable selection
In SPSS, step-wise method
Use separate case covariance matrix

39. Discriminant Analysis
Since Box's M is significant, it's worth
running a second analysis to see
whether using a separate-groups
covariance matrix changes the
classification.

40. Discriminant Analysis _Output
The structure matrix shows the correlation of each predictor variable with the
discriminant function. The ordering in the structure matrix is the same as that suggested
by the tests of equality of group means and is different from that in the standardized
coefficients table. This disagreement is likely due to the collinearity between Years with
current employer and Credit card debt in thousands noted in the correlation matrix.
Since the structure matrix is unaffected by collinearity, it's safe to say that this
collinearity has inflated the importance of Years with current employer and Credit card
debt in thousands in the standardized coefficients table. Thus, Debt to income ratio
(x100) best discriminates between defaulters and nondefaulters.

41. Discriminant Analysis _Output
In addition to measures for checking
the contribution of individual
predictors to your discriminant model,
the Discriminant Analysis procedure
provides the eigenvalues and Wilks'
lambda tables for seeing how well the
discriminant model as a whole fits the
data.

42. Discriminant Analysis _Output
The eigenvalues table provides
information about the relative efficacy
of each discriminant function. When
there are two groups, the canonical
correlation is the most useful measure
in the table, and it is equivalent to
Pearson's correlation between the
discriminant scores and the groups.

43. Discriminant Analysis _Output
Wilks' lambda is a measure of how well each function
separates cases into groups. It is equal to the
proportion of the total variance in the discriminant
scores not explained by differences among the groups.
Smaller values of Wilks' lambda indicate greater
discriminatory ability of the function.
The associated chi-square statistic tests the hypothesis
that the means of the functions listed are equal across
groups. The small significance value indicates that the
discriminant function does better than chance at
separating the groups.

44. Discriminant Analysis _Output
The classification table shows the practical
results of using the discriminant model. Of
the cases used to create the model, 94 of
the 124 people who previously defaulted are
classified correctly. 281 of the 375
nondefaulters are classified correctly.
Overall, 75.2% of the cases are classified
correctly.
Classifications based upon the cases used to
create the model tend to be too "optimistic"
in the sense that their classification rate is
inflated. The cross-validated section of the
table attempts to correct this by classifying
each case while leaving it out from the
model calculations; however, this method is
generally still more "optimistic" than subset
validation.

45. Discriminant Analysis _Output
Rest all tables are same.
The classification results have not
changed much, so it's probably not
worth using separate covariance
matrices. Box's M can be overly
sensitive to large data files, which is
likely what happened here.

46. Using z-scores

47. Get your hands dirty!
Play around with different models & see what works best for your problem

48. How to report the results?
1. ANOVA Table [univariate anova in statistics sub dialog box)
relation of individual predictor
2. BOX M (Assumption checking)
it's not very strong measure...for large sample, mostly, it gives p value >
0.05
3. Performance (Eigen Value, Wilks lambda, Classification table)
4. Discriminant equations & centroid scores
5. Relative importance

49. Multiple Discriminant Analysis
Data set: Iris.sav
Response variable = Species _ 3 categories (stored as string variable)
Iris-setosa, Iris-versicolor, and Iris-virginica
Alternate technique: Multonominal logistic regression
For MDA, we need to convert string variable to categorical variable
STEPS: Click Transform > Automatic Recode.
Double-click variable State in the left column to move it to the Variable -> New Name box.
Enter a name for the new, recoded variable in the New Name field, then click Add New Name.
Check the box for Treat blank string values as user-missing.
Click OK to finish.

50. Group Statistics

51. Box M
No need for separate group

52. Summary of Canonical Discriminant Functions

53. Variable Importance

54. Canonical Discriminant Functions

55. Functions at Group Centroids

56. Prior Probabilities for Groups

57. Classification Function Coefficients

58. Classification Results
Using leave-one-out cross validation

59. Combined Group Plot

60. Thank You