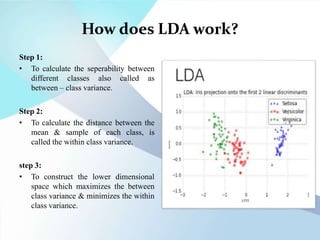
Discriminant function analysis (DFA) is a statistical technique used to determine which variables are best at predicting group membership. It creates linear combinations of predictor variables called discriminant functions that discriminate between categories of a dependent variable. DFA is similar to regression and ANOVA. It works by maximizing between-group differences and minimizing within-group differences to classify cases into groups based on predictor variables. The assumptions of DFA include normally distributed predictors and equal variance-covariance matrices within groups.

1. Discriminant functionanalysis(DFA) in R
Presented by
Priya dharshan

3. What is discriminant function analysis?
 DAis a statistical method
 Used by researches to help them understand the relationship between a
“dependent variable” & one/ more “independent variables”.
 DAis similar to regression analysis (RA) & analysis of variance (ANOVA)
 DFA is useful in determining whether a set of variables is effective in
predicting category membership.

4. What are discriminant functions?
Discriminant analysis works by creating one or more linear combinations
of predictors, creating a new latent variable for each function. These
functions are called as “discriminant functions”.

5. Why do we use DA?
 DA has various benefits as a statistical tool and is quite similar to
regression analysis.
 It can be used to determine which predictor variables are related to the
dependant variable and to predict the value of the dependant variable given
certain values of the predictor Variables.

6. When to use DA
 Data must be from different groups. Membership of group should be
already known before the starting analysis.
 It is used for the analysis of differences in groups.
 It is used for classification of new objects.

7. Purposeof DA
The objective of DA is to develop discriminant functions that are nothing
but the linear combination of independent variables that will discriminate
between the categories of the dependent variable in a perfect manner.

8. Basics of DFA
Discriminating variables (predictors):
independent variables which construct a discriminant function
Dependent variable (criterion variable):
 Object of classification on the basis of independent variables
 Needs to be categorical
 Known as grouping variables in SPSS.

9. Steps in analysis
Step 1
The
independent
variables
which have
the
discriminati
ng power
are being
chosen
Step 2
A
discriminant
function
model is
developed by
using the
coefficients of
independent
variables.
Step 3
Wilk’s
lambda is
computed for
testing the
significance
of
discriminant
function
Step 4
The
independent
variables
which possess
importance in
discriminatin
g the groups
are being
found
Step 5
Classificatio
n of subjects
to their
respective
group is
being made

10. DA in R programming
DFA (2 groups)
library(dplyr)
library(haven)
library(ggplot2)
mydat <- read_sav("C:/Users/cpflower/Dropbox (UNC
Charlotte)/RSCH8140/R/DFA/pope.sav")
View(mydat)
scatterplotMatrix(mydat[2:4])
install.packages("DFA.data")
library(DFA.data)
DFA(data=mydat, groups="gp", variables=c('wi', 'wc', 'pc'),
predictive=TRUE, prior='SIZES', verbose=TRUE)

11. Discriminant Analysis model
The DAM involves linear combinations of the following form;
D= b₀ + b₁x₁ + b₂x₂ + b₃x₃ +….+ bĸXĸ
Where ,
D = discriminant score
b’s = discriminant coefficient / weight
x’s = predictor/ independent variable
• The coefficient / weights, are estimated so that the groups differ as much as
possible on the values of the discriminant function.
• DA– creates an equation which will minimize the possibility of misclassifying
cases into their respective groups / categories.

12. Hypothesis
• DAtests the following hypotheses;
• H₀: the group means of a set of independent variables for two /more groups
are equal.
• H₁: the group means for two/ more groups are not equal.
• Here, this group means is referred to as a centroid.

14. 1) Linear Discriminant Analysis
• Alinear combination of features
• Ronald Fishers in 1936
• This methods group images of the same classes & separates images of the
different classes.
• To identify an input test image, the projected test image is compared to each
projected training image, & the test image is identified as the closest training
image.
• This classification involving 2 target categories & 2 predictor variables.
• Images are projected from 2D spaces to C dimensional space, where C is the
no. of classes of the images.

15. How does LDA work?
Step 1:
• To calculate the seperability between
different classes also called as
between – class variance.
Step 2:
• To calculate the distance between the
mean & sample of each class, is
called the within class variance.
step 3:
• To construct the lower dimensional
space which maximizes the between
class variance & minimizes the within
class variance.

16. LDA

17. 2) Multiple Discriminant analysis
• To discriminate among more than 2 groups
• It requires g-1 no. of discriminant functions, where g is the no. of groups
• The best discriminant will be judged as per the comparison between
functions.
• Similar to multiple regression
• assumptions remain same.

18. Assumptions in DA
Assumptions:
• Apredictors are normally distributed
• The variance covariance matrices for the predictors within each of the
groups are equal.
 Sample size
 Normal distribution
 Homogenecity of variance/covariances
 Outliers
 Non- multicollinearity
 Mutually exclusive
 Classification
 Variability

19. Advantages
 Discrimination of different groups
 Accuracy of classification groups can be determined
 Helps for categorical regression analysis
 Visual graphics makes clear & understanding 2/ more categories.

20. Limitations
 LD can’t be used when subgroups are stronger.
 Predictor variables don’t strong.
 It can’t be used when there is insufficient data
 It was not usable to less no. of observation
 Small distribution gives good discriminant functions between groups.
 Large distribution gives poor discriminant functions between groups.

21. Applications
 Prediction & description DA
 Agriculture, fisheries, crop & yield studies, geoinformatics, bioinformatics, social
sciences, researches.
 Socio economics
 Hydrological & physico-chemical studies in water sources
 Face recognition
 Marketing
 Financial research
 Human resources

22. Thank you….,