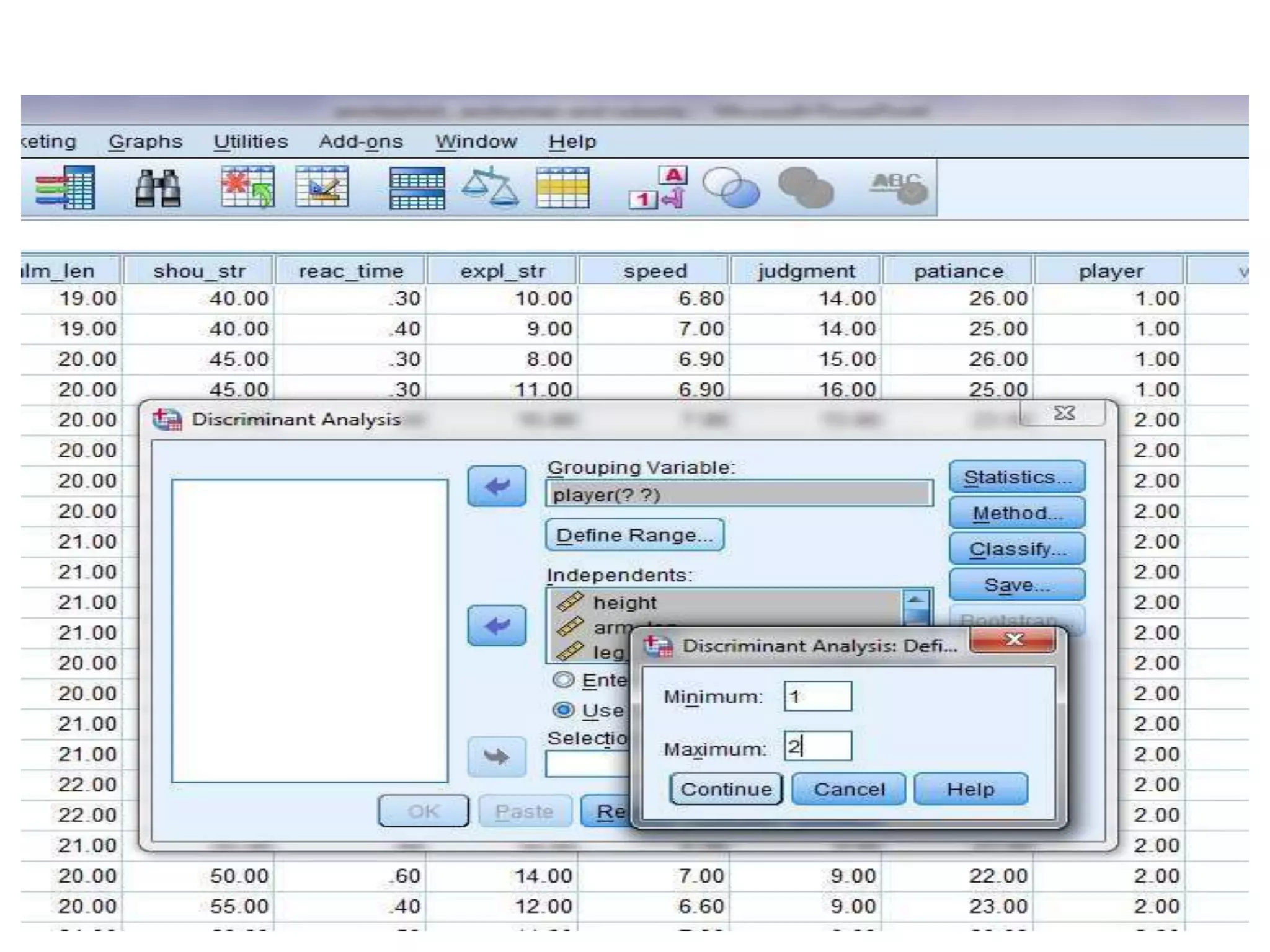
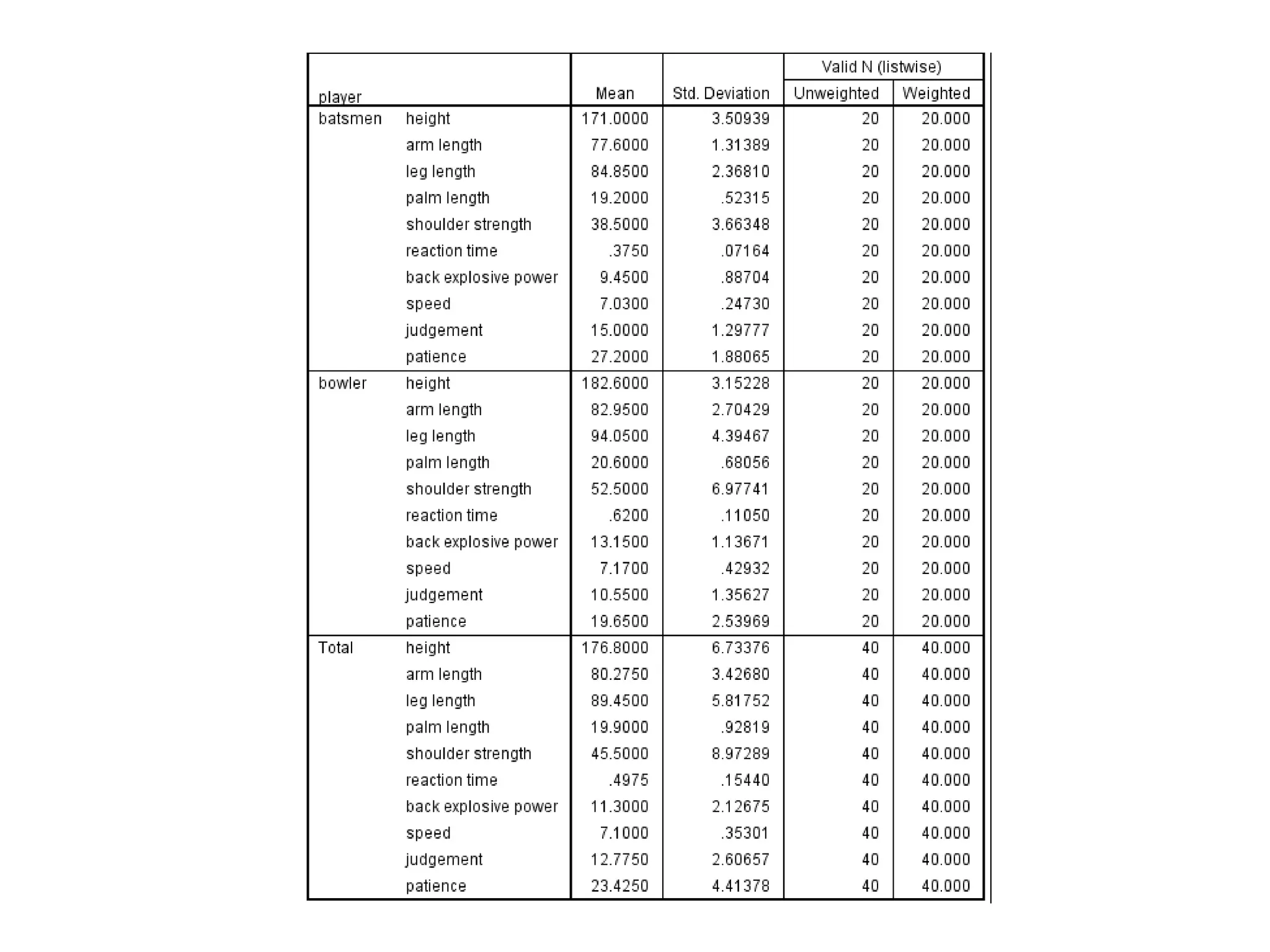
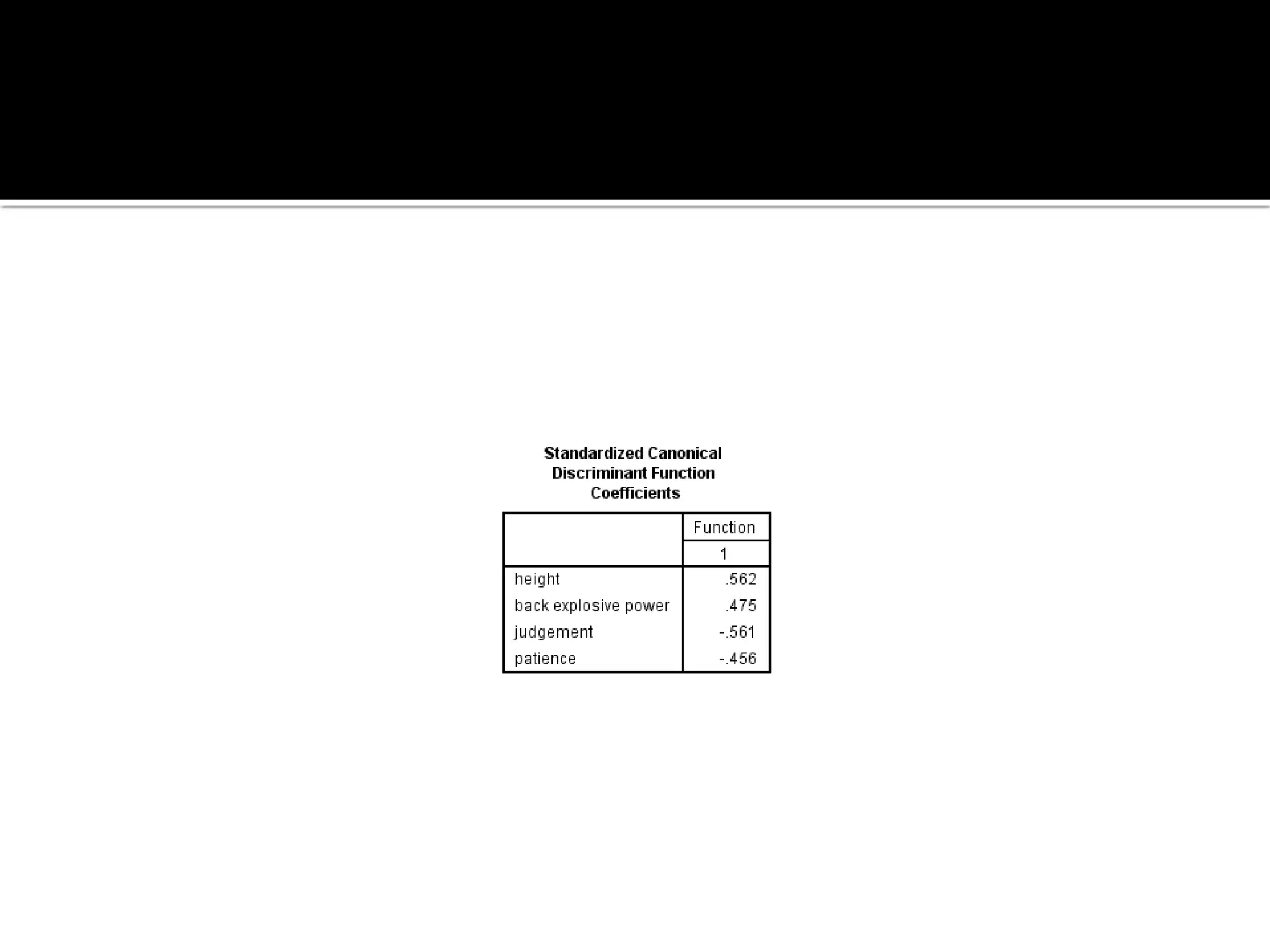
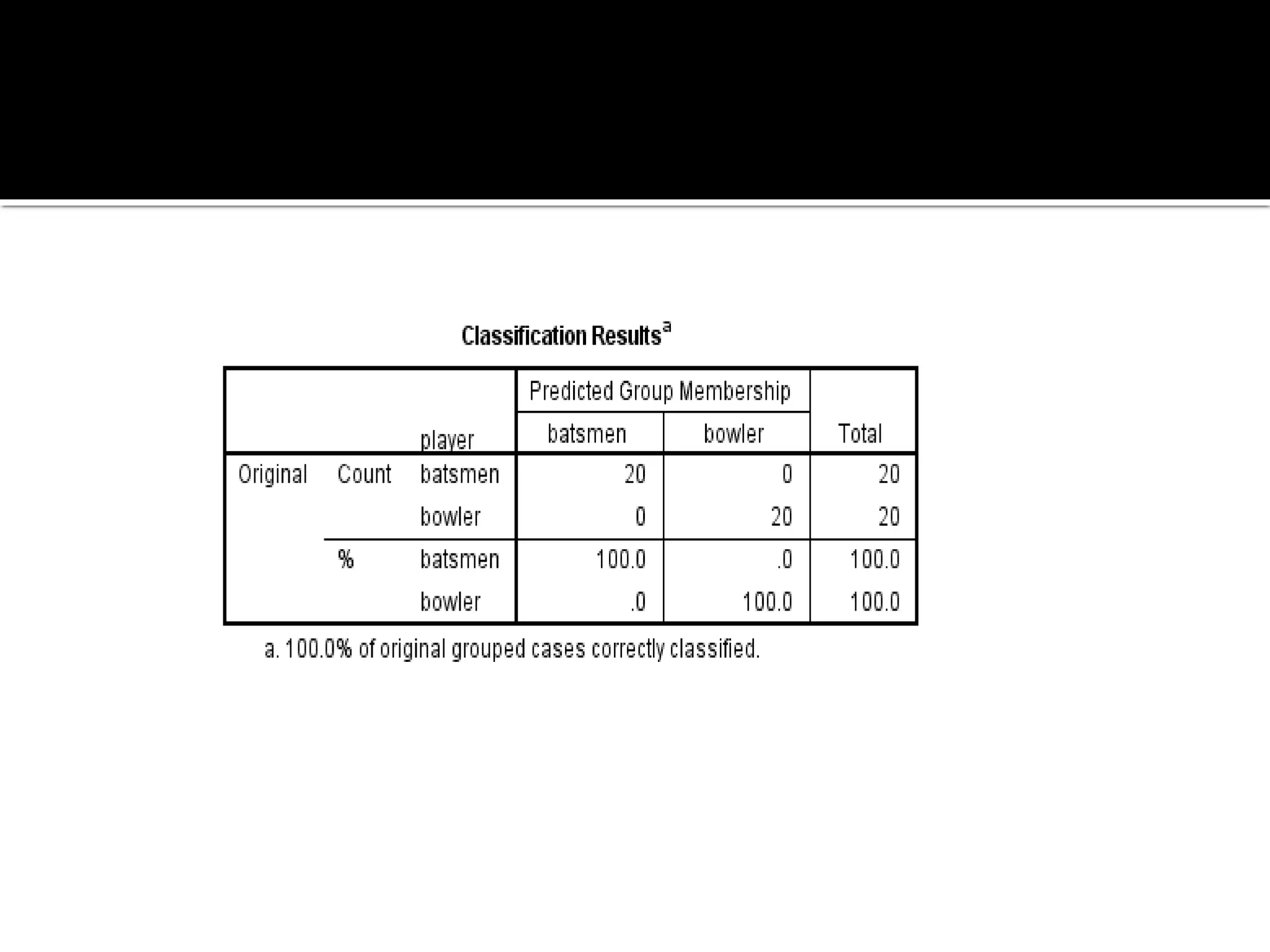
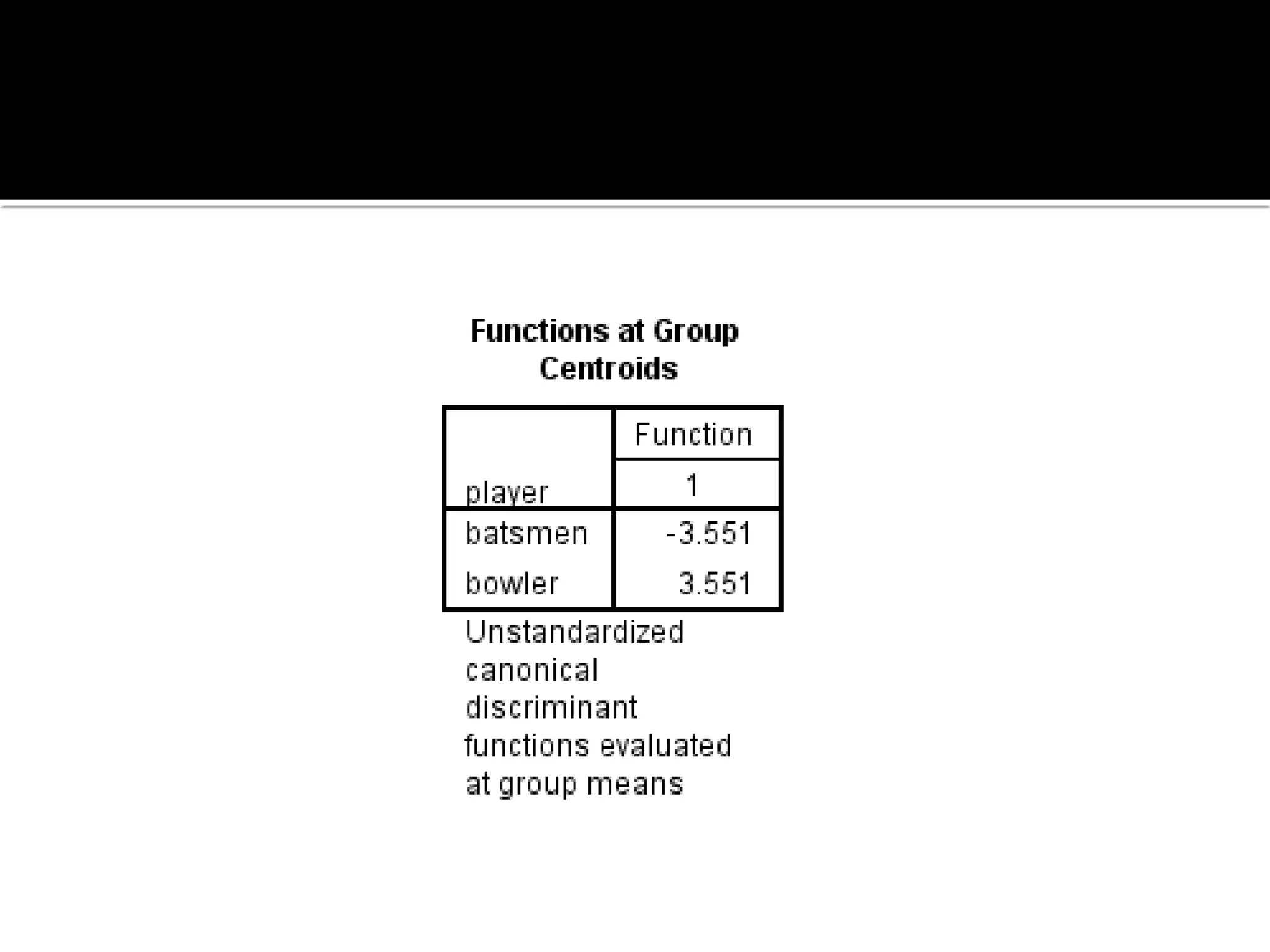
Discriminant analysis is a statistical technique used to classify individuals or cases into groups based on a set of predictor variables. It aims to determine which variables discriminate between two or more naturally occurring groups and build a model to predict group membership. The key steps involve developing discriminant functions using linear combinations of predictors, examining differences between groups on predictors, and evaluating the accuracy of classification. Discriminant analysis is commonly used to classify individuals into categories based on characteristics like athletic ability, performance level, or other attributes.

1. DISCRIMINANTANALYSIS

2.  Discriminant analysis is a classification problem,
where two or more groups or clusters or populations
are known a priori and one or more new observations
are classified into one of the known populations
based on the measured characteristics. In,
discriminant analysis, the dependent variable is a
categorical variable, whereas independent variables
are metric.
DA is sometimes also called:
 Discriminant factor analysis
 Canonical discriminant analysis

3. 1) The main purpose is to classify a subject into one of
the two groups on the basis of some independent
traits.
2) A second purpose of the discriminant analysis is to
study the relationship between group membership
and the variables used to predict the group
membership.

4.  Development of discriminant functions
 Examination of whether significant differences exist
among the groups, in terms of the predictor
variables.
 Determination of which predictor variables
contribute to most of the intergroup differences
 Evaluation of the accuracy of classification

5.  Toidentify the characteristics on the basis of which
one can classify an individual as-
1. Basket ballplayer or volleyball player on the basis
of anthropometric variables.
2. High or low performer on the basis of skill.
3. Juniors or seniors category on the basis of the
maturity parameters.

6. 1. Sample size
 group sizes of the dependent should not be grossly
different i.e. 80:20, here logistic regression may be
prefer.
 should be at least five times the number of
independent variables.
2. Normal distribution
 Each of the independent variable is normally
distributed.

7. 3. Homogeneity of variances / covariance
 All variables have linear relationships.
4.Outliers
 Outliers should not be present in the data. DA is
highly sensitive to the inclusion of outliers.
5. Mutually exclusive
 The groups must be mutually exclusive, with every
subject or case belonging to only one group.

8. 6.Classification
 Each of the allocations for the dependent categories
in the initial classification are correctly classified.
7.Variability
 No independent variables should have a zero
variability in either of the groups formed by the
dependent variable.

9. 1) Variables in the analysis are the independententities.
2) Discriminant function
 A discriminant function is a latent variable which is
constructed as a linear combination of independent
variables, such that
 Z= c+b1X1+ b2X2+…+bnXn
 The discriminant function is also known as canonical
root. This discriminant function is used to classify the
subject/cases into one of the two groups on the basis
of the observed values of the predictorvariables

10.  3) Classification matrix
 In DA, it serves as a yardstick in measuring the
accuracy of a model in classifying an individual /case
into one of the two groups. It is also known as
confusion matrix, assignment matrix, or prediction
matrix. It tells us as to what percentage of the
existing data points are correctly classified by the
model developed in DA.
 4) Stepwise method of discriminant analysis
 Discriminant function can be developed either by
entering all independent variables together or in
stepwise depending upon whether the study is
confirmatory or exploratory.

11.  5) Power of discriminatory variables
 After developing the model in the discriminant
analysis based on the selected independent
variables, it is important to know the relative
importance of the variables so selected.
 6) Box’s MTest
 By using Box’s MTests, we test a null hypothesis
that the covariance matrices do not differ between
groups formed by the dependent variable. If the
Box’s MTest is insignificant, it indicates that the
assumptions required for DA holds true.
 7) Eigen values
 Eigen value is the index of overall fit.

12.  8)WILKSlambda
 It measures the efficiency of discriminant function
in the model.
 Its value shows, how much percentage of variability
in dependent variable is not explained by the
independent variables.

 9) Cannonial correlation
 The canonical correlation is the multiple correlation
between the predictors and the discriminant
function.With only one function it provides an index
of overall model fit which is interpreted as being the
proportion of variance explained.

13.  STEP1.
In step one the
independent
variables which
have the
discriminating
power are being
chosen.
 STEP2.
A discriminant
function model is
developed by
using the
coefficients of
independent
variables

14.  STEP3.
In step three Wilk’s
lambda is computed for
testing the significance
of discriminant function.
 STEP4.
In step four the
independent variables
which possess importance
in discriminating the
groups are being found.

15. EXAMPLE USINGSPSS

16.  QUESTION - TO IDENTIFYA PLAYER INTO
DIFFERENTCATAGORIES DURINGTHE
SELECTION PROCESS INA CRICKETTRAINING
CAMP

23. OUTPUT FOR SPSS

27. 𝑋1 Height
𝑋2 Back explosive power
𝑋3 Judgement
𝑋4 Patience
Z= -24.880 + .169 × 𝑿𝟏+ .466× 𝑿𝟐- .423 × 𝑿𝟑- .204 × 𝑿𝟒

32. QUESTIONS!!!!!!!!?