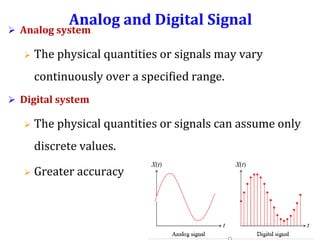
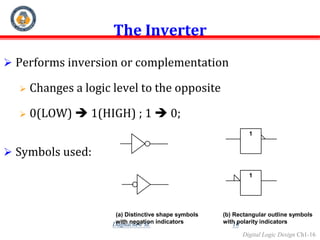
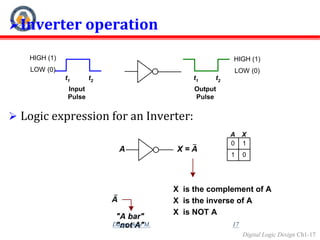
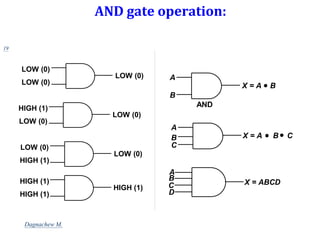
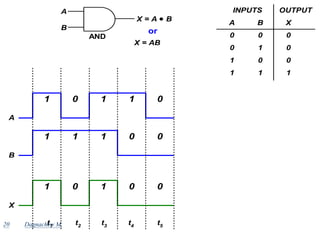
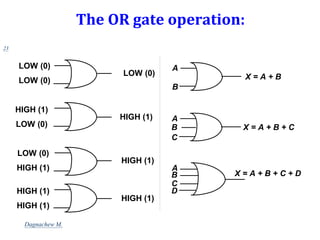
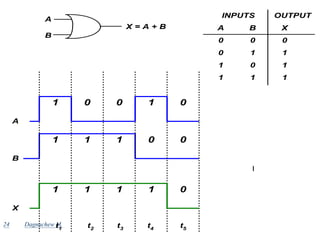
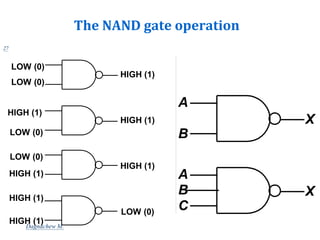
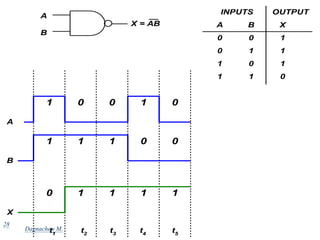
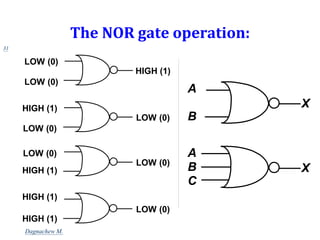
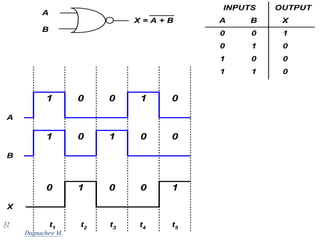
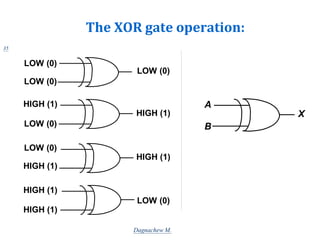
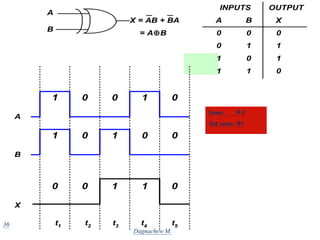
Digital systems use discrete binary values represented as 0s and 1s to process information. Common digital systems include computers, cameras, calculators, televisions and more. Analog systems represent information as continuously variable physical quantities, while digital systems represent information as discrete values. Binary digits (bits) are the fundamental units of digital systems and can have values of 0, 1, low, high, on or off. Logic gates like AND, OR, NOT, NAND and NOR are basic building blocks used to perform operations on binary inputs and produce binary outputs.

1. Digital Systems and Binary Numbers
by
Dagnachew .M
Digital Logic Design

2. Digital Systems and Binary Numbers
 Digital computers
 General purposes
 Many scientific, industrial and commercial applications
 Digital systems
 Telephone switching exchanges
 Digital camera
 Electronic calculators,
 Digital TV
 Discrete information-processing systems
 Manipulate discrete elements of information

3. Analog and Digital Signal
 Analog system
 The physical quantities or signals may vary
continuously over a specified range.
 Digital system
 The physical quantities or signals can assume only
discrete values.
 Greater accuracy
t

4. Binary Digital Signal
 Binary values are represented abstractly by:
 Digits 0 and 1
 Words (symbols) False (F) and True (T)
 Words (symbols) Low (L) and High (H)
 And words On and Off
 Binary values are represented by values
or ranges of values of physical quantities.
t
V(t)
Binary digital signal
Logic 1
Logic 0
undefine

5. Decimal Number System
 Base (also called radix) = 10
 10 digits { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }
 Digit Position
 Integer & fraction
 Digit Weight
 Weight = (Base)
Position
 Magnitude
 Sum of “Digit x Weight”
1 0 -1
2 -2
5 1 2 7 4
10 1 0.1
100 0.01
500 10 2 0.7 0.04
d2*B2
+d1*B1
+d0*B0
+d-1*B-1
+d-2*B-2
(512.74)10

6. Octal Number System
 Base = 8
 8 digits { 0, 1, 2, 3, 4, 5, 6, 7 }
 Weights
 Weight = (Base)
Position
 Magnitude
 Sum of “Digit x Weight”
 Formal Notation

7. Binary Number System
 Base = 2
 2 digits { 0, 1 }, called binary digits or “bits”
 Weights
 Weight = (Base)
Position
 Magnitude
 Sum of “Bit x Weight”
 Formal Notation
 Groups of bits 4 bits = Nibble
8 bits = Byte
1 0 -1
2 -2
2 1 1/2
4 1/4
1 0 1 0 1
1 *22
+0 *21
+1 *20
+0 *2-1
+1 *2-
=(5.25)10
(101.01)2
1 0 1 1
1 1 0 0 0 1 0 1

8. Hexadecimal Number System
 Base = 16
 16 digits { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F }
 Weights
 Weight = (Base)
Position
 Magnitude
 Sum of “Digit x Weight”
 Formal Notation
1 0 -1
2 -2
16 1 1/16
256 1/256
1 E 5 7 A
1 *162
+14 *161
+5 *160
+7 *16-1
+10 *16-2
=(485.4765625)10
(1E5.7A)16

9. The Power of 2
n 2n
0 20=1
1 21=2
2 22=4
3 23=8
4 24=16
5 25=32
6 26=64
7 27=128
n 2n
8 28=256
9 29=512
10 210=1024
11 211=2048
12 212=4096
20 220=1M
30 230=1G
40 240=1T
Mega
Giga
Tera
Kilo

10. Number Base Conversions
Decimal
(Base 10)
Octal
(Base 8)
Binary
(Base 2)
Hexadecimal
(Base 16)
Evaluate
Magnitude
Evaluate
Magnitude
Evaluate
Magnitude

11. Complements
 1’s Complement
 All ‘0’s become ‘1’s
 All ‘1’s become ‘0’s
Example (10110000)2
 (01001111)2
If you add a number and its 1’s complement …
1 0 1 1 0 0 0 0
+ 0 1 0 0 1 1 1 1
1 1 1 1 1 1 1 1

12. Complements
 2’s Complement
 Take 1’s complement then add 1
 Toggle all bits to the left of the first ‘1’ from the right
Example:
1’s Comp.:
0 1 0 1 0 0 0 0
1 0 1 1 0 0 0 0
0 1 0 0 1 1 1 1
+ 1
OR
1 0 1 1 0 0 0 0
0
0
0
0
1
0
1
0

15. Logic Gates
15
Dagnachew M.

16. Digital Logic Design Ch1-16
The Inverter
 Performs inversion or complementation
 Changes a logic level to the opposite
 0(LOW)  1(HIGH) ; 1  0;
 Symbols used:
1
1
(a) Distinctive shape symbols
with negation indicators
(b) Rectangular outline symbols
with polarity indicators
16
Dagnachew M.

17. Digital Logic Design Ch1-17
Inverter operation
 Logic expression for an Inverter:
t1
t2
t1
t2
HIGH (1)
LOW (0)
HIGH (1)
LOW (0)
Output
Pulse
Input
Pulse
A X = A
0 1
1 0
A X
X is the complement of A
X is the inverse of A
X is NOT A
A
"A bar"
"not A" 17
Dagnachew M.

18. Digital Logic Design Ch1-18
The AND Gate
 Performs ‘logical multiplication’
 If all of the input are HIGH, then the output is HIGH.
 If any of the input are LOW, then the output is LOW.
 Symbols used:
&
A
B
A
B
X
(a) Distinctive shape (b) Rectangular outline with
the AND (&) qualifying symbol
X
18
Dagnachew M.

19. AND gate operation:
LOW (0)
LOW (0)
LOW (0)
LOW (0)
HIGH (1)
LOW (0)
LOW (0)
LOW (0)
HIGH (1)
HIGH (1)
HIGH (1)
HIGH (1)
A
B
X = ABCD
C
D
A
C
B X = A B C
A
B
AND
X = A B
19
Dagnachew M.

20. 20
A B X
INPUTS OUTPUT
0 0 0
0 1 0
1 0 0
1 1 1
A
B
AND
X = A B
X = AB
or
1 1 1
0 0
A
1 1 0
1 0
B
X
1 1 0
0 0
t1
t2
t3
t4
t5
Dagnachew M.

21. Logic expressions for AND gate:
21
 AND gate performs Boolean multiplication
 Boolean multiplication follows the same basic rule as binary
multiplication:
0 . 0 = 0
0 . 1 = 0
1 . 0 = 0
1 . 1 = 1
Dagnachew M.

22. Digital Logic Design Ch1-22
The OR Gate
 Performs ‘logical addition’
 If any of the input are HIGH, then the output is HIGH.
 If all of the input are LOW, then the output is LOW
 Symbols used:
1
A
B
A
B
X
(a) Distinctive shape (b) Rectangular outline with
the OR ( 1) qualifying symbol
X
22
Dagnachew M.

23. The OR gate operation:
LOW (0)
LOW (0)
LOW (0)
HIGH (1)
HIGH (1)
LOW (0)
HIGH (1)
LOW (0)
HIGH (1)
HIGH (1)
HIGH (1)
HIGH (1)
A
B
X = A + B
A
C
X = A + B + C
B
A
C
X = A + B + C + D
B
D
23
Dagnachew M.

24. 24
A B X
INPUTS OUTPUT
0 0 0
0 1 1
1 0 1
1 1 1
A
B
X = A + B
1 0 1
0 0
A
1 1 0
1 0
B
X
1 1 1
1 0
t1
t2
t3
t4
t5
Dagnachew M.

25. Logic expressions for OR gate:
25
 OR gate performs Boolean addition
 Boolean addition follows the basic rules as follows:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 1
Dagnachew M.

26. Digital Logic Design Ch1-26
The NAND Gate
 NAND  NOT-AND combines the AND gate and an
inverter
 Used as a universal gate
 Combinations of NAND gates can be used to perform
AND, OR and inverter operations
 If all or any of the input are LOW, then the output is
HIGH.
 If all of the input are HIGH, then the output is LOW
 Symbol used: A
B
X
A
B
X
(a) Distinctive shape: 2 input NAND
gate and its NOT/AND equivalent
&
A
B
X
(b) Rectangular outline: 2 input
NAND gate with polarity indicator
26
Dagnachew M.

27. The NAND gate operation
HIGH (1)
LOW (0)
LOW (0)
HIGH (1)
HIGH (1)
LOW (0)
HIGH (1)
LOW (0)
HIGH (1)
LOW (0)
HIGH (1)
HIGH (1)
A
B
X
A
C
X
B
27
Dagnachew M.

28. 28
A B X
INPUTS OUTPUT
0 0 1
0 1 1
1 0 1
1 1 0
1 0 1
0 0
A
1 1 0
1 0
B
X
0 1 1
1 1
t1
t2
t3
t4
t5
A
B
X = AB
Dagnachew M.

29. Digital Logic Design Ch1-29
Logic expressions for NAND gate:
 Boolean expression for NAND is a combination of AND
and Inverter Boolean expressions.
A B AB
INPUTS OUTPUT
0 0 0
0 1 0
1 0 0
1 1 1
AB = X
0.0 = 0 = 1
0.1 = 0 = 1
1.0 = 0 = 1
1.1 = 1 = 0
29
Dagnachew M.

30. Digital Logic Design Ch1-30
The NOR Gate
 NOR  NOT-OR combines the OR gate and an inverter
 Used as a universal gate
 Combinations of NOR gates can be used to perform AND, OR
and inverter operations
 If all or any of the input are HIGH, then the output is LOW.
 If all of the input are LOW, then the output is HIGH
Symbol used:
(a) Distinctive shape: 2 input NOR
gate and its NOT/OR equivalent
A
B
X
1
A
B
X
(b) Rectangular outline with
the OR ( 1) qualifying symbol
A
B
X
30
Dagnachew M.

31. The NOR gate operation:
HIGH (1)
LOW (0)
LOW (0)
LOW (0)
HIGH (1)
LOW (0)
LOW (0)
LOW (0)
HIGH (1)
LOW (0)
HIGH (1)
HIGH (1)
A
B
X
A
C
X
B
31
Dagnachew M.

32. 32
A B X
INPUTS OUTPUT
0 0 1
0 1 0
1 0 0
1 1 0
A
B
X = A + B
1 0 1
0 0
A
1 1 0
0 0
B
X
0 0 0
1 1
t1
t2
t3
t4
t5
Dagnachew M.

33. Digital Logic Design Ch1-33
Logic expressions for NOR gate:
 Boolean expression for NOR is a combination of OR
and Inverter Boolean expressions.
A B A + B
INPUTS OUTPUT
0 0 0
0 1 1
1 0 1
1 1 1
A + B = X
0+0 = 0 = 1
0+1 = 1 = 0
1+0 = 1 = 0
1+1 = 1 = 0
33
Dagnachew M.

34. Digital Logic Design Ch1-34
The Exclusive-OR gate
 Combines basic logic circuits of AND, OR and Inverter. Has only 2 inputs
 Used as a universal gate
 Can be connected to form an adder that allows a computer to do perform
addition, subtraction, multiplication and division in ALU
 If both of the input are at the same logic level, then the output is LOW.
 If both of the input are at opposite logic levels, then the output is HIGH
Symbol used:
(a) Distinctive shape
A
B
X
= 1
A
B
X
(b) Rectangular outline
34
Dagnachew M.

35. The XOR gate operation:
LOW (0)
LOW (0)
LOW (0)
HIGH (1)
HIGH (1)
LOW (0)
HIGH (1)
LOW (0)
HIGH (1)
LOW (0)
HIGH (1)
HIGH (1)
A
B
X
35
Dagnachew M.

36. 36
A B X
INPUTS OUTPUT
0 0 0
0 1 1
1 0 1
1 1 0
A
B
X = AB + BA
= A B
1 0 1
0 0
A
1 1 0
0 0
B
X
0 1 1
0 0
t1
t2
t3
t4
t5
Sama  0
Tak sama 1
Dagnachew M.

37. Digital Logic Design Ch1-37
The Exclusive-NOR gate
 Has only 2 inputs, but output of XNOR is the opposite of XOR
 If both of the input are at the same logic level, then the output
is HIGH.
 If both of the input are at opposite logic levels, then the
output is LOW.
Symbol used:
(a) Distinctive shape
A
B
X
= 1
A
B
X
(b) Rectangular outline
37
Dagnachew M.

38. The XNOR gate operation:
A
B
X
38
LOW (1)
LOW (0)
LOW (0)
HIGH (0)
HIGH (1)
LOW (0)
HIGH (0)
LOW (0)
HIGH (1)
LOW (1)
HIGH (1)
HIGH (1)
Dagnachew M.

39. 39
A B X
INPUTS OUTPUT
0 0 1
0 1 0
1 0 0
1 1 1
A
B
X = A B
1 0 1
0 0
A
1 1 0
0 0
B
X
1 0 0
1 1
t1
t2
t3
t4
t5
Dagnachew M.

40. XOR vs XNOR
40
1 0 1
0 0
A
1 1 0
0 0
B
XOR
0 1 1
0 0
t1
t2
t3
t4
t5
1 0 0
1 1
XNOR
Dagnachew M.