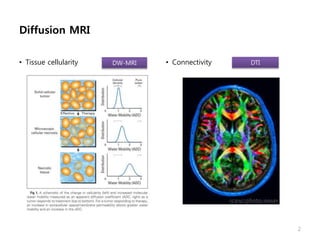
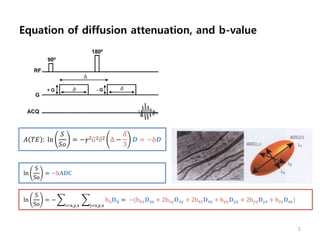
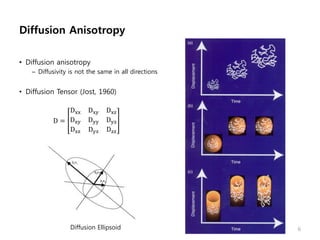
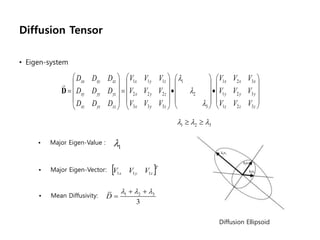
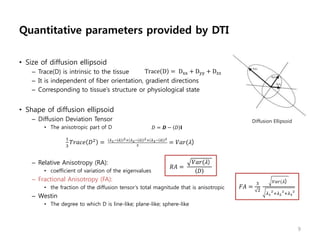
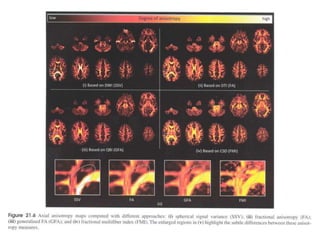
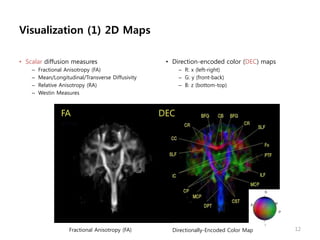
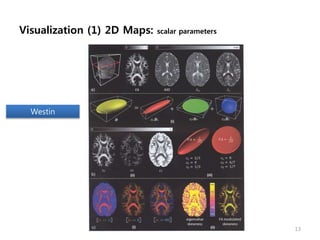
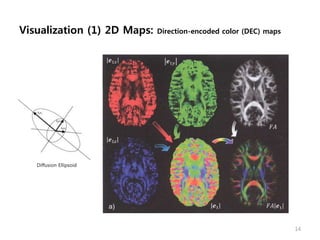
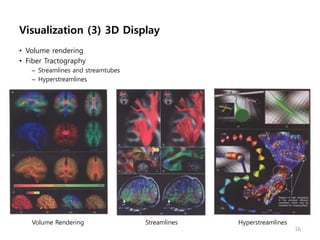
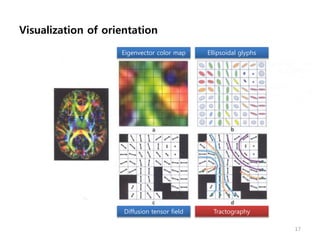
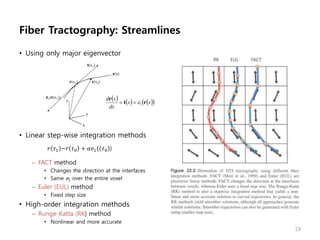
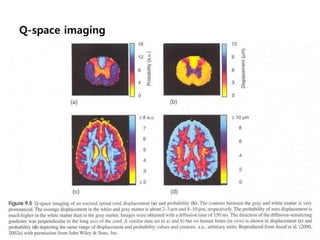
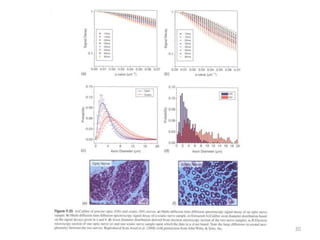
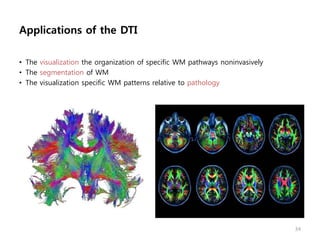
This document provides an overview of diffusion tensor imaging (DTI). It describes how DTI can be used to measure the diffusion of water molecules in tissue to determine tissue cellularity and connectivity. Key aspects covered include diffusion anisotropy, the diffusion tensor, quantitative DTI parameters like fractional anisotropy, visualization techniques like fiber tractography, limitations of DTI like issues with crossing fibers, and more advanced methods like probabilistic fiber tracking and high b-value q-space imaging.

1. Diffusion Tensor Imaging
2011. 10. 4.
KAIST 바이오및뇌공학과
이정원
1

2. Diffusion MRI
• Tissue cellularity • Connectivity
2
DW-MRI DTI

3. Outline
• Diffusion Anisotropy
• Diffusion Tensor
• Quantitative parameters from Diffusion Tensor
• Visualization
• Fiber Tracking
• Probabilistic Fiber Tracking
• High b-value q-space imaging
3

4. What is diffusion?
• Einstein recognized that Brownian motion was associated with diffusion
– No macroscopic concentration gradient is needed.
– Self-diffusion arising from local concentration fluctuations
• Einstein derived the self-diffusion coefficient of the Brownian particle
– Einstein expressed the energy change as the total work done by the particles contained within
the volume
– Diffusion coefficient
• Einstein rewrote Fick’s laws for the diffusion
– in terms of diffusion under probability gradients
𝐷 =
𝑘 𝐵 𝑇
6𝜋𝜂𝑅
: Sutherland-Einstein relation (1905)
𝑘 𝐵 ∶ 𝐵𝑜𝑙𝑡𝑧𝑚𝑎𝑛𝑛′
𝑠 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡
𝜂 ∶ viscosity
T ∶ absolute temperature
R ∶ radius of the spherical particle
𝐾𝑛
𝜁
− 𝐷
𝛿𝑛
𝛿𝑥
= 0
𝐾 ∶ 𝑛𝑒𝑡 𝑓𝑜𝑟𝑐𝑒
𝑛 ∶ the number of Brownian particles per unit volume
𝜁 ∶ friction
D ∶ diffusion coefficient
X ∶ position
𝑃 𝑟 𝑟′
, 𝑡 : 𝑐𝑜𝑛𝑑𝑖𝑡𝑖𝑜𝑛𝑎𝑙 𝑝𝑟𝑜𝑏𝑎𝑏𝑙𝑖𝑡𝑦 𝑡ℎ𝑎𝑡 𝑎 𝑝𝑎𝑟𝑡𝑖𝑐𝑙𝑒 𝑠𝑡𝑎𝑟𝑡𝑖𝑛𝑔 𝑎𝑡 𝑟 𝑎𝑡 𝑡𝑖𝑚𝑒 𝑧𝑒𝑟𝑜 𝑤𝑖𝑙𝑙 𝑚𝑜𝑣𝑒 𝑡𝑜 𝑟′
𝑎𝑓𝑡𝑒𝑟 𝑎 𝑡𝑖𝑚𝑒 𝑡
: Einstein equation for diffusion
4

5. Equation of diffusion attenuation, and b-value
𝐴 𝑇𝐸 : ln
𝑆
𝑆𝑜
= −𝛾2 𝐺2 𝛿2 ∆ −
𝛿
3
𝑫 = −𝑏𝑫
5
ln
S
So
= −b𝐀𝐃𝐂
ln
S
So
= −
i=x,y,z
.
j=x,y,z
bij 𝐃𝐢𝐣 = −(bxx 𝐃 𝐱𝐱 + 2bxy 𝐃 𝐱𝐲 + 2bxz 𝐃 𝐱𝐳 + byy 𝐃 𝐲𝐲 + 2byz 𝐃 𝐲𝐳 + bzz 𝐃 𝐳𝐳)

6. Diffusion Anisotropy
• Diffusion anisotropy
– Diffusivity is not the same in all directions
• Diffusion Tensor (Jost, 1960)
6
D =
Dxx Dxy Dxz
Dxy Dyy Dyz
Dxz Dyz Dzz
Diffusion Ellipsoid

7. How to measure the components of Diffusion Tensor
• DTI needs more than 7 DW-MRIs
7
D =
Dxx Dxy Dxz
Dxy Dyy Dyz
Dxz Dyz Dzz

8. 











































zzz
yyy
xxx
zyx
zyx
zyx
zzyzxz
yzyyxy
xzxyxx
VVV
VVV
VVV
VVV
VVV
VVV
DDD
DDD
DDD
321
321
321
3
2
1
333
222
111



D

321  
Diffusion Tensor
• Major Eigen-Value :
• Major Eigen-Vector:
1
 T
zyx VVV 111
• Mean Diffusivity: 1 2 3
3
D
   

Diffusion Ellipsoid
• Eigen-system

9. Diffusion Ellipsoid
Quantitative parameters provided by DTI
• Size of diffusion ellipsoid
– Trace(D) is intrinsic to the tissue
– It is independent of fiber orientation, gradient directions
– Corresponding to tissue’s structure or physiological state
• Shape of diffusion ellipsoid
– Diffusion Deviation Tensor
• The anisotropic part of D
– Relative Anisotropy (RA):
• coefficient of variation of the eigenvalues
– Fractional Anisotropy (FA):
• the fraction of the diffusion tensor’s total magnitude that is anisotropic
– Westin
• The degree to which D is line-like; plane-like; sphere-like
9
Trace D = Dxx + Dyy + Dzz
𝑅𝐴 =
𝑉𝑎𝑟(𝜆)
𝐷
𝐹𝐴 =
3
2
𝑉𝑎𝑟(𝜆)
𝜆1
2
+𝜆2
2
+𝜆3
2
𝐷 = 𝑫 − 𝐷 𝐈
1
3
𝑇𝑟𝑎𝑐𝑒 𝐷2
= 𝜆1− 𝜆 2+ 𝜆2− 𝜆 2+ 𝜆3− 𝜆 2
3
= 𝑉𝑎𝑟(𝜆)

10. 10

11. The two main challenges with DTI
11
Visualization Fiber Tracking

12. Visualization (1) 2D Maps
• Scalar diffusion measures
– Fractional Anisotropy (FA)
– Mean/Longitudinal/Transverse Diffusivity
– Relative Anisotropy (RA)
– Westin Measures
• Direction-encoded color (DEC) maps
– R: x (left-right)
– G: y (front-back)
– B: z (bottom-top)
12Fractional Anisotropy (FA) Directionally-Encoded Color Map
FA DEC

13. Visualization (1) 2D Maps: scalar parameters
13
Westin

14. Visualization (1) 2D Maps: Direction-encoded color (DEC) maps
14
Diffusion Ellipsoid

15. Visualization (2) Glyph Representations
15

16. Visualization (3) 3D Display
• Volume rendering
• Fiber Tractography
– Streamlines and streamtubes
– Hyperstreamlines
16
HyperstreamlinesVolume Rendering Streamlines

17. Visualization of orientation
17
Eigenvector color map Ellipsoidal glyphs
Diffusion tensor field Tractography

18. Fiber Tractography
• Fiber Tracking
– The reconstruction of long neuronal fibers from the information about anisotropic diffusion
– In vivo and noninvasively
• Methods
– Streamlines
• FACT (Fiber Assignment by Continuous Tracking)
• Euler (EUL)
• Runge-Kutta (RK)
– Tensor Deflection
• TEND (Tensor Deflection)
• Tensorlines
– Other variations
• G-TRACT
• Gibbs tracking algorithm
18

19. Fiber Tractography: Streamlines
• Using only major eigenvector
• Linear step-wise integration methods
– FACT method
• Changes the direction at the interfaces
• Same e1 over the entire voxel
– Euler (EUL) method
• Fixed step size
• High-order integration methods
– Runge-Katta (RK) method
• Nonlinear and more accurate
19
𝑟 𝜏1 ~𝑟 𝜏0 + 𝛼𝑒1( 𝜏0 )
      ss
ds
sd
rt
r
1

20. Fiber Tractography: Seeding and Stopping Criteria
• Seed location
– Regional seed methods
• To extract a specific pathway or mapping tracts from a specific region
– Whole-brain seed methods
• To generate nearly al possible pathways
• Higher redundancy in the pathways
• Stopping Criteria
– FA threshold
– Curvature Criteria
20

21. Limitations of DTI
• Tract Dispersion
– The variance or uncertainty in tractography results
– Tract dispersion increases as the SNR is decreased
• Tract Deviation
– Systematic errors in the tract position
– Tract deviation is influenced by the step size
• Tract Divergence and Convergence
– Local heterogeneity of the diffusion tensor field
• Crossing Fibers
21

22. Strong diffusion weighting with Crossing Fibers
22

23. Diffusion Circular Spectrum Imaging
• Case 1: Single Fiber
W.Zhan et. al. MRM 2003, 49:1077

24. Diffusion Circular Spectrum Imaging
• Case 2: Fiber-Crossing
W.Zhan et. al. MRM 2003, 49:1077

25. HARDI (high angular resolution DW imaging) acquisition
25

26. Q-space Imaging
• High b-value q-space analysis
– Signal decay is not monoexponential at high b-value (>10000 s/mm2) DW-MRI
– Reflect a smaller structure information in stronger gradient or longer diffusion time
– To emphasizes the diffusion characteristics of the slow-diffusing component
– Extremely useful for detection restricted diffusion (Assaf et al., MRM, 2002)
• Q-space analysis
26

27. Displacement in PGSE with short/long gradient pulses
27

28. Displacement and probability maps from DWI
28

29. Q-space imaging
29

30. 30

31. Probabilistic Fiber Tracking
• A limitation of deterministic tractography
– The lack of information regarding the error in the tracking procedure in any given
experiment
• Probabilistic tractography methods
– To explicit characterization of the confidence with which connections may be established
through the diffusion MRI
– Uses probability density functions (PDFs) of fiber orientation
• To capture the expected distribution of possible fiber orientations
– Is effective at identifying multiple possible routes for connections from the chosen single
start point
• Advantages
– Better accounts for experimental errors
– More robust tracking results
– Better deals with crossing fibers, low SNR
• Disadvantages
– Computationally intense
– Probabilities will be modified by crossing fibers
31

32. Probabilistic Fiber Tracking
• Methods
– Monte Carlo Streamlines
• Simulation the rage of possible outputs of a deterministic tracking process
• Random sampling of the PDF
• At least 1000 samples for each voxel’s PDF
– Simulated Diffusion Random Walk
• To invoke the diffusion process itself as a propagator for the tractography process
• generate PDFs on the basis of measures derived from the diffusion orientation distribution function
• Each jump during the random walk is typically independent of any of the previous jumps
– Front evolution methods
• The evolution of the front is deterministic rather than statistical
• Front evolution methods generate maps of a distributed ‘degree of connection’ index (fast marching
tractography)
32

33. Deterministic- vs. Probabilistic Tractography
33
Tournier, J.-D., Mori, S., and Leemans, A. (2011). “Diffusion tensor imaging and beyond.”
Magnetic resonance in medicine : official journal of the Society of Magnetic Resonance
in Medicine / Society of Magnetic Resonance in Medicine, 65(6), pp. 1532-56.

34. Applications of the DTI
• The visualization the organization of specific WM pathways noninvasively
• The segmentation of WM
• The visualization specific WM patterns relative to pathology
34

35. Limitations of the DTI
1. It is not possible to differentiate afferent from efferent pathways, anterograde and
retrograde pathways, inhibitory and excitatory connections, and direct versus
indirect route in diffusion data
2. Tractography picks up mainly large-fiber pathways; smaller pathways, or those
through regions of fiber crossing of interrupted by synapses may not be detected
3. The probability of tracing a pathway between two points will be influenced by
factors other than the true existence of an anatomical connection – for example,
longer or more tortuous paths are less likely to be traced
35

36. References
36
[1] Tournier, J.-D., Mori, S., and Leemans, A. (2011).
“Diffusion tensor imaging and beyond.” Magnetic
resonance in medicine : official journal of the Society
of Magnetic Resonance in Medicine / Society of
Magnetic Resonance in Medicine, 65(6), pp. 1532-56.
[2] Callaghan, P., Codd, S., and Seymour, J. (1999).
“Spatial coherence phenomena arising from
translational spin motion in gradient spin echo
experiments.” Concepts in Magnetic Resonance, 11(4),
pp. 181–202.
[3] Cohen, Y. and Assaf, Y. (2002). “High b-value q-
space analyzed diffusion-weighted MRS and MRI in
neuronal tissues - a technical review.” NMR in
biomedicine, 15(7-8), pp. 516-42.