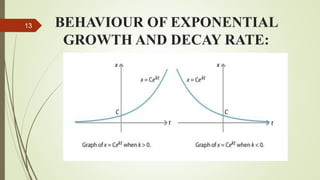
This document discusses differential equations and their applications. It defines ordinary and partial differential equations, and describes various types of ordinary differential equations including separable, homogeneous, non-homogeneous, exact, and linear equations. It also discusses exponential growth and decay models using differential equations. Examples are provided to illustrate radioactive decay modeling using half-life equations and carbon dating to determine the age of fossils.

1. 1

2. Differential Equation
DEFINITION
 An equation containing the derivatives of one or more
dependent variables, with respect to one or more independent
variables, is said to be a differential equation (DE).
Classification by type
 Ordinary Differential Equations (ODE)
 Partial Differential Equations (PDE)
2

3.  Ordinary Differential Equations (ODE)
 Contains one or more dependent variables
 with respect to one independent variable
Classification by type
𝑑𝑦
𝑑𝑥
→ 𝑦′
3

4. Partial Differential Equations (PDE)
 involve one or more dependent variables
 and two or more independent variables
First Order Ordinary Differential Equations (ODE)
Types of first order ODE
• Separable equation
• Homogenous equation
• Non Homogeneous equation
• Exact equation
• Linear equation
4

5. Separable Equation5

6. 6

7. Radioactivity
The spontaneous decay of certain unstable atomic nuclei
7

8. Half- life
The time required for one half of the atoms of a
radioactive substance to decay
8

9. Half-life equation:9

10. EXPONENTIAL GROWTH
AND DECAY RATE:
10

11. Exponential growth(k):
Is a phenomenon that occurs when the growth rate of the value of a
mathematical function is proportional to the function's current value, resulting
in its growth with time being an exponentialfunction.
Exponential decay(k):
Occurs in the same way when the growth rate is negative.
11

12. Equation of Growth & Decay Rate
The general equation is given as:
yꞌ=k y or y(t)= 𝒚 𝟎
Where “k” is the(exponential growth or decay)constant.
When value of k is positive means k>0,then it is growth rate
constant.
When value of k is negative means k<0,then it is decay rate
constant.
𝒆 𝒌𝒕
12

13. BEHAVIOUR OF EXPONENTIAL
GROWTH AND DECAY RATE:
13

14. PROOF OF EQUATION:
yꞌ = ky
So, all solutions of yꞌ = ky are in the form of y = Cekt which is a general solution of above
equation.
Seperating variables:
𝒚′
𝒚
=k
𝑦′
𝑦
dt = 𝑘 𝑑𝑡
𝒅𝒚
𝒅𝒕
= 𝒚′
𝟏
𝒚
𝒅𝒚 = 𝒌 𝒅𝒕
𝐥𝐧 𝒚 = 𝒌𝒕 + 𝑪
𝒚 = 𝒆 𝒌𝒕
𝒆 𝑪
𝒚 = 𝑪𝒆 𝒌𝒕
14

15. EXAMPLE:
A colony of bacteria is grown under ideal conditions in a laboratory so that the
population increases exponentially with time. At the end of 3 hours there are
10,000 bacteria. At the end of 5 hours there are 40,000. How many bacteria
were present initially?
SOLUTION:
y(t)=𝒚 𝟎 𝑒 𝑘 𝑡
We have given;
t=3 hours
10, 000 = 𝒚 𝟎 𝒆 𝟑𝒌 1
t=5 hours
40, 000 = 𝑦𝑜 𝑒5𝑘
2
Dividing the second by first to get :
4 = 𝑒2𝑘
15

16. Taking natural log on both sides to eliminate exponential:
2k = ln 4
k = ln 2.
Now we have to put the value of “k” in above equation:
10, 000 = 𝑦0 𝑒 𝑙𝑛23
= 𝑦08
𝑦0= 10,000/8
𝑦0=1250
Result :
So, 1250 bacteria are present initially.
16

17. Example 2
A herd of llamas has 1000 llamas in it, and the
population is growing exponentially. At time t=4 it
has 2000 llamas. Write a formula for the number of
llamas at arbitrary time t.
17

18.  SOLUTION:
The differential equation of exponentially growth will be :18

19. Example 3
 Use the fact that the world population was 2560 million people
in 1950 and 3040 million in 1960 to model the population of the
world in the second half of the 20th century. (Assume that the
growth rate is proportional to the population size.) What is the
relative growth rate k? Use the model to estimate the world
population in 1993 and to predict the population in the year
2020.
 SOLUTION:
19

20. 20

21. Carbon dating
Carbon-14 dating to determine the age of fossil remains
 Determine the age of fossils up to about 50,000year old.
 It is used in dating things such as:
 bone
 cloth
 wood
 plant
 fibers
 Radioactive isotope of carbon have a relatively long half-life
(5700 years).
21

22. Decay of radioactive isotopes
Radioactive isotopes, such as decay exponentially. The half-life of an isotope is
defined as the amount of time it takes for there to be half the initial amount of the
radioactive isotope present.
For example
Suppose you have N0 grams of a radioactive isotope that has a half-life of t* years. Then we
know that after one half-life (or t* years later), you will have
1
2
𝑁0=
𝑁0
2
grams of that isotopes
t* years after that (i.e. 2t* years from the initial measurement), there will be
(
1
2
)(
1
2
) 𝑁0=
𝑁0
4
grams.
3t* years after the initial measurement there will be
(
1
2
)(
1
2
)(
1
2
) 𝑁0=
𝑁0
8
grams.
and so on…
22

23. General equation for exponential decay
N (t) = N0e kt .
Returning to our example of carbon, knowing that the half-life of 14C is 5700 years, we can
use this to find the constant, k. That is when t = 5700, there is half the initial amount of 14C.
 Initial amount of 14C is the amount of 14C when t = 0,
or N0 (i.e. N(0) = N0e k⋅0 = N0e0 = N0). Thus, we can write:
Simplifying this expression by canceling the N0 on both sides of the equation gives,
Solving for the unknown, k, we take the natural logarithm of both sides,
23

24. Thus, our equation for modeling the decay of 14C is given by,24

25. Radiocarbon dating
The half-lives of several radioactive isotopes are known
and are used often to figure out the age of newly found
fossils.
 Different isotopes have different half-lives and
sometimes more than one present isotope can be used
to get an even more specific age of a fossil.
25

26. EXAMPLE: A fossil contains 25% of the original amount of C14 ® how
old is it?
Remember: At time zero the amount was 100% and then they began to
decay –Now there are only 25% left over.
Phys. Facts: Half-life of 14C=5730 years
our differential equation using separation of variables as
What is left is to determine the value of k.
For that we use the knowledge that after 5730 years
the amount of has decayed to ½ of the original amount:
26

27. It shouldn’t surprise us that k turns out being very small and negative – after all
the number of is decreasing and it is doing this at a relatively slow rate!
So, for our fossil:
27

28. Since we know now the exact law for decay, we are able
to determine the age of the fossil immediately. 11,460
years, this is quite some age.
28

29. Conclusion
HALF LIFE IS THE AMOUNT OF TIME IT TAKES
FOR ONE HALF OF THE RADIOACTIVE
MATERIAL TO DECAY INTO A STABLE FORM.
BEFORE DECAY BEGINS, ALL OF THE
MATERIAL IS RADIOACTIVE
29

30. AFTER ONE HALF LIFE, HALF OF THE SAMPLE
REMAINS RADIOACTIVE AND THE OTHER HALF IS
STABLE
AFTER EACH ADDITIONAL HALF LIFE, HALF OF
THE REMAINING RADIOACTIVE MATERIAL
DECAYS
30

31. 31