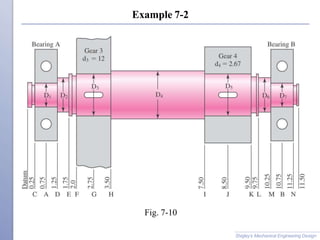
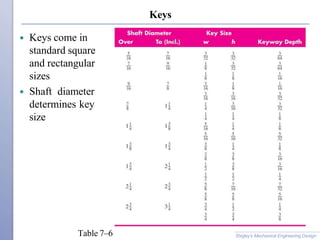
This document summarizes key considerations for designing shafts and shaft components. It discusses material selection, geometric layout, stress and strength analysis, deflection, and vibration due to natural frequency. Key steps in shaft design include considering the axial layout of components, supporting axial loads, providing for torque transmission, and enabling assembly and disassembly. Critical locations on shafts are evaluated for stress, and equations are provided to calculate stresses from bending, torsion, and combined loads. Deflection and critical speeds are also addressed. Examples demonstrate applying the summarized design methodology.