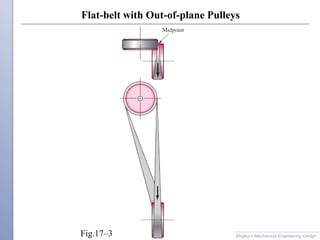
The document discusses various types of flexible drives used to transmit power between shafts, including belts, chains, ropes, and flexible shafts. It provides details on belt and chain types, characteristics, design considerations, equations, and examples. Flexible drives allow for power transmission over long distances between shafts compared to rigid couplings and can accommodate some misalignment, though they have speed and power limits compared to gears.

1. Belt and Chain Drives
(Flexible Drive Elements)
Shigley’s Mechanical Engineering Design

2. Why Flexible Drives?
Shigley’s Mechanical Engineering Design
+
• Long Distances Between Shafts
• Less Expensive
• Adjustable Centers
• Tolerates some mis alignment better than gears
-
• Not as compact as gears
• Some speed limits
• Power and torque limits

3. Common Belt Types
Shigley’s Mechanical Engineering Design
Type Pulley
1. Flat Crowned pulley
(conveyor belts)
2. Round (O-ring) Grooved pulley
3. V-belt Flanged pulleys
4. Timing (toothed) Cogged pulley
(no stretch or slip)
5. Proprietary belt designs

4. Characteristics of Some Common Belt Types
Shigley’s Mechanical Engineering Design
Table 17–1

5. Flat Belt Drive
Shigley’s Mechanical Engineering Design
Better for high speed applications,
rather than power.
Good for tight clearances
Can allow slip, to prevent breakage

6. Flat Belts as Conveyer Belts
Shigley’s Mechanical Engineering Design
Usually seamed/stitched
Crowned Pulleys for Tracking

7. O-Ring Drive
Shigley’s Mechanical Engineering Design
Good for low cost.
Good for driving multiple shafts

8. Reversing Belts
Shigley’s Mechanical Engineering Design
Fig.17–2
Typically
O-Ring
Drives

9. Timing Belts
Shigley’s Mechanical Engineering Design
Fig.17–15

10. Flat-belt with Out-of-plane Pulleys
Shigley’s Mechanical Engineering Design
Fig.17–3

11. Variable-Speed Belt Drives
Shigley’s Mechanical Engineering Design
Fig.17–5

12. Flat-Belt Geometry – Open Belt
Shigley’s Mechanical Engineering Design
Fig.17–1a

13. Free Body of Infinitesimal Element of Flat Belt
Shigley’s Mechanical Engineering Design
Fig.17–6

14. Free Body of Infinitesimal Element of Flat Belt
Shigley’s Mechanical Engineering Design
Fig.17–6

15. Analysis of Flat Belt, The Belting Equation
Shigley’s Mechanical Engineering Design
The Belting Equation

16. Fc = Hoop Tension Due to Centrifugal Force
Shigley’s Mechanical Engineering Design

17. Forces and Torques on a Pulley
Shigley’s Mechanical Engineering Design
Fig.17–7

18. Initial Tension
Shigley’s Mechanical Engineering Design

19. Flat Belt Tensions
Shigley’s Mechanical Engineering Design

20. Transmitted Horsepower
Shigley’s Mechanical Engineering Design

21. Correction Factors for Belts,
Based on Manufacturer Data
Shigley’s Mechanical Engineering Design

22. Velocity Correction Factor Cv for Leather Belts
Shigley’s Mechanical Engineering Design
Fig.17–9

23. Pulley Correction Factor CP for Flat Belts
Shigley’s Mechanical Engineering Design

24. Steps for Flat-Belt Analysis
Shigley’s Mechanical Engineering Design

25. Belt-Tensioning Schemes
Shigley’s Mechanical Engineering Design
Fig.17–11

26. Standard V-Belt Sections
Shigley’s Mechanical Engineering Design
Table 17–9

27. Inside Circumferences of Standard V-Belts
Shigley’s Mechanical Engineering Design
Table 17–10

28. Length Conversion Dimensions
Shigley’s Mechanical Engineering Design

29. V-Belt Pitch Length and Center-to-Center Distance
Shigley’s Mechanical Engineering Design

30. Horsepower Ratings of Standard V-Belts
Shigley’s Mechanical Engineering Design
Table 17–12

31. Adjusted Power
Shigley’s Mechanical Engineering Design

32. Angle of Wrap Correction Factor
Shigley’s Mechanical Engineering Design
Table 17–13

33. Belt-Length Correction Factor
Shigley’s Mechanical Engineering Design
Table 17–14

34. Belting Equation for V-Belt (Gates Belting)
Shigley’s Mechanical Engineering Design

35. Design Power for V-Belt
Shigley’s Mechanical Engineering Design
Number of belts:

36. V-Belt Tensions
Shigley’s Mechanical Engineering Design

37. Belting Selection
Shigley’s Mechanical Engineering Design
Use Belting Manufacture Specific Data
For examples Gates Belts (know mostly for V-belts)
https://www.gates.com/us/en.html
Available Resources from the Manufacturer
• Products and Applications (by Industry)
• Engineering Applications & Design Software
• Calculators
• Resources Library

38. Roller Chain
Shigley’s Mechanical Engineering Design

39. Roller Chain Characteristics
Shigley’s Mechanical Engineering Design
• Similar to Timing Belts, no slip
• Long life
• Fairly large power can be transmitted
• Costs less than gears
• Easy to adjust centers, tolerant of large variation
• Input and Output sprocket usually rotate in same direction
• Only need light to no chain preload tension
when installing, but may require a tensioner/idler
• Usually requires lubrication
• Can use multiple strands for increased power
• Usually made of steel
• Stainless steel versions available for food industry

40. Roller Chain
Shigley’s Mechanical Engineering Design
Fig.17–16

41. ANSI Chain Size Number
Shigley’s Mechanical Engineering Design
XXX
First number(s) pitch p in number of 1/8”
ANSI 40 chain is 4 x1/8” =0.50” pitch
0=Standard
1=Light Duty
ANSI 41 chain is 4 x1/8” =0.50” pitch
But Light Duty

42. Dimensions of American Standard Roller Chains
Shigley’s Mechanical Engineering Design
Table 17–19

43. Engagement of Chain and Sprocket
Shigley’s Mechanical Engineering Design
Fig.17–17

44. Roller Chain Drive
Shigley’s Mechanical Engineering Design
D2, N2
D1, N1

45. Roller Chain Design Guide Rules of Thumb
Shigley’s Mechanical Engineering Design
• Min Teeth per Sprocket ~ 12 to 25
• Max Teeth per Sprocket ~120
• Max Speed Reduction ~7:1
• Min Wrap Angle ~ 120˚

46. Chain Velocity
Shigley’s Mechanical Engineering Design

47. Chordal Speed Variation (as chain not perfectly round)
Shigley’s Mechanical Engineering Design
Fig.17–18

48. Roller Chain Rated Horsepower Capacity
Shigley’s Mechanical Engineering Design

49. Roller Chain Rated Horsepower Capacity
Shigley’s Mechanical Engineering Design

50. Available Sprocket Tooth Counts
Shigley’s Mechanical Engineering Design

51. Example 17–5
Shigley’s Mechanical Engineering Design

52. Example 17–5
Shigley’s Mechanical Engineering Design

53. Example 17–5
Shigley’s Mechanical Engineering Design

54. Wire Rope
Shigley’s Mechanical Engineering Design
Fig.17–19

55. Berg cable timing belts
Shigley’s Mechanical Engineering Design

56. Stress in Wire Rope
Shigley’s Mechanical Engineering Design

57. Wire-Rope Data
Shigley’s Mechanical Engineering Design
Table 17–24

58. Equivalent Bending Load in a Pulley, diameter D
 Wire rope tension giving same tensile stress as sheave bending is
called equivalent bending load Fb
 Clearly the smaller the sheave diameter the higher the added
bending tension of the sheave on the cable
Shigley’s Mechanical Engineering Design

59. Percent Strength Loss for D/d
Shigley’s Mechanical Engineering Design
Fig.17–20
D is sheave (pulley) diameter
d is the cable diameter

60. Minimum Factors of Safety for Wire Rope
Shigley’s Mechanical Engineering Design
Table 17–25

61. Bearing Pressure of Wire Rope in Sheave Groove
Shigley’s Mechanical Engineering Design

62. Maximum Allowable Bearing Pressures (in psi)
Shigley’s Mechanical Engineering Design
Table 17–26

63. Relation Between Fatigue Life of Wire Rope and Sheave Pressure
Shigley’s Mechanical Engineering Design
Fig.17–21

64. Fatigue of Wire Rope
 Fig. 17–21does not preclude failure by fatigue or wear
 It does show long life if p/Su is less than 0.001.
 Substituting this ratio in Eq. (17–42),
 Dividing both sides of Eq. (17–42) by Su and solving for F, gives
allowable fatigue tension,
 Factor of safety for fatigue is
Shigley’s Mechanical Engineering Design

65. Factor of Safety for Static Loading
 The factor of safety for static loading is
Shigley’s Mechanical Engineering Design

66. Typical Strength of Individual Wires
Shigley’s Mechanical Engineering Design

67. Service-Life Curve Based on Bending and Tensile Stresses
Shigley’s Mechanical Engineering Design
Fig.17–22

68. Some Wire-Rope Properties
Shigley’s Mechanical Engineering Design

69. Working Equations for Mine-Hoist Problem
Shigley’s Mechanical Engineering Design

70. Working Equations for Mine-Hoist Problem
Shigley’s Mechanical Engineering Design

71. Working Equations for Mine-Hoist Problem
Shigley’s Mechanical Engineering Design

72. Example 17–6
Shigley’s Mechanical Engineering Design
Fig.17–23

73. Example 17–6
Shigley’s Mechanical Engineering Design

74. Example 17–6
Shigley’s Mechanical Engineering Design

75. Example 17–6
Shigley’s Mechanical Engineering Design

76. Flexible Shaft Configurations
Shigley’s Mechanical Engineering Design
Fig.17–24b

77. Flexible Shaft Construction Details
Shigley’s Mechanical Engineering Design
Fig.17–24a