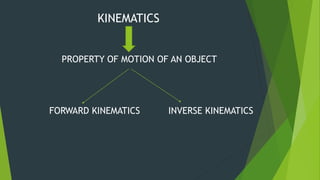
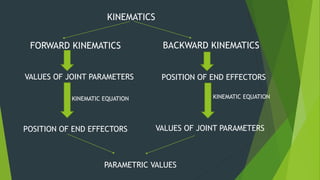
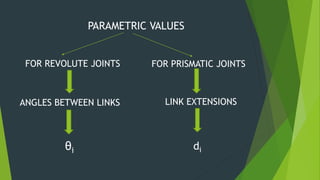
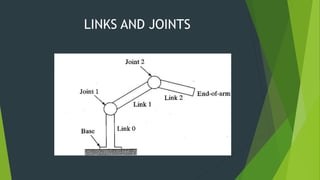
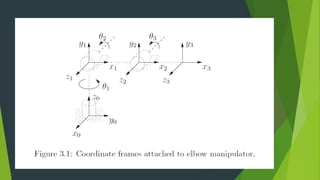
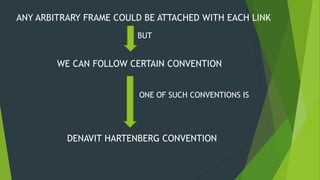
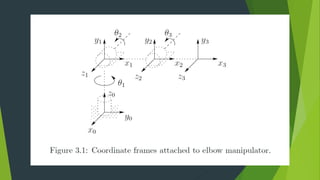
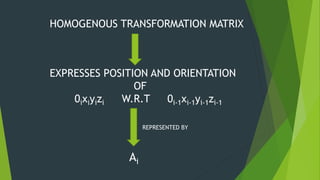
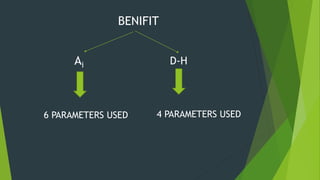
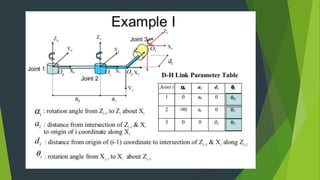
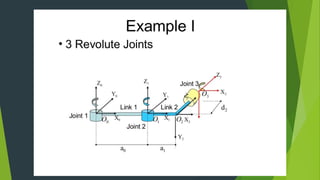
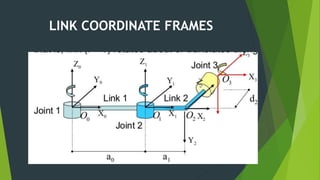
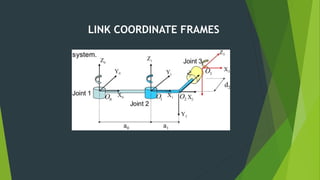
The Denavit-Hartenberg (D-H) convention provides a standardized method to define coordinate frames for each link of a robot manipulator. It uses four parameters - link length (ai), joint angle (αi), link offset (di), and joint twist (θi) - to define the transformation from one link's frame to the next. By applying the homogeneous transformation matrices for each link according to their D-H parameters, the forward kinematics can be calculated to determine the end effector position from the joint parameters. The D-H convention reduces the number of parameters needed compared to other methods.

1. DENAVIT HARTENBERG
ALGORITHM
Hitesh Mohapatra
https://www.linkedin.com/in/hiteshmohapatra/

2. WHAT IS KINEMATICS ?

3. KINEMATICS
PROPERTY OF MOTION OF AN OBJECT
FORWARD KINEMATICS INVERSE KINEMATICS

4. KINEMATICS
FORWARD KINEMATICS BACKWARD KINEMATICS
VALUES OF JOINT PARAMETERS POSITION OF END EFFECTORS
KINEMATIC EQUATION
POSITION OF END EFFECTORS VALUES OF JOINT PARAMETERS
KINEMATIC EQUATION
PARAMETRIC VALUES

5. PARAMETRIC VALUES
FOR REVOLUTE JOINTS FOR PRISMATIC JOINTS
ANGLES BETWEEN LINKS LINK EXTENSIONS
θi di

6. LINKS AND JOINTS

7. IF ‘N+1’ LINKS
THEN
‘N’ JOINTS

9. ANY ARBITRARY FRAME COULD BE ATTACHED WITH EACH LINK
BUT
WE CAN FOLLOW CERTAIN CONVENTION
DENAVIT HARTENBERG CONVENTION
ONE OF SUCH CONVENTIONS IS

10. WHAT IS THE BENEFIT?

11. IF FRAME
00x0y0z0
ATTACHED WITH ROBOT’S BASE
INERTIAL FRAME

13. HOMOGENOUS TRANSFORMATION MATRIX
EXPRESSES POSITION AND ORIENTATION
OF
0ixiyizi W.R.T 0i-1xi-1yi-1zi-1
REPRESENTED BY
Ai

14. HOMOGENOUS TRANSFORMATION MATRIX
HENCE, IN D-H CONVENTION Ai IS REPRESENTED AS A PRODUCT
OF FOUR BASIC TRANSFORMATIONS

15. BENIFIT
Ai D-H
6 PARAMETERS USED 4 PARAMETERS USED

16. LINK AND JOINT PARAMETERS
• JOINT ANGLE (θi) : THE ANGLE OF ROTATION FROM Xi-1 AXIS TO THE Zi-1 AXIS.
IT IS THE JOINT VARIABLE IF JOINT I IS ROTATORY.
• JOINT DISTANCE (di) : THE DISTANCE FROM THE ORIGIN OF (i-1) CO-ORDINATE
SYSTEM TO THE INTERSECTION OF THE ZI-1 AXIS AND Xi AXIS ALONG THE Zi-1 AXIS.
IT IS THE JOINT VARIABLE IF JOINT I IS PRISMATIC.
• LINK LENGTH (aI) : THE DISTANCE FROM THE INTERSECTION OF Zi-1 AXIS AND
THE Xi AXIS TO THE ORIGIN OF THE Ith CO-ORDINATE SYSTEM ALONG THE Xi.
• LINK TWIST ANGLE (αi) : THE ANGLE OF ROTATION FROM THE Zi-1 AXIS TO THE
Zi-1 AXIS ABOUT Xi AXIS.

18. EXAMPLE : TWO LINK ELBOW MANIPULATOR

20. D-H CONVENTION ALGORITHM
STEP-1:
LOCATE AND LABEL THE JOINT AXES
Z0,………..,Zn-1.
STEP-2:
ESTABLISH THE BASE FRAME . SET THE
ORIGIN ANYWHERE ON THE Z0 AXIS. THE
X0 AND Y0 AXES ARE CHOSEN CONVENIENTLY
TO FORM A RIGHT HAND FRAME.

21. STEP-3:
LOCATE THE ORIGIN OI WHERE THE
COMMON NORMAL TO Zi AND Zi-1 INTERSECTS
Zi. IF Zi INTERSECTS Zi-1 LOCATE Oi AT THIS
INTERSECTION. IF Zi AND Zi-1 ARE PARALLEL,
LOCATE Oi IN ANY CONVENIENT POSITION
ALONG Zi.
STEP-4:
ESTABLISH Ti ALONG THE COMMON
NORMAL BETWEEN Zi-1 AND Zi THROUGH Oi, IN
THE DIRECTION NORMAL TO THE Zi-1 – Zi
PLANE IF Zi-1 AND Zi INTERSECT.

22. STEP-5:
ESTABLISH Yi TO COMPLETE A RIGHT
HAND FRAME.

23. STEP-6:
ESTABLISH THE END EFFECTOR FRAME 0nXnYnZn.
ASSUMING THE N-TH JOINT IS REVOLUTE, SET Zn = A ALONG
THE DIRECTION Zn-1. ESTABLISH THE ORIGIN 0N
CONVENIENTLY ALONG Zn, PREFERABLY AT THE CENTER OF
GRIPPER OR AT THE TIP OF ANY TOOL THAT THEMANIPULATOR
MAY BE CARRYING. SET Yn = S IN THE DIRECTION OF GRIPPER
CLOSURE AND SET Xn = N AS S×A. IF THE TOOL IS NOT A
SIMPLE GRIPPER SET Xn AND Yn CONVENIENTLY TO FORM A
RIGHT HAND FRAME.

24. STEP-7:
CREATE A TABLE OF LINK PARAMETERS Ai, Di, Αi, Θi.
Ai = DISTANCE ALONG Xi FROM 0i TO THE INTERSECTION OF THE
Xi AND Zi-1 AXES.
Di = DISTANCE ALONG Zi-1 FROM 0i-1 TO THE INTERSECTION OF
THE Xi AND Zi-1 AXES. Di IS VARIABLE IF JOINT I IS PRISMATIC.
αi = THE ANGLE BETWEEN Zi-1 AND Zi MEASURED ABOUT Xi.

26. LINK COORDINATE FRAMES

27. ASSIGN LINK COORDINATE FRAMES:
TO DESCRIBE THE GEOMETRY OF ROBOT MOTION , WE ASSIGN A
CARTESIAN COORDINATE
FRAME (0i, Xi, Yi, Zi) TO EACH LINK, AS FOLLOWS:
 ESTABLISH A RIGHT-HANDED ORTHO-NORMAL COORDINATE FRAME
00 AT THE SUPPORTING BASE WITH Z0 LYING ALONG JOINT 1 MOTION
AXIS.
 THE Zi AXIS IS DIRECTED ALONG THE AXIS OF MOTION OF JOINT
(I+1) , THAT IS , LINK (I+1) ROTATES ABOUT OR TRANSLATES ALONG Zi.

28. LOCATE THE ORIGIN OF THE ITH COORDINATE AT THE
INTERSECTION OF Zi & Zi-1 OR AT THE INTERSECTION OF
COMMON NORMAL BETWEEN Zi & Zi-1 AXES AND THE Zi AXIS.
THE Xi AXIS LIES ALONG THE COMMON NORMAL FROM THE
Zi-1 AXIS TO THE Zi AXIS
Xi = ±(Zi-1 × Zi) / ||Zi-1× Zi|| , (IF Zi-1 IS PARALLEL TO Zi,
THEN Xi IS SPECIFIED ARBITRARILY, SUBJECT ONLY TO Xi
BEING PERPENDICULAR TO Zi)

29. LINK COORDINATE FRAMES

30. ASSIGN YI = +(Zi × Xi)/ ||Zi × Xi|| TO COMPLETE THE RIGHT HANDED
COORDINATE SYSTEM.
THE HAND COORDINATE FRAME IS SPECIFIED BY THE GEOMETRY OF THE
END EFFECTOR.
NORMALLY ,ESTABLISH Zn ALONG Zn-1 AXIS AND POINTING AWAY FROM THE
ROBOT; ESTABLISH Xn
SUCH THAT IT IS NORMAL TO BOTH Zn-1 AND Zn AXES. ASSIGN Yn TO
COMPLETE THE RIGHT HANDED COORDINATE SYSTEM.