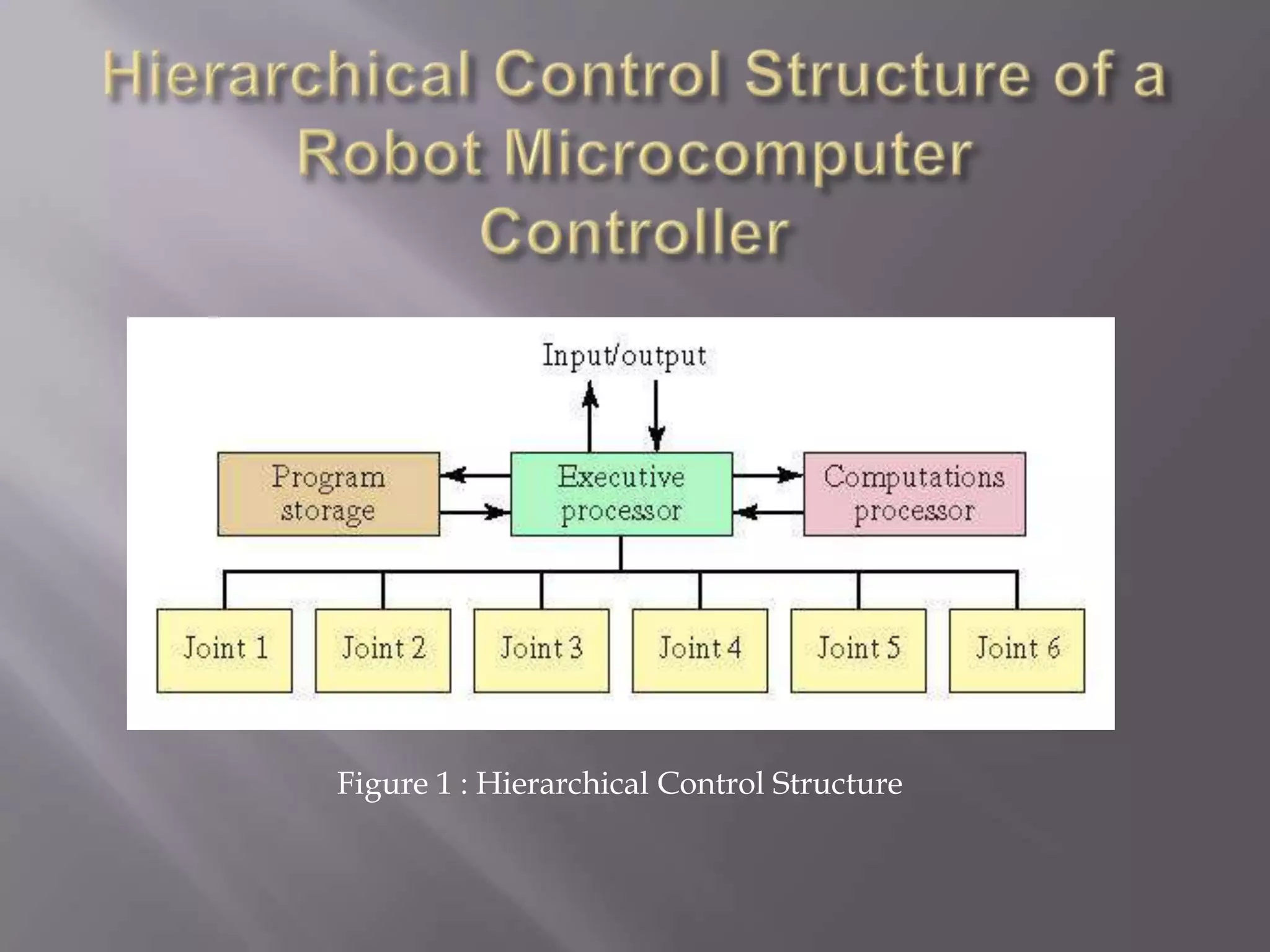
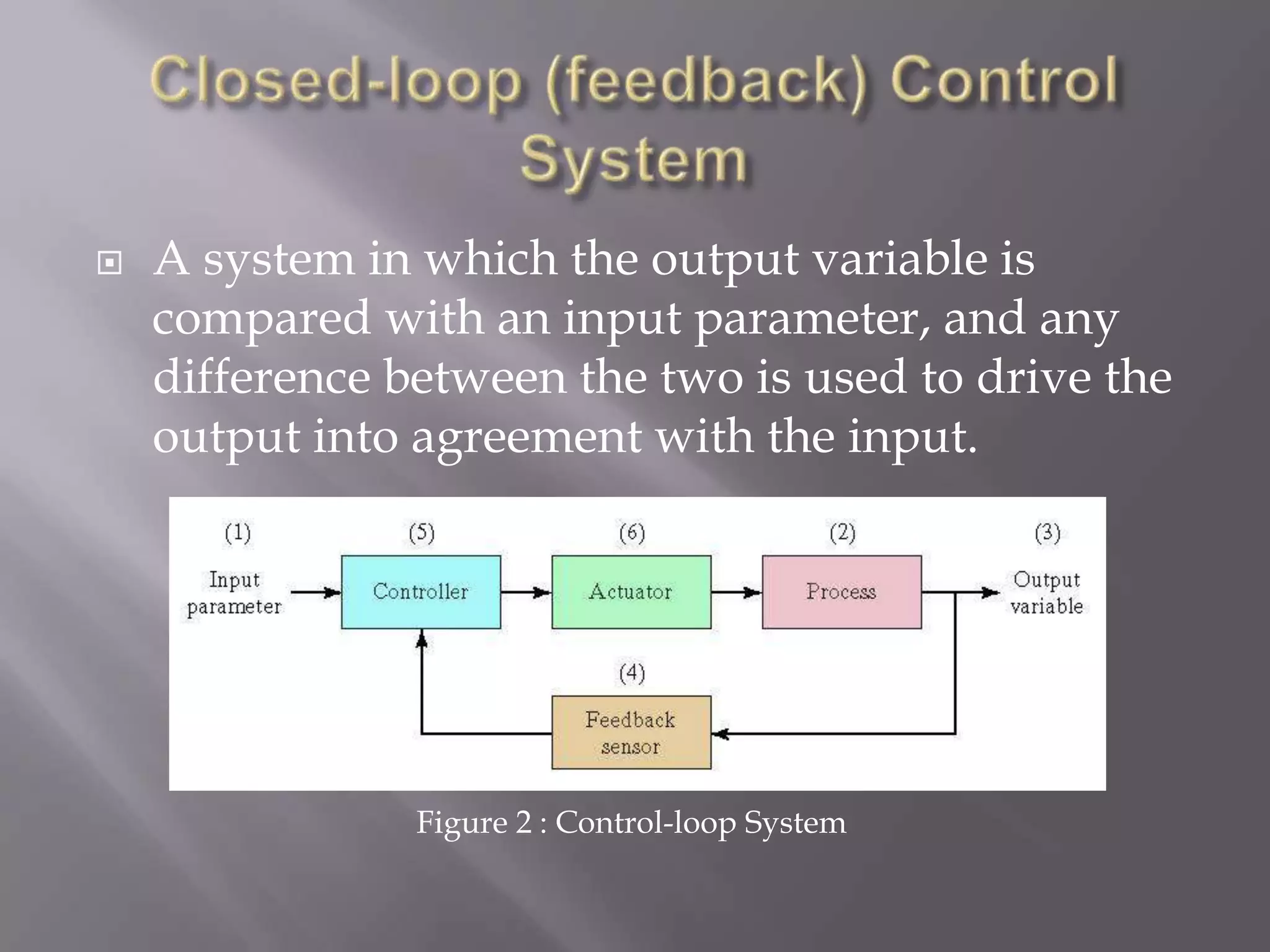
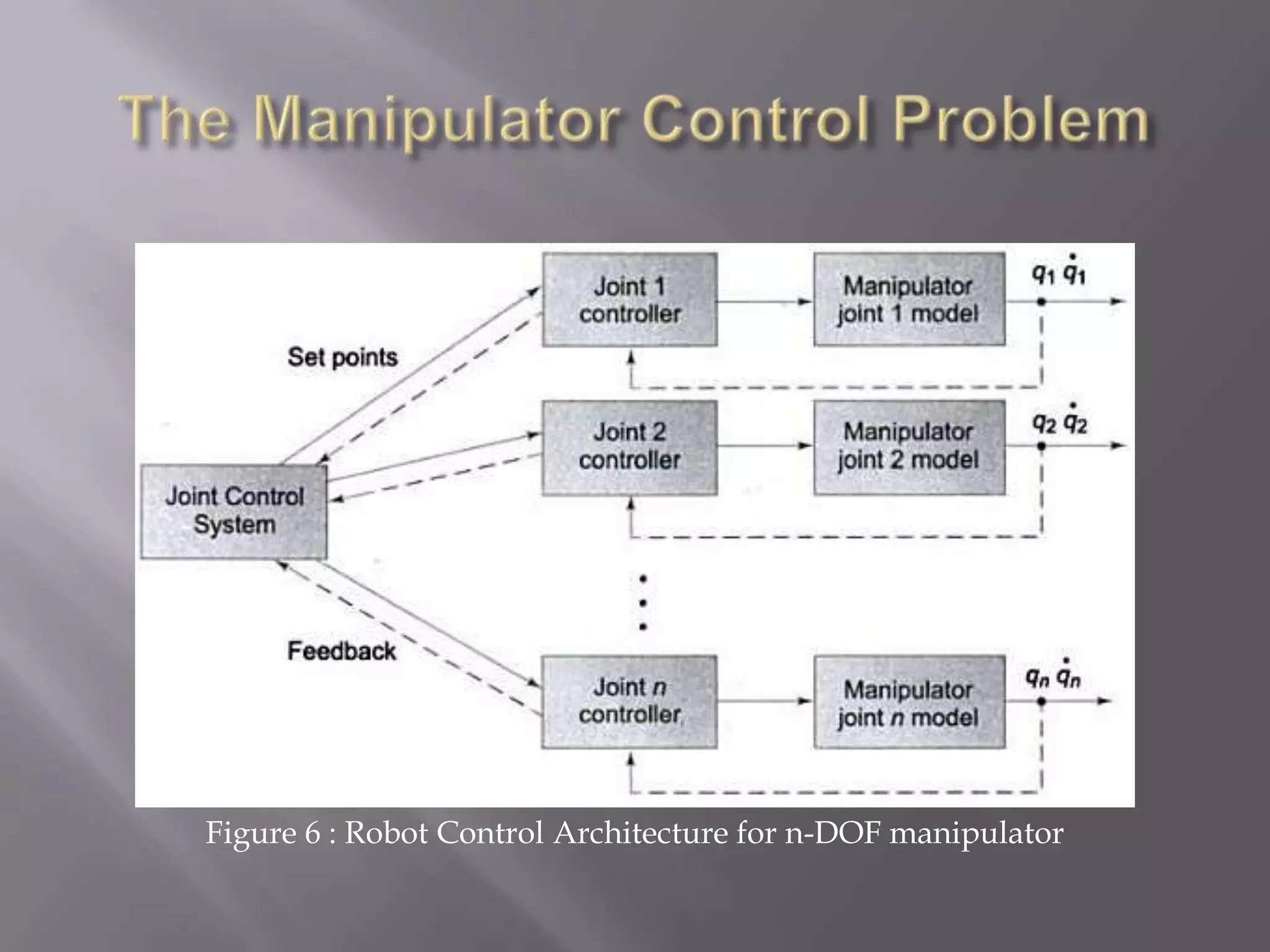
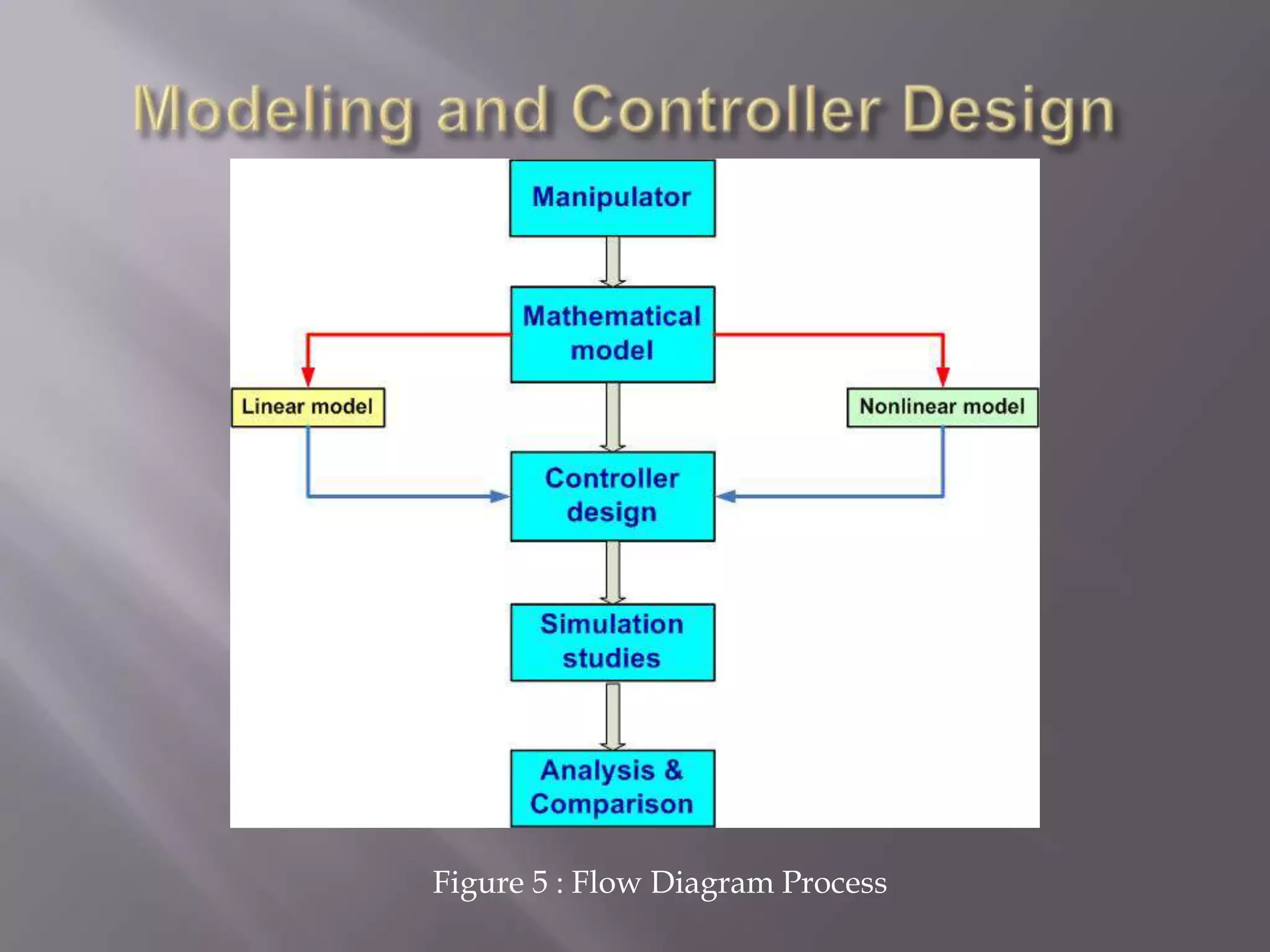
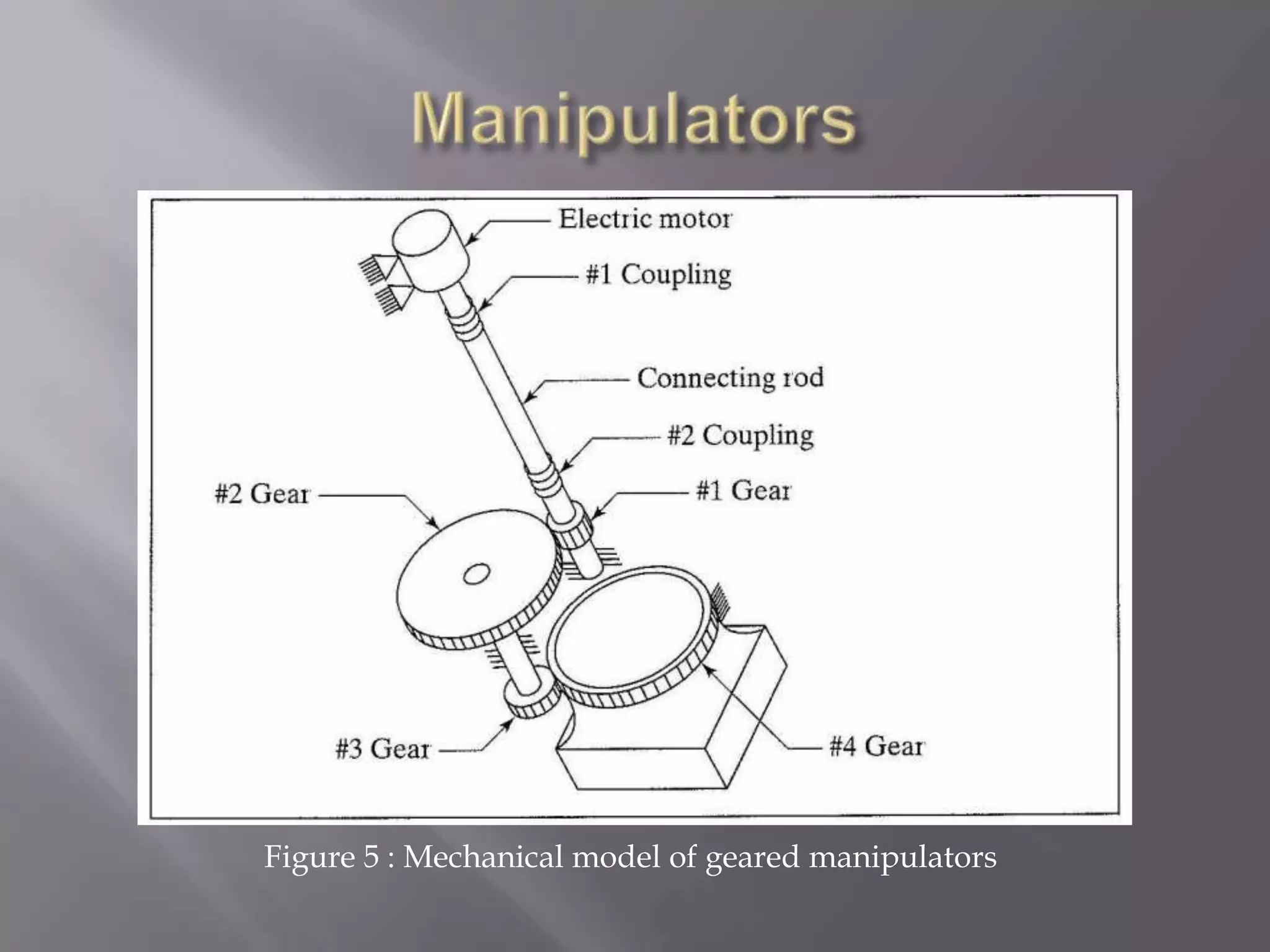
The document discusses control systems for robot manipulators. It covers open-loop and closed-loop control systems, with closed-loop being preferred using feedback. It describes using linear control techniques to approximate manipulator dynamics and designing controllers to meet stability and performance specifications. Common control techniques for manipulators are also summarized like PD, PID, state space control and adaptive/intelligent methods.

1. MOHAMMAD SYAZWAN BIN TALIB B020910019
MUHAMAD HAFFIZ BIN MOHD RADZI B020910190
MUHAMMAD SHAKIR BIN SULAIMAN B020810095
MUHAMMAD FARHAN BIN MOHD ROSLAN B020910115
EN. RIDZA AZRI BIN RAMLEE
FAKULTI KEJURUTERAAN ELEKTRONIK & KEJURUTERAAN
KOMPUTER

2.  To learn open-loop and close loop system
 To learn linear and nonlinear control
 To design a simple manipulator controller
based on several techniques

3.  Limited Sequence Control – pick-and-place
operations using mechanical stops to set positions.
 Playback with point to point control – records
work cycle as a sequence of points, then plays back
the sequence during program execution.
 Playback with continuous path control – greater
memory capacity and/or interpolation capability
to execute paths (in addition to points).
 Intelligent control – exhibits behavior that makes it
seem intelligent, e.g., responds to sensor
inputs, makes decisions, communicates with
humans.

4.  Electric
– Uses electric motors to actuate individual joints
– Preferred drive system in today's robots
 Hydraulic
– Uses hydraulic pistons and rotary vane actuators
– Noted for their high power and lift capacity
 Pneumatic
– Typically limited to smaller robots and simple
material transfer applications

5. Figure 1 : Hierarchical Control Structure

6.  Closed-loop (feedback) control system
 Open-loop control system

7.  A system in which the output variable is
compared with an input parameter, and any
difference between the two is used to drive the
output into agreement with the input.
Figure 2 : Control-loop System

8.  operates without the feedback loop
 Simpler and less expensive
 Risk that the actuator will not have the
intended effect
Figure 3 : Open-loop System

9.  Linear Control of Manipulators
 Feedback and Closed-loop Control
Figure 4 : Block Diagram Manipulator Control System

10.  The initial and the final location of end-effector in Cartesian space, specified
by the transformation matrices Tinitial and Tfinal, serve as the input.
 The inverse kinematics model computes the desired end-effector location in
joint space.
 Then, a trajectory generator computes the joint-position time
histories, based on the joint-space algorithms.
 Depending on the servo error computed from the base reference values and
the sensor measurements, the control system commands the individual
actuators to achieve the desired motion.
Figure 5 : Operation for point-to point motion control of a manipulator

11.  The use of linear-control techniques is valid only when the
system being studied can be modeled mathematically by
linear differential equations.
 We have to calculate joint position time histories that
correspond to desired end-effector motions through space.
 For the case of manipulator control, such linear methods
must be viewed as approximate methods, for the dynamics
of a manipulator are more properly represented by a
nonlinear differential equation.
 It is often reasonable to make such approximations
methods are most often used in current industrial practice.
 The justification for using linear controllers is not only
empirical.
 There is a certain linear controller leads to a reasonable
control system even without resorting to a linear
approximation of manipulator dynamics.

12.  A control system that makes use of feedback is called a
closed-loop control system. The "loop" closed by such
a control system around the manipulator is apparent in
the figure.
 The only way to build a high-performance control
system is to make use of feedback from joint
sensors, as indicated in the figure.
 Typically, this feedback is used to compute the servo
error by finding the difference between the desired
and the actual position and that between the desired
and the actual velocity.
 The control system can then compute how much
torque is required as a function to reduce servo errors.

13.  The central problem is designing a closed-loop system
that meets certain performance specifications.
 First of all, the system has to remain stable. We will
define a system to be stable, if the errors remain "small"
when executing various desired trajectories even in the
presence of some disturbances. An improperly designed
control system can sometimes result in unstable
performance, in which servo errors are enlarged instead
of reduced.
 The second requirement is that the closed-loop
performance of the system is satisfactory. In
practice, such "proofs" range from mathematical proofs
based on certain assumptions and models to more
empirical results, such as those obtained through
simulation or experimentation.

14. Figure 6 : Robot Control Architecture for n-DOF manipulator

15.  The manipulator control problem is a multi-
input, multi-output (MIMO)problem, involving joint
and the end-effector
locations, velocities, accelerations, and force vectors.
 To simplify the problem, each joint is considered to be
independent and separately controlled.
 This single-joint model is assumed to have a single
input(set point) and single
output(location, velocity, etc..).
 Hence, the n-DOF manipulator is modelled as n-
independent linear second-order system and is
controlled by n-independent single-input, single-
output (SISO)control systems.
 Before developing and analyzing the linear second-
order SISO model of the joint, the general second-order
linear system characteristics are briefly brushed up
first.

16. To overcome unmodeled dynamics, variable
payloads, fiction and disturbance torque, variation
and noise, we use nonlinear control to :
 Tracking, regulate state, state set point
 Ensure the desired stability properties
 Ensure the appropriate transients
 Reduce the sensitivity to plant parameters

17. A lot of techniques that are used for nonlinear
systems come from linear systems, because:
 Nonlinear systems can (sometime) be
approximated by linear systems.
 Nonlinear systems can (sometime) be
“transformed "into linear systems.
 The tools are generalized and extended.

18. Figure 5 : Flow Diagram Process

19. Figure 5 : Mechanical model of geared manipulators

20.  Transfer Function
 State Space

21.  Proportional and Derivative Control (PD)
 Proportional Integral and Derivatives (PID)
 State Space Controller (Poles Placement
Technique)
 Artificial Intelligence Controller (Fuzzy Logic &
Neural Network)
 Adaptive Cruise Controller (ACC)
 Cooperative Adaptive Cruise Controller (CACC)
 Model Predictive Controller (MPC).
 Robust Control and etc..

22.  John J. Craig - Introduction To Robotics -
Mechanics And Control.
 R K Mittal & I J Nagrath, “Robotics and
Control”, Tata McGraw-Hill Publishing
Company. Ltd., New Delhi,2003