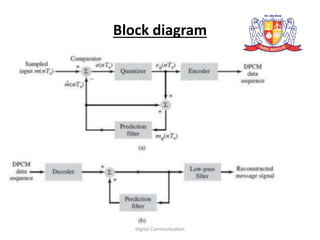
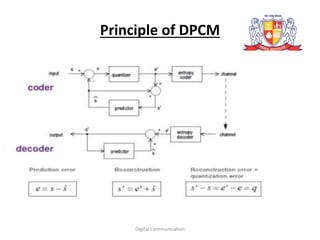
Differential pulse-code modulation (DPCM) encodes signals by taking the difference between the current sample and a prediction of the next sample based on previous samples. This difference signal has a smaller range than the original signal and can be more efficiently quantized and encoded. DPCM uses a feedback loop where the difference is quantized, sent to the receiver, and added to the previous reconstructed sample to estimate the current sample. Adaptive delta modulation is a variant of DPCM where the quantization step size varies depending on the number of consecutive bits in the same direction to reduce errors. DPCM can reconstruct signals sampled above the Nyquist rate but may suffer from error drift or error propagation issues over multiple samples.

1. Differential pulse-code
modulation
By:-
•Dharit Unadkat -130870111039
Guided By:-
•Prof.Bharat Tank
•Prof.Ketan Goswami
Class:-
EC-6th sem,
Parul Institute of Technology,
Limda.
Digital Communication

2. Introduction
• Differential pulse-code modulation (DPCM) is a signal
encoder that uses the baseline of pulse-code modulation
(PCM) but adds some functionalities based on the prediction
of the samples of the signal. The input can be an analog signal
or a digital signal.
• If the input is a continuous-time analog signal, it needs to
be sampled first so that a discrete-time signal is the input to the
DPCM encoder.
Digital Communication

3. • Option 1: take the values of two consecutive samples; if
they are analog samples, quantize them; calculate the
difference between the first one and the next; the output is
the difference, and it can be further entropy coded.
• Option 2: instead of taking a difference relative to a
previous input sample, take the difference relative to the
output of a local model of the decoder process; in this
option, the difference can be quantized, which allows a
good way to incorporate a controlled loss in the encoding.
Digital Communication

4. Block diagram
Digital Communication

5. Principle of DPCM
Digital Communication

6. Adaptive delta modulation
• Adaptive delta modulation or [continuously variable slope
delta modulation] (CVSD) is a modification of DM in
which the step size is not fixed. Rather, when several
consecutive bits have the same direction value, the encoder
and decoder assume that slope overload is occurring, and
the step size becomes progressively larger.
• Otherwise, the step size becomes gradually smaller over
time. ADM reduces slope error, at the expense of increasing
quantizing error.This error can be reduced by using a low-
pass filter. ADM provides robust performance in the
presence of bit errors meaning error detection and
correction are not typically used in an ADM radio design,
this allows for a reduction in host processor workload
(allowing a low-cost processor to be used).
Digital Communication

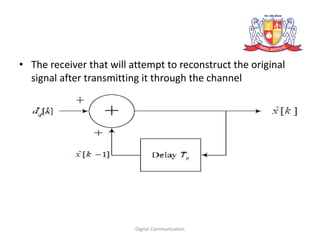
7. ANALYSIS OF DPCM
• Consider a signal x(t) that is sampled to obtain the
samples x(kTs), where Ts is the sampling period
and k is an integer representing the sample number.
For simplicity, the samples can be written in the
form x[k], where the sample period Ts is implied.
Assume that the signal x(t) is sampled at a very
high sampling rate. We can define d[k] to be the
difference between the present sample of a signal
and the previous sample, or
d [k ] = x [k ]− x [k −1].
Digital Communication

8. • Now this signal d[k] can be quantized instead of x[k] to
give the quantized signal dq[k].
As mentioned above, for signals x(t) that are sampled at a
rate much higher than the Nyquist rate, the range of values
of d[k] will be less than the range of values of x[k].
After the transmission of the quatized signal dq[k],
theoretically we can reconstruct the original signal by doing
an operation that is the inverse of the above operation. So,
we can Obtain an approximation of x[k] using
x^[k]=dq[k]+x^[k-1]
Digital Communication

9. So, if dq[k] is close to d[k], it appears from the above
equation that obtained xˆ[k ] will be close to d[k].
Digital Communication

10. • The receiver that will attempt to reconstruct the original
signal after transmitting it through the channel
Digital Communication

11. • Because we are quantizing a difference signal and
transmitting that difference over the channel, the
reconstructed signal may suffer from one or two possible
problems
Digital Communication

12. NYQUIST’S SAMPLING THEOREM
• According to the Nyquist sampling criterion, a signal must
be sampled at a sampling rate that is at least twice the
highest frequency in the signal to be able to reconstruct it
without aliasing.
• If g(t) is a continuous time signal with bandwidth B Hz
then it can be reconstructed exactly by its samples as long
as the sampling frequency is greater than 2B Hz.
Digital Communication

13. • The minimum sampling rate fs = 2B Hz required to
recover g(t) from its samples is called NYQUIST RATE
of sampling.
• The corresponding sampling interval
Ts = 1/22B
is called NYQUIST INTERVAL for g(t).
Digital Communication

14. Thank You
Digital Communication