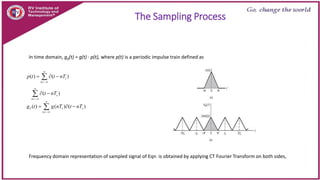
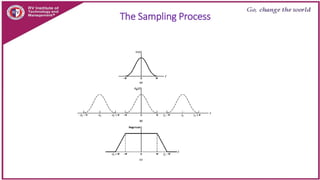
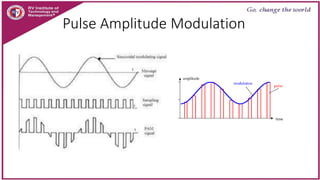
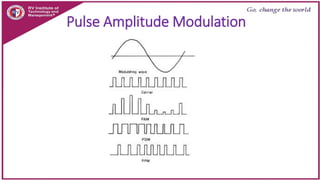
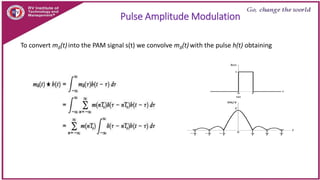
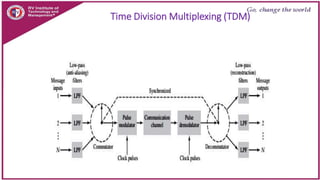
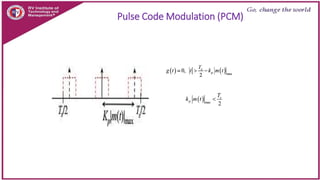
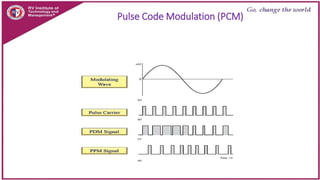
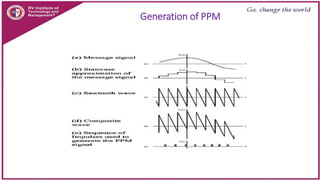
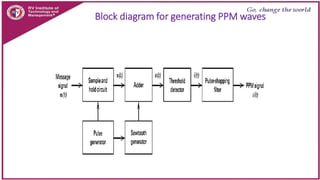
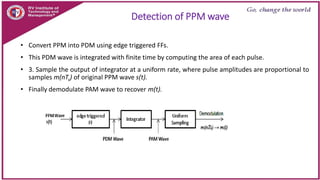
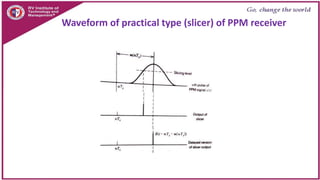
This document discusses principles of communication systems including sampling, quantization, pulse amplitude modulation (PAM), time division multiplexing (TDM), and pulse position modulation (PPM). It provides details on how analog signals are converted to digital through sampling and quantization. It explains the generation and detection of PAM, TDM, and PPM signals. Key advantages of digital transmission and various modulation techniques are summarized.

1. Department of Electronics and Communication Engineering
Subject : Principles of Communication Systems
Course Code : 21EC44
Semester : 4TH Sem
Dr Nataraj V
Associate Professor,
Department of Electronics and Communication Engineering
RVITM, Bengaluru - 560076

2. MODULE - IV
SAMPLING AND QUANTIZATION: Introduction, Why Digitize
Analog Sources? The Low pass Sampling process Pulse Amplitude
Modulation. Time Division Multiplexing, Pulse-Position
Modulation, Generation of PPM Waves, Detection of PPM
Waves.

3. Introduction
• A continuous analog signal into a digital signal has two sub-processes:
Sampling - conversion of a continuous-space/time(audio, video) signal into a
discrete-space/time (audio, video) signal.
Quantization - converting a continuous-valued (audio, video) signal that has a
continuous range (set of values that it can take) of intensities and/or colors into
a discrete-valued (audio, video) signal that has a discrete range of intensities
and/or colors; this is usually done by rounding, truncation or other irreversible
non-linear process of information destruction

4. Advantages of digital transmission
• Digital systems are less sensitive to noise than analog.
• For long transmission lengths, the signal may be regenerated effectively error-
free at different point along the path and the original signal transmitted over
the remaining length.
• With digital systems, it is easier to integrate different services.
• Example: video and the accompanying soundtrack, into the same transmission
scheme.
• The transmission scheme can be relatively independent of the source.
• Circuitry for handling digital signals is easier to repeat and digital circuits are
less sensitive to physical effect such as vibration and temperature.
• Digital signals are simpler to characterize and typically do not have the same
amplitude range and variability as analog signals.

5. Advantages of digital transmission
• Various media sharing strategies, known as multiplexing techniques, are more easily
implemented with digital transmission strategies.
• There are techniques for removing redundancy from a digital transmission, so as to minimize the
amount of information that has to be transmitted. These techniques fall under the broad
classification of source coding
• There are techniques for adding controlled redundancy to digital transmission, such that errors
occur during transmission may be corrected at the receiver without any additional information.
These techniques fall under the general. These techniques fall under the general category of
channel coding.
• Digital techniques make it easier to specify complex standards that may be shared on a
worldwide basis. This allows the development of communication components with many
different features (e.g., a cellular handset) and their interoperation with a different component
(e.g., a base station) produced by a different manufacturer.
• Other channel compensations techniques, such as equalization, especially adaptive versions, are
easier to implement with digital transmission techniques.

6. The Sampling Process
• Sampling process is used to convert a continuous-time signal into a discrete-time sequence. DT
signal, g(n) is obtained by extracting CT signal, g(t) every Ts seconds, where Ts is known as the
sampling period or interval.
• For lossless digitization, the sampling rate should be at least twice the maximum frequency
response. In mathematical terms:
fs > 2*fm
• Where fs is sampling frequency and fm is the maximum frequency in the signal

7. The Sampling Process
( ) ( )
s
n
p t t nT


  

( )
s
n
t nT


 

( ) ( ) ( )
s s
n
g t g nT t nT



  

In time domain, gδ(t) = g(t) ∙ p(t), where p(t) is a periodic impulse train defined as
Frequency domain representation of sampled signal of Eqn is obtained by applying CT Fourier Transform on both sides,

8. The Sampling Process
Reconstructing the signal of g(t):
• Provides an interpolation formula for reconstructing the original signal from the sequence of
sample values {g(n/2W)}
• sinc(2Wt) playing the role of an interpolation function
• Eqn (7) represents the convolution (or filtering) of the impulse train gδ(t) given by Eq. with the
impulse response sinc(2Wt).

9. The Sampling Process
• Any impulse response that plays the same roles as sinc(2Wt) is also referred
to as a reconstruction filter. The sampling theorem for strictly band-limited
signals of finite energy may be stated in two equivalent parts. A band-limited
signal of finite energy, which only has frequency components less than W Hz.
• It is completely described by specifying the values of the signal at instants of
time separated by 1/2W seconds.
• It may be, completely recovered from a knowledge of its samples taken at the
rate of 2W samples per second.
• The sampling rate of 2W samples per second, for a signal bandwidth of W Hz,
is called the Nyquist rate; its reciprocal 1/2W (measured in seconds) is called
Nyquist interval.

10. The Sampling Process

11. Pulse Amplitude Modulation
• In pulse-amplitude modulation (PAM), the amplitudes of regularly spaced pulses are
varied in proportion to the corresponding sample values of a continuous message
signal; the pulses can be of a rectangular form or some other shape. PAM is
somewhat similar to natural sampling, where the message signal is multiplied by a
periodic train of rectangular pulses. In natural sampling the top of each modulated
rectangular pulse varies with the message signal.
• Two steps are involved in the generation of the PAM signal.
• Instantaneous sampling of the message signal m(t) every Ts seconds, where the
sampling rate fs = 1/Ts is chosen in accordance with the sampling theorem.
Lengthening the duration of each sample so obtained to some constant value T.
• In digital circuit technology, these two operations are jointly referred to as “sample
and hold.”

12. Pulse Amplitude Modulation

13. Pulse Amplitude Modulation

14. Sample Hold Analysis: Let s(t) denote the sequence of flat-top pulses generated
when m(t) is convolved with train of h(t), which is a standard rectangular pulse of unit
amplitude and duration T, defined as
Pulse Amplitude Modulation

15. Pulse Amplitude Modulation
To convert mδ(t) into the PAM signal s(t) we convolve mδ(t) with the pulse h(t) obtaining

16. Pulse Amplitude Modulation
• Note that, using flat-top samples to generate a PAM signal, we have introduced
amplitude distortion as well as a delay of T/2 (known as aperture effect).
• This distortion may be corrected by connecting an equalizer in cascade with the low-
pass
reconstruction filter.
• The equalizer has the effect of decreasing the in-band loss of the
reconstruction filter. Ideally, the amplitude response of the equalizer is given
by,

17. Time Division Multiplexing (TDM)
• TDM is a method of transmitting and receiving multiple independent message signals over a
single transmission channel.
• Transmission of the message samples engages the communication channel for only a fraction of
the sampling interval on a periodic basis. Each message signal is first restricted in bandwidth by a
low pass pre-alias filter to remove the frequencies that are not essential which helps in reducing
the aliasing problem.
• The outputs of these filters are then applied to a commutator.
Electronic commutator :
• Sequentially samples each of the N input messages at a rate fs > 2W, where W is the cut-off
frequency of the pre-alias filter
• Combines them to form a composite base band signal, which travels through the channel.

18. Time Division Multiplexing (TDM)

19. Time Division Multiplexing (TDM)
• Pulse demodulator: Performs the reverse operation of the pulse
modulator.
• Decommutator: The narrow samples produced at the pulse
demodulator output are distributed to the appropriate low-pass
reconstruction filters.
• The decommutator operates in synchronism with the
commutator in the transmitter.

20. Pulse Position Modulation
• Pulse-Duration Modulation (PDM): This form of modulation is also referred to as Pulse-Width
Modulation. PWM is sometimes called pulse duration modulation (PDM) or pulse length
modulation (PLM), as the width (active portion of the duty cycle) of a constant amplitude pulse is
varied proportional to the amplitude of the message signal at the time the signal is sampled.
• The maximum analog signal amplitude produces the widest pulse, and the minimum analog
signal amplitude produces the narrowest pulse.
• Note, however, that all pulses have the same amplitude. Mathematical representation of PPM
signal using the sample m(nTs) of a message signal m(t) to modulate the position of nth pulse, is

21. Pulse Code Modulation (PCM)

22. Pulse Code Modulation (PCM)

23. Generation of PPM

24. Block diagram for generating PPM waves

25. Detection of PPM wave
• Convert PPM into PDM using edge triggered FFs.
• This PDM wave is integrated with finite time by computing the area of each pulse.
• 3. Sample the output of integrator at a uniform rate, where pulse amplitudes are proportional to
samples m(nTs) of original PPM wave s(t).
• Finally demodulate PAM wave to recover m(t).

26. Waveform of practical type (slicer) of PPM receiver

27. • Due to constant amplitude of PPM pulses, the information is
not obtained in the amplitude. Hence the noise added to the
PPM signal does not distort the information. Thus it has good
noise immunity.
• It is possible to reconstruct PPM signal from the noise
contaminated PPM signal.
• Due to constant amplitude of pulses, the transmitted power
always remains constant. It does not change as it is used to in
PWM.
Advantages of PPM

28. Disadvantages of PPM
• As the position of PPM pulses is varied with reference to a reference
pulse, a transmitter has to send synchronizing pulses to operate the
timing circuits in the receiver.
• Without them the demodulation won’t be possible to achieve.
• Large bandwidth is required to ensure transmission of undistorted pulses.
Disadvantages of PPM