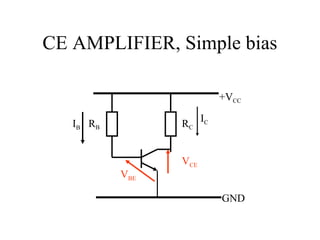
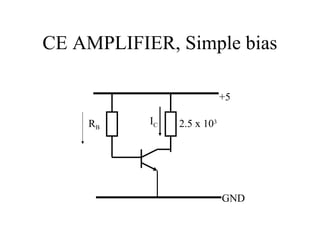
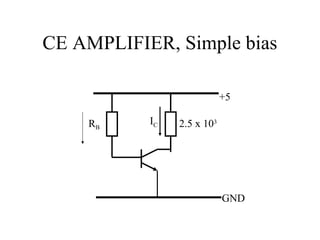
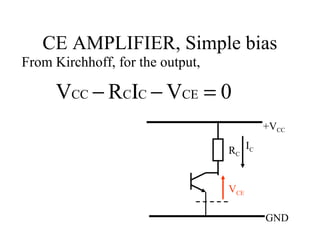
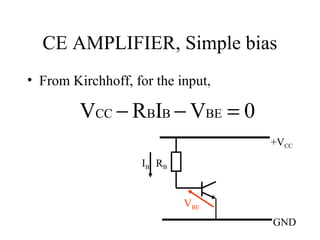
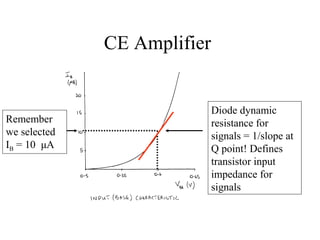
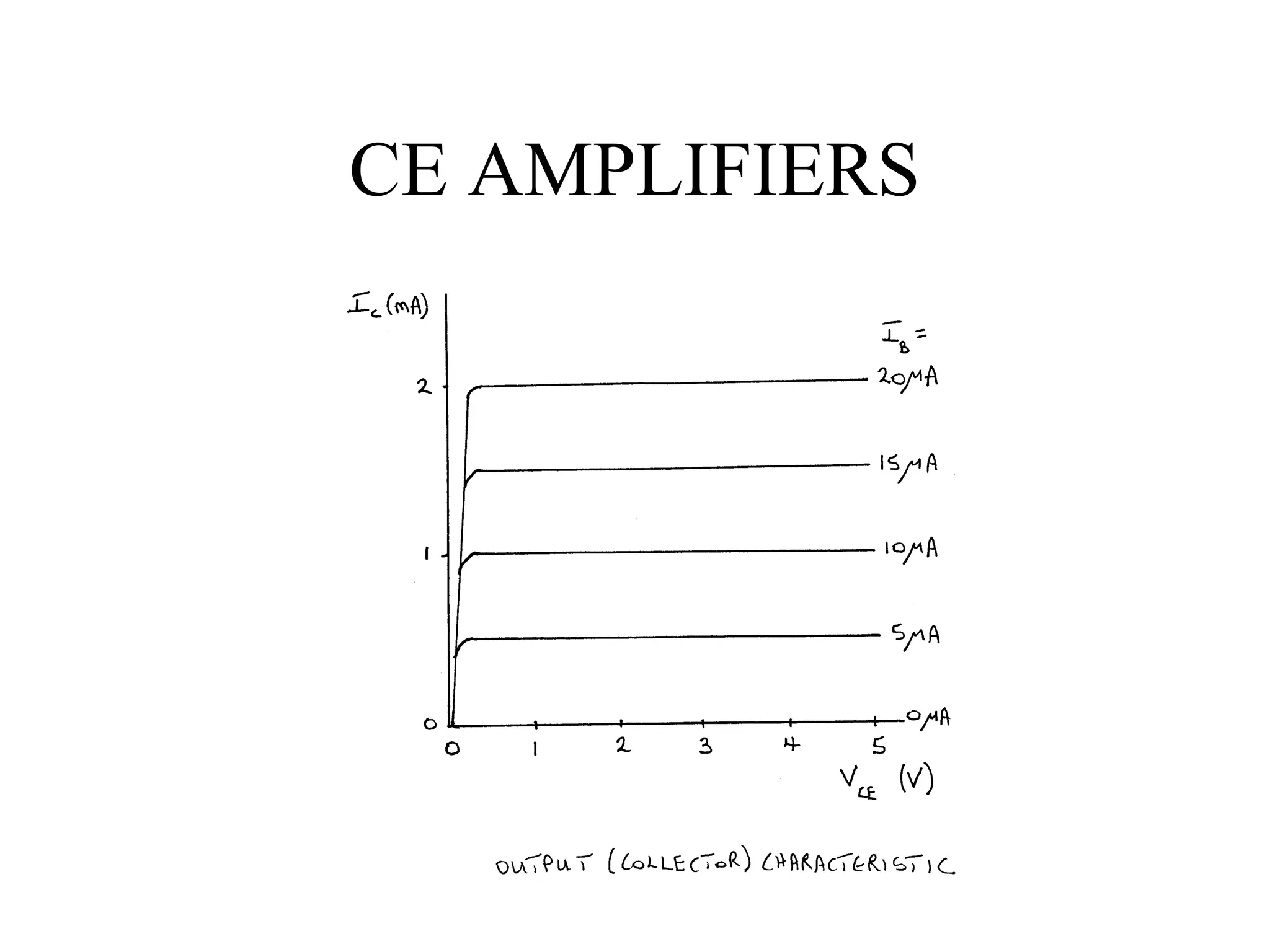
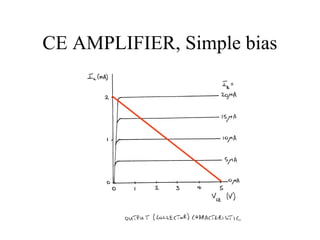
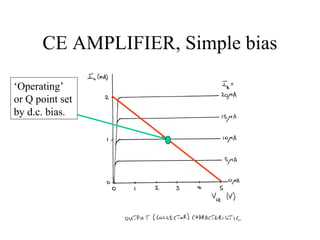
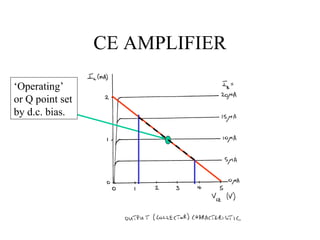
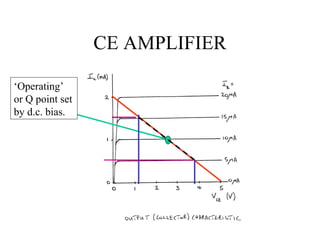
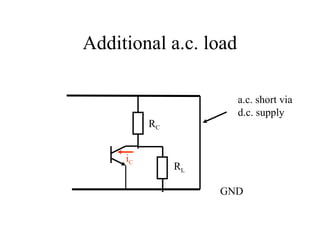
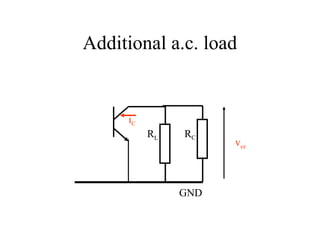
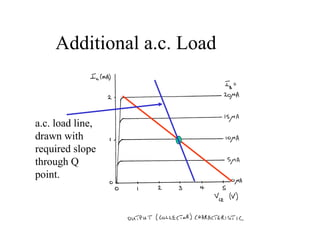
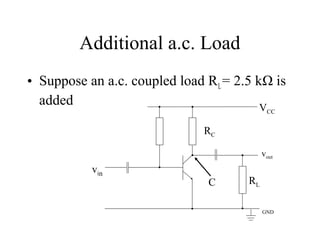
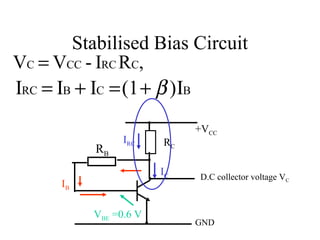
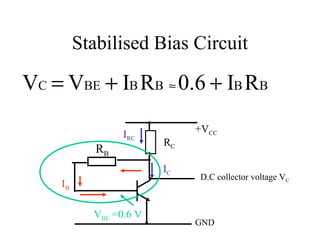
1) CE amplifiers use bias circuits to set an operating point for the transistor. Simple bias circuits vary with transistor parameters like beta. 2) Load line analysis graphs the interplay between circuit constraints and the transistor output characteristic to determine the operating point. 3) Stabilized bias circuits aim to fix the emitter current independently of beta using an emitter resistor and potential divider bias network. Negative feedback bias circuits also use feedback from the collector voltage.

1. CE AMPLIFIERS

2. CE AMPLIFIERS
• The first step is to set up an operating or ‘Q’
point using a suitable bias circuit.
• We will, by way of introduction, use a so
called load line technique to see the
interplay between the circuit and device
constraints on voltage and current.
• This will provide a graphical analysis of
amplifier behaviour.

3. CE AMPLIFIERS
• The following (simple) bias circuit uses a
single resistor RB to fix the base current.
• It is not very good since the
emitter/collector currents and hence the
operating point (IC, VCE) vary with β.
• This will be improved with stabilised bias
circuits in due course.

4. CE AMPLIFIER, Simple bias
+VCC
IB R B RC IC
GND

5. CE AMPLIFIER, Simple bias
+VCC
IB R B RC IC
VCE
VBE
GND

6. CE AMPLIFIER, Simple bias
• To enable us to look at a particular
numerical example we choose the supply
voltage VCC = 5V and RC = 2.5 kΩ

7. CE AMPLIFIER, Simple bias
+5
RB IC 2.5 x 103
GND

8. CE AMPLIFIER, Simple bias
• In later discussions an a.c. signal (and an
additional load resistor) will be coupled to the d.c.
circuit using coupling capacitors.
• The capacitor values are chosen so that their
impedance (1/ ωC) is negligibly small (zero) at the
a.c.(signal) frequency (or over the operating
frequency range).
• A capacitor acts as a short circuit for d.c. and the
d.c. bias circuit can be designed independently of
the a.c. source and any ‘a.c. load’.

9. CE AMPLIFIER, Simple bias
+5
RB IC 2.5 x 103
GND

10. CE AMPLIFIER, Simple bias
From Kirchhoff, for the output,
VCC − RCIC − VCE = 0
+VCC
RC I C
VCE
GND

11. CE AMPLIFIER, Simple bias
• Numerically, 5 - 2.5 x 103 IC-VCE =0
• Or, rearranging, IC = (5 – VCE )/ (2.5 x 103)
• A plot of IC against VCE is a straight line with
slope (– 1/ 2.5 x 103)
• It is called a load line and represents the
variation of IC with VCE imposed by the
circuit or load.

12. CE AMPLIFIER, Simple bias
• Another variation of IC with VCE is
determined by the output characteristic.

13. CE AMPLIFIER, Simple bias
• Another variation of IC with VCE is
determined by the output characteristic.
• The two relationships can be solved
graphically for IC and VCE.

14. CE AMPLIFIER, Simple bias
• Thus we calculate three points on the load
line IC = (5 – VCE )/ (2.5 x 103) as
IC =0, VCE =5V
IC = 1mA, VCE =2.5V
VCE =0V, IC =5/2500 A = 2mA.
• To enable us to plot it on the output
characteristic.

15. CE AMPLIFIER, Simple bias

16. CE AMPLIFIER, Simple bias
• The region along the load line includes all
points between saturation and cut-off.
• The base current IB should be chosen to
maximise the output voltage swing in the
linear region.
• Bearing in mind that VCE (Sat) ≈ 0.2 V and
VCE Max = 5V choose the operating (Q) point at
IB = 10 μA.

17. CE AMPLIFIER, Simple bias
‘Operating’
or Q point set
by d.c. bias.

18. CE AMPLIFIER, Simple bias
• From Kirchhoff, for the input,
VCC − RBIB − VBE = 0
+VCC
IB RB
VBE
GND

19. CE AMPLIFIER, Simple bias
• Remembering that VBE ~ 0.6 V (the base or
input characteristic is that of a forward
biased diode) we can find RB ~ 440 kΩ.

20. CE AMPLIFIER, Simple bias
• A a.c. signal is superimposed on top of the
d.c. bias level.
• We are interested in the voltage and current
gains for this a.c. component.

21. CE AMPLIFIER
VCC
IC
RB RC
RL
VCE
RS
Signal input Signal output
VS
GND

22. CE AMPLIFIER
• The Q (d.c. bias) value of VCE is about 2.5 V
• The maximum positive signal swing allowed is,
therefore (5-2.5) V = 2.5 V (The total
• The maximum negative voltage swing allowed is
(2.5 –0.2) V =2.3 V
• The maximum symmetric symmetric signal swing
about the Q point is determined by the smaller of
these, i.e. it is ±2.3 V.

23. CE Amplifier
• To find the voltage and current gains using
the load line method we must use the input
and output characteristics.

24. CE Amplifier
Diode dynamic
Remember resistance for
we selected signals = 1/slope at
IB = 10 μA Q point! Defines
transistor input
impedance for
signals

25. CE Amplifier
• From the input curve we estimate that as I B
changes by ±5μA about the bias level of
10μA then the corresponding change in VBE
is about 0.025 V.
• When iB =5μA, vBE = 0.5875V; when iB
=15μA, vBE = 0.6125.
∆VBE = 0.025 V

26. CE Amplifier
• From the output characteristic curve we
move up and down the load line to estimate
that as IB changes by ±5μA the
corresponding change in VCE is about –2.5
V. (Note the negative sign!)
• When iB =5μA, vCE = 3.75V; when iB =15μA,
vCE = 1.25V
∆VCE = - 2.5 V

27. CE Amplifier
• From the input curve we estimate that as I B
changes by ±5μA about the bias level of
10μA then the corresponding change in VBE
is about 0.025 V.
• When iB =5μA, vBE = 0.5875V; when iB
=15μA, vBE = 0.6125.
∆VBE = 0.025 V

28. CE AMPLIFIER
‘Operating’
or Q point set
by d.c. bias.

29. CE Amplifier
• The CE small signal (a.c.) voltage gain is
∆VCE - 2.5 V
= = −100
∆VBE 0.025 V

30. CE Amplifier
• From the output characteristic curve we also
see that as we move up and down the load
line a change in IB of ±5μA produces a
corresponding change in IC of ±5mA.
• The a.c. signal current gain is 100.
• This is consistent with the ideal
characteristic uniform line spacing, i.e. β =
100 = constant.

31. CE AMPLIFIER
‘Operating’
or Q point set
by d.c. bias.

32. Ideal CE Amplifier Summary
• The CE voltage and current gains are high
• The voltage gain is negative, i.e. the output
signal is inverted.
• The d.c. bias current sets the signal input
impedance of the transistor through the
dynamic resistance.
• IC = β IB ; iC = β iB.

33. Ideal CE Amplifier Summary
• Two of these statements:
• The d.c. bias current sets the signal input
impedance of the transistor through the
dynamic resistance.
• IC = β IB ; iC = β iB.
will be used to derive our simplified small
signal equivalent circuit of the BJT. (It is
simplified because it is based on ideal
BJTs)

34. Additional a.c. Load
• Suppose an a.c. coupled load RL = 2.5 kΩ is
added V CC
RC
vout
vin
C RL
GND

35. Additional a.c. Load
• The ‘battery’ supplying the d.c. supply VCC has
negligible impedance compared to the other
resistors, in particular RC.
• It therefore presents an effective ‘short-circuit’ for
a.c. signals.
• The effective a.c. load is the parallel combination
of RC and RL . (From the collector C we can go
through RC or RL to ground)

36. Additional a.c. load
a.c. short via
d.c. supply
RC
iC
RL
GND

37. Additional a.c. load
iC
RL RC
vce
GND

38. Additional a.c. Load
• We now need to construct an a.c. load line
on the output characteristic.
• This goes through the operating point Q and
has slope
1 1
− =− A/V
RC//RL 1250
• This is hard to draw!

39. Additional a.c. Load
a.c. load line,
drawn with
required slope
through Q
point.

40. Additional a.c. Load
• The available voltage swing and the voltage
gain are calculated using the a.c. loadline.
• Symmetric swing reduced to about ±1.25 V
• Voltage gain reduced to about –50.

41. Stabilised Bias Circuits
• These seek to fix the emitter current
independently of BJT parameter variations,
principally in β.
• This is best achieved by introducing an
emitter resistance and setting the base
voltage via a resistor network (R1, R2) which
acts as a potential divider (provided I B can
be assumed small)

42. Stabilised Bias Circuit
Bias bit of the circuit, a.c. source and load
capacitor coupled. RE is capacitor by-
passed (shorted) for a.c. signals
VCC
R1 RC
vout
RS
R2 RE
VS
GND

43. Stabilised Bias Circuit
• See handout for a detailed analysis of this
bias circuit
• We will also look at a worked example of a
transistor amplifier based on such a
stabilised bias circuit once we have
established an a.c. equivalent circuit for the
transistor.

44. Stabilised Bias Circuit
• Finally we give another circuit which
provides bias stability using negative
feedback from the collector voltage.
+VCC
RC
RB
IC
D.C collector voltage VC
IB
VBE =0.6 V
GND

45. Stabilised Bias Circuit
VC = VCC - IRC RC,
IRC = IB + IC = (1 + β )IB
+VCC
IRC RC
RB
IC D.C collector voltage VC
IB
VBE =0.6 V
GND

46. Stabilised Bias Circuit
VC = VBE + IB RB ≈ 0.6 + IB RB
+VCC
IRC
RC
RB
IC
D.C collector voltage VC
IB
VBE =0.6 V
GND

47. Stabilised Bias Circuit
• For example, increasing β, increases IC
which lowers the collector voltage V C and
hence and IB and IC
+VCC
RC
RB
IC
D.C collector voltage VC
IB
VBE =0.6 V
GND