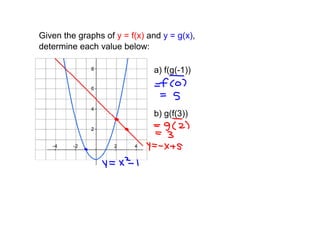
1. The document discusses composite functions, which involve combining two functions f(x) and g(x) where the output of one is used as the input of the other. It provides examples of evaluating composite functions using tables and graphs. 2. Key steps for evaluating composite functions are: 1) Substitute the inner function into the outer function and 2) Simplify the expression. Order matters as f(g(x)) and g(f(x)) may have different values. 3. Examples are worked through to find composite functions given basic functions like f(x) = x + 1 and g(x) = 2x as well as more complex rational functions.

1. Mental Math
1. If f(x) = √x - 2 and g(x) = x2, find the domain of f(x) g(x)..
3. Write the equation of the horizontal asymptote for f(x) =
x + 5
2x - 1
2. Given that h(x) = 3x3 - x + 5 and that h(x) = f(x) - g(x),
determine f(x) and g(x).
4. The graph of a rational function, f(x), has an asymptote
Write a possible equation for f(x).
when x = 0 and a point of discontinuity when x = 1.

2. Composite Functions
Refers to the combining of two functions f(x) and g(x)
where the output of one function is used as the input of the
other function.
Recall, f(x) = 2x - 1 find f(3)
x = 3
The notation used for compostion is
(f ◦ g)(x) = f(g(x))
Inner brackets are done first.
First substitute into g, then into f.
Reads "f composed with g of x" or "f of g of x"

3. Ex. The tables below define two functions.
Use these tables to determine each value below.
x g(x)
-2 3
-1 2
0 1
1 0
2 -1
x f(x)
-2 8
-1 3
0 0
1 -1
2 0
a) f(g(-1))
b) f(f(2))
c) g(f(1))
d) g(g(2))

4. Given the graphs of y = f(x) and y = g(x),
determine each value below:
a) f(g(-1))
b) g(f(3))

5. Ex) If f(x) = 4x, g(x) = x + 6, and h(x) = x2, find
a) f(g(3))
b) g(h(-2))
c) h(h(2))

6. Ex 1) If f(x) = x + 1 and g(x) = 2x, find (f ◦ g)(x).
Steps:
1) Write the expression for
the function of g(2x) in the
g(x) 'spot' in the composition
2) Now substitute this
expression (2x) into function f
in the x 'spot'
3) Simplify (if necessary)
Composite Functions

7. Ex 2) Given f(x) = 5x and g(x) = x2 + 1, find
a) (f ◦ g)(x)
b) (g ◦ f)(x)
Notice that (f ◦ g)(x) and (g ◦ f)(x) do not
necessarily have the same answer.

8. Ex 3) Given f(x) = x2 and g(x) = x + 3, find
a) f(g(x))
b) g(f(x))
c) f(f(x))
d) g(g(x))
and state the domain.