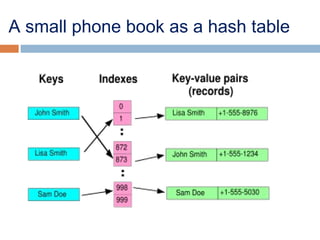
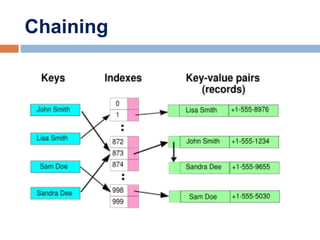
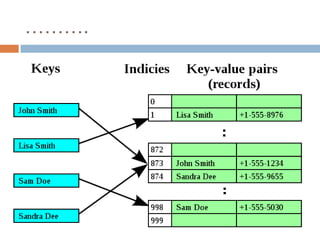
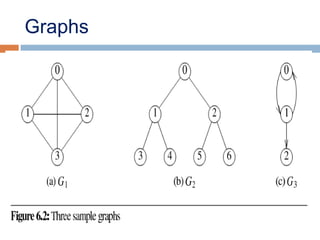
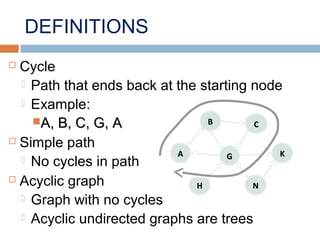
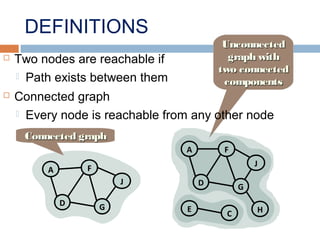
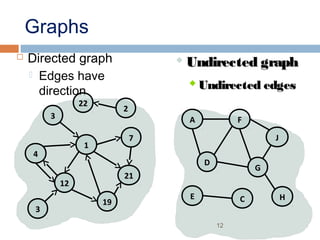
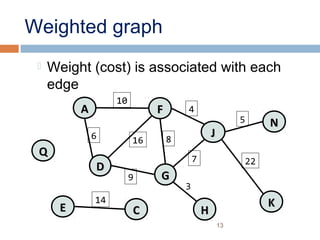
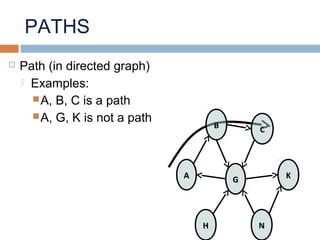
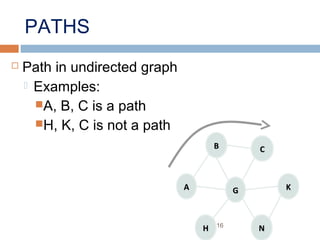
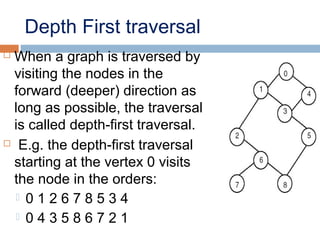
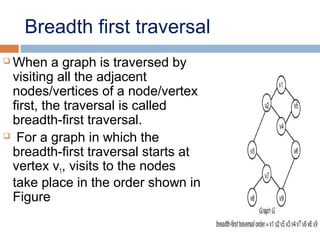
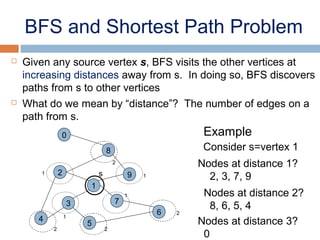
This document provides definitions and concepts related to graphs. It defines a graph as a data structure consisting of vertices and edges linking vertices, which can represent objects and relationships. Graphs are a generalization of trees that allow any type of relationship between nodes. Common graph representations include adjacency lists and matrices. The document also discusses graph traversal methods, minimum spanning trees, and applications of graphs.









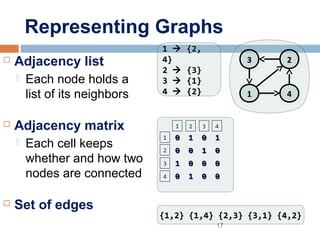
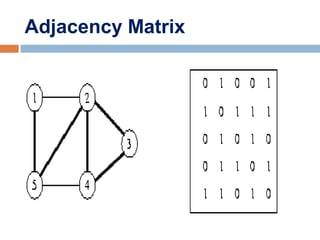
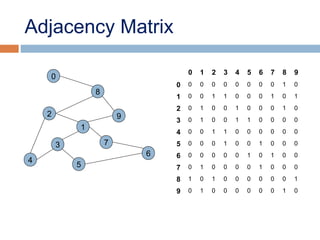
![Adjacency Matrix
• 2D array, where n is the number of vertices in the graph
• Each row and column is indexed by the vertex id.
- e,g a=0, b=1, c=2, d=3, e=4
• An array entry A [i] [j] is equal to 1 if there is an edge
connecting
vertices i and j. Otherwise, A [i] [j] is 0.](https://image.slidesharecdn.com/lecture5bgraphsandhashing-140719095221-phpapp02/85/Lecture-5b-graphs-and-hashing-18-320.jpg)
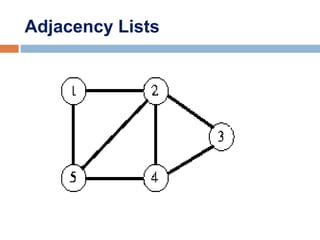
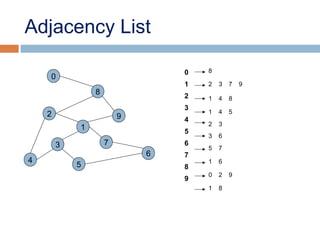
![Adjacency List
• The adjacency list is an array A[0..n-1] of lists, where n is the
number of vertices in the graph.
•Each array entry is indexed by the vertex id (as with adjacency
matrix)
• The list A[i] stores the ids of the vertices adjacent to i.](https://image.slidesharecdn.com/lecture5bgraphsandhashing-140719095221-phpapp02/85/Lecture-5b-graphs-and-hashing-21-320.jpg)








![Representing Graphs in C#
public class Graphpublic class Graph
{{
int[][] childNodes;int[][] childNodes;
public Graph(int[][] nodes)public Graph(int[][] nodes)
{{
this.childNodes = nodes;this.childNodes = nodes;
}}
}}
Graph g = new Graph(new int[][] {Graph g = new Graph(new int[][] {
new int[] {3, 6}, // successors of vertice 0new int[] {3, 6}, // successors of vertice 0
new int[] {2, 3, 4, 5, 6}, // successors of vertice 1new int[] {2, 3, 4, 5, 6}, // successors of vertice 1
new int[] {1, 4, 5}, // successors of vertice 2new int[] {1, 4, 5}, // successors of vertice 2
new int[] {0, 1, 5}, // successors of vertice 3new int[] {0, 1, 5}, // successors of vertice 3
new int[] {1, 2, 6}, // successors of vertice 4new int[] {1, 2, 6}, // successors of vertice 4
new int[] {1, 2, 3}, // successors of vertice 5new int[] {1, 2, 3}, // successors of vertice 5
new int[] {0, 1, 4} // successors of vertice 6new int[] {0, 1, 4} // successors of vertice 6
});});
00
66
44
11
55
22
33](https://image.slidesharecdn.com/lecture5bgraphsandhashing-140719095221-phpapp02/85/Lecture-5b-graphs-and-hashing-35-320.jpg)
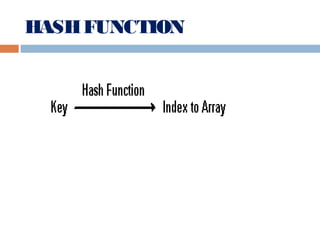
![HASH TABLES - INTRODUCTION
WHY the use of Hash tables
Hash tables are good for doing a quick
search on things.
For instance if we have an array full of data
(say 100 items). If we knew the position that a
specific item is stored in an array, then we
could quickly access it.
For instance, we just happen to know that the
item we want is at position 3; I can apply:
myitem=myarray[3];](https://image.slidesharecdn.com/lecture5bgraphsandhashing-140719095221-phpapp02/85/Lecture-5b-graphs-and-hashing-36-320.jpg)