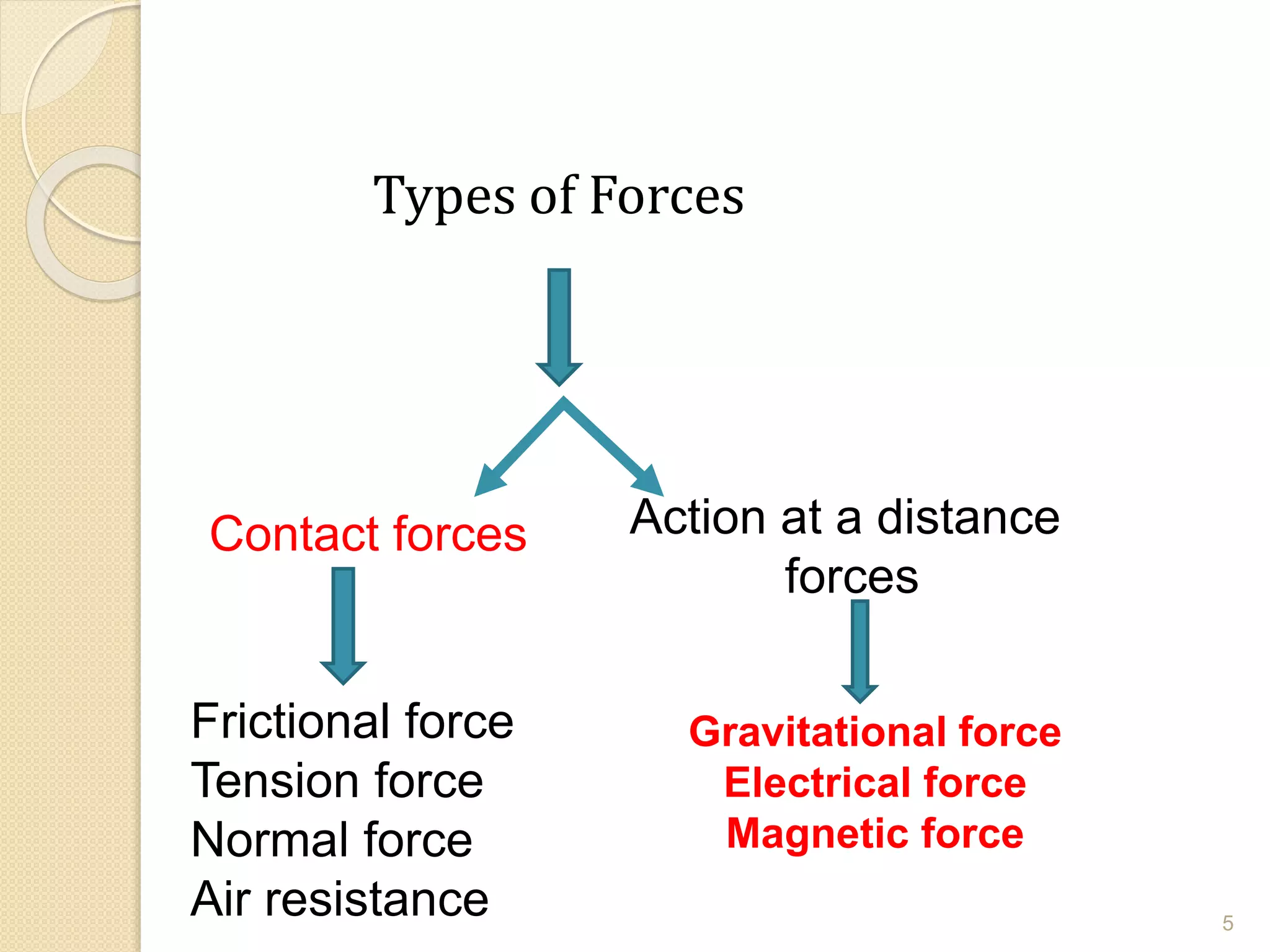
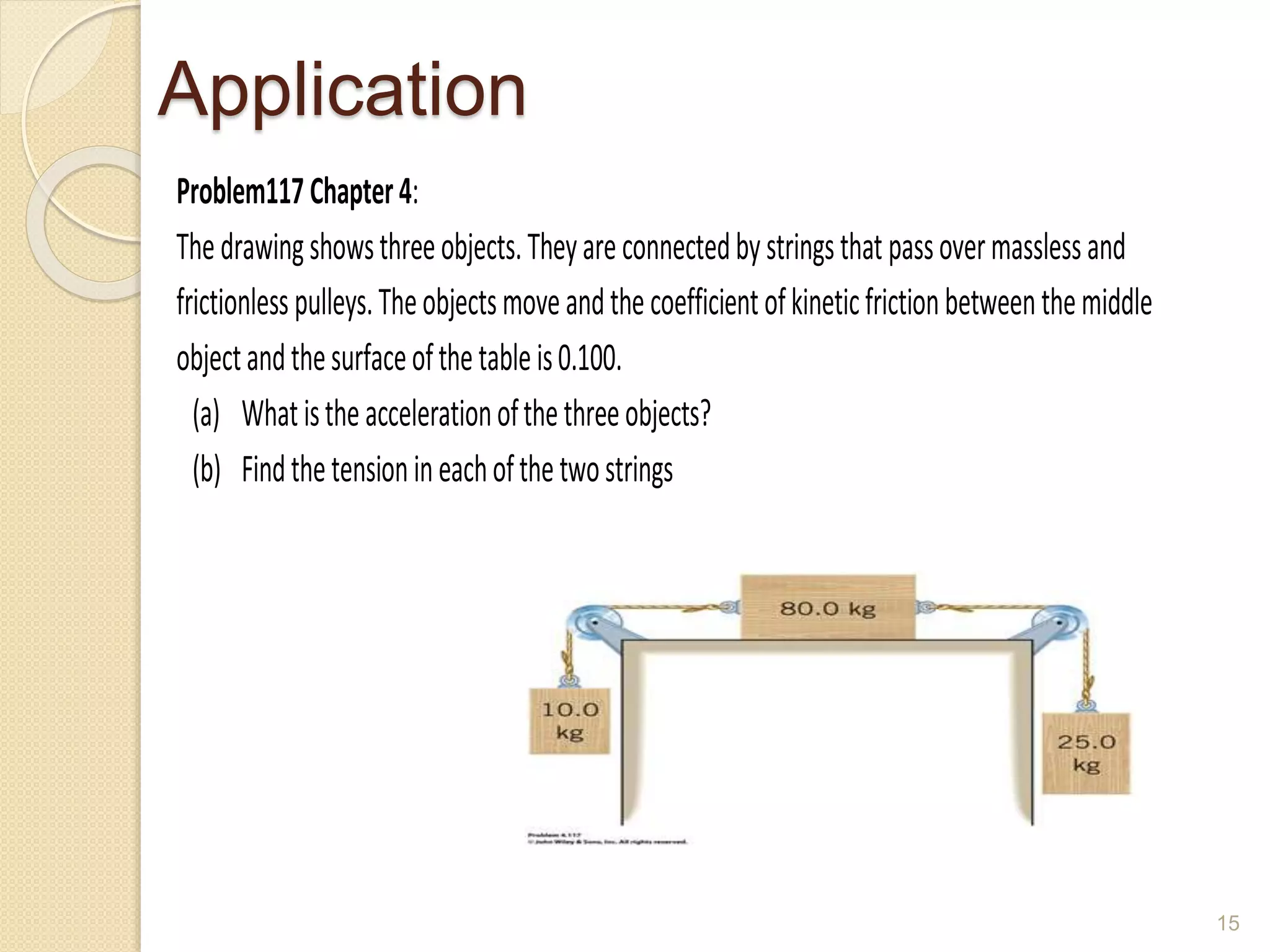
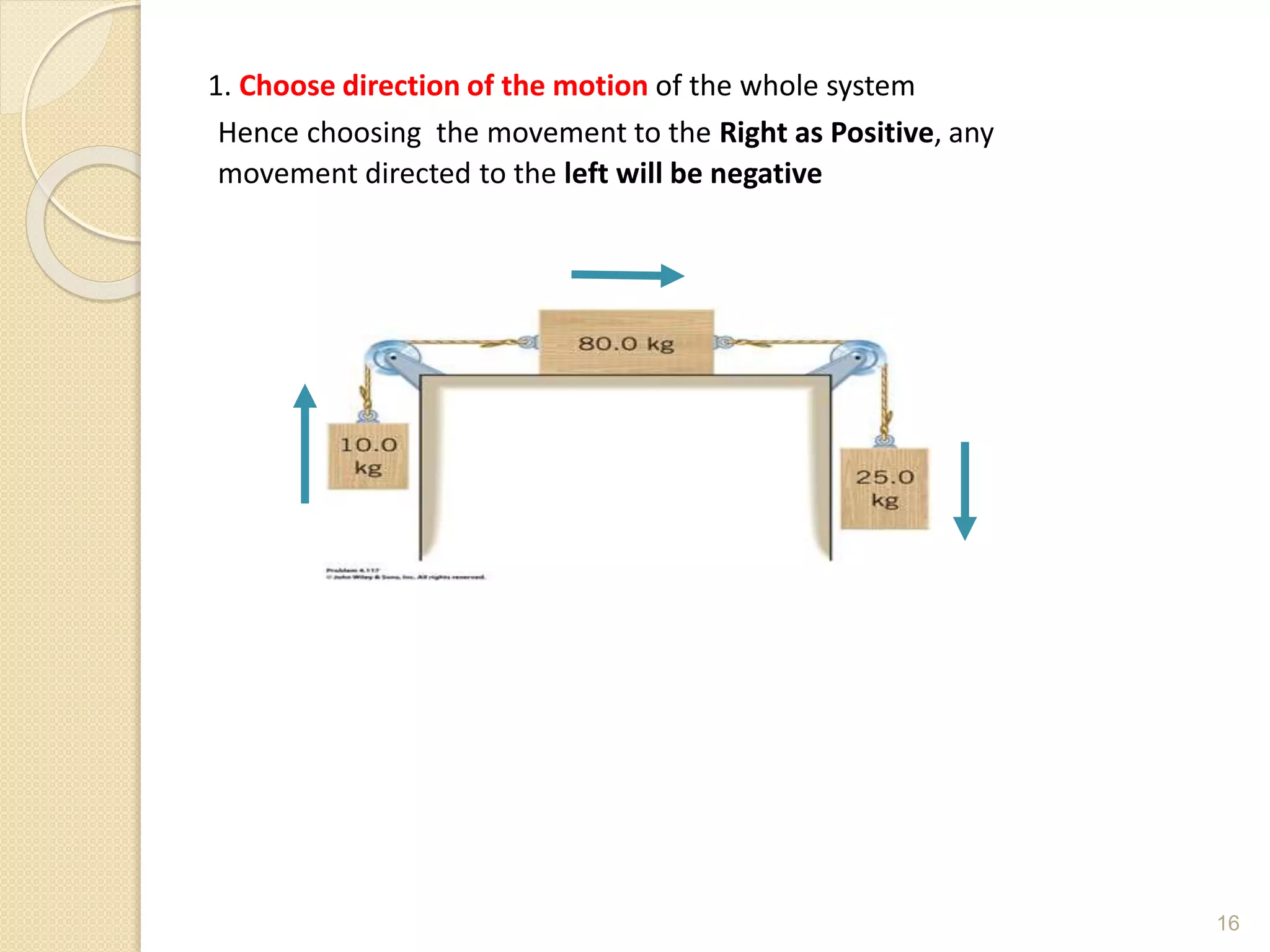
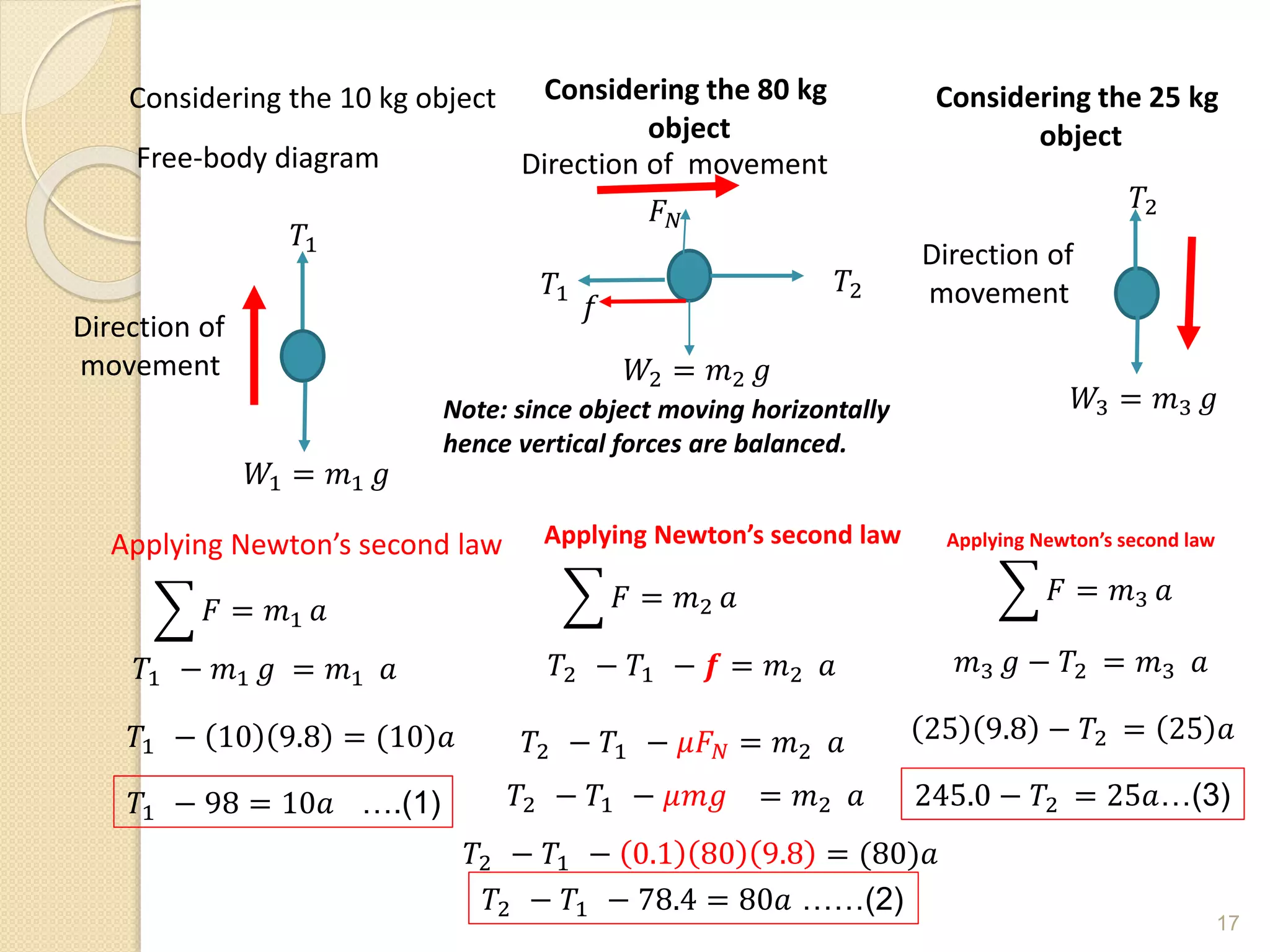
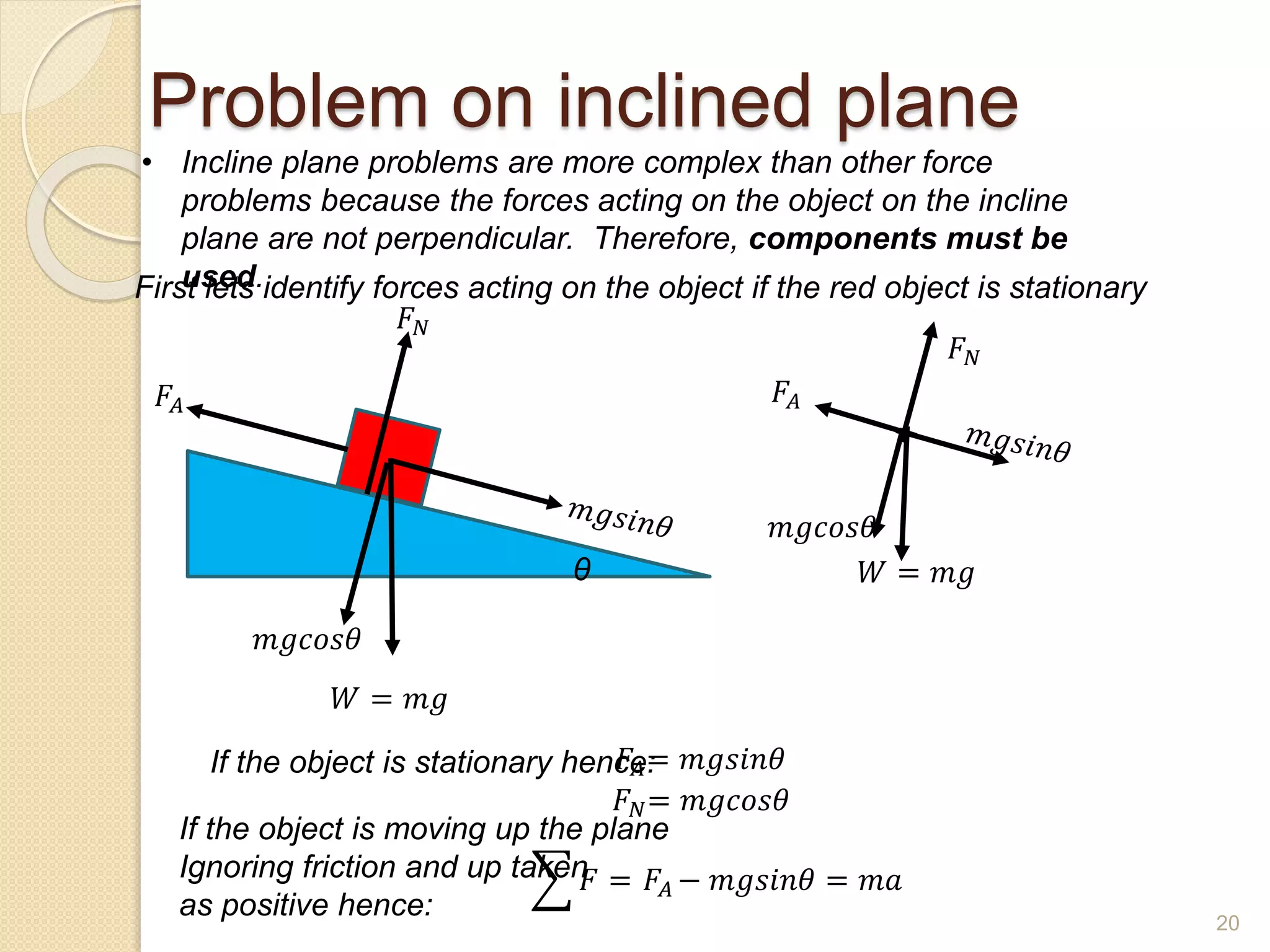
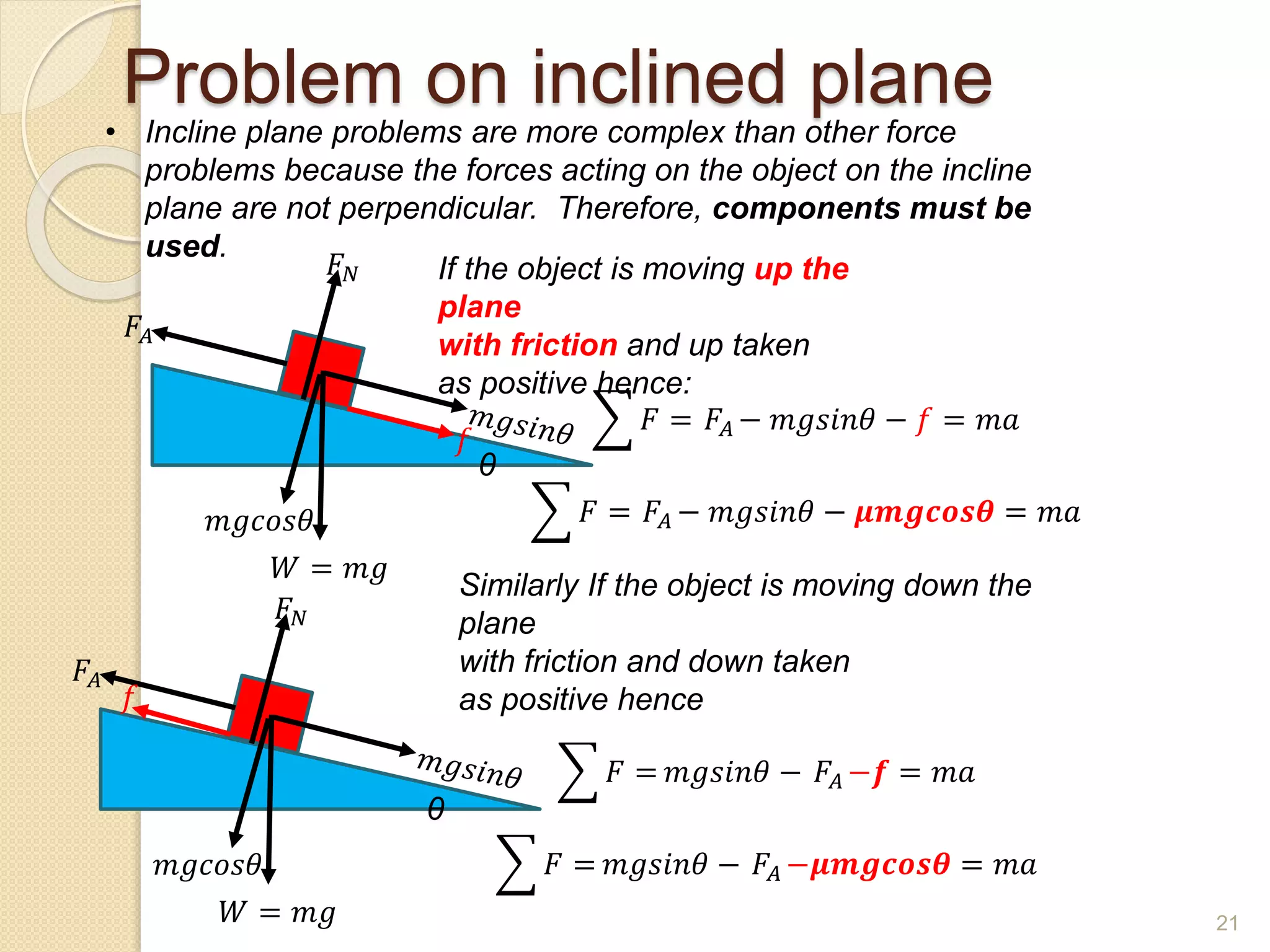
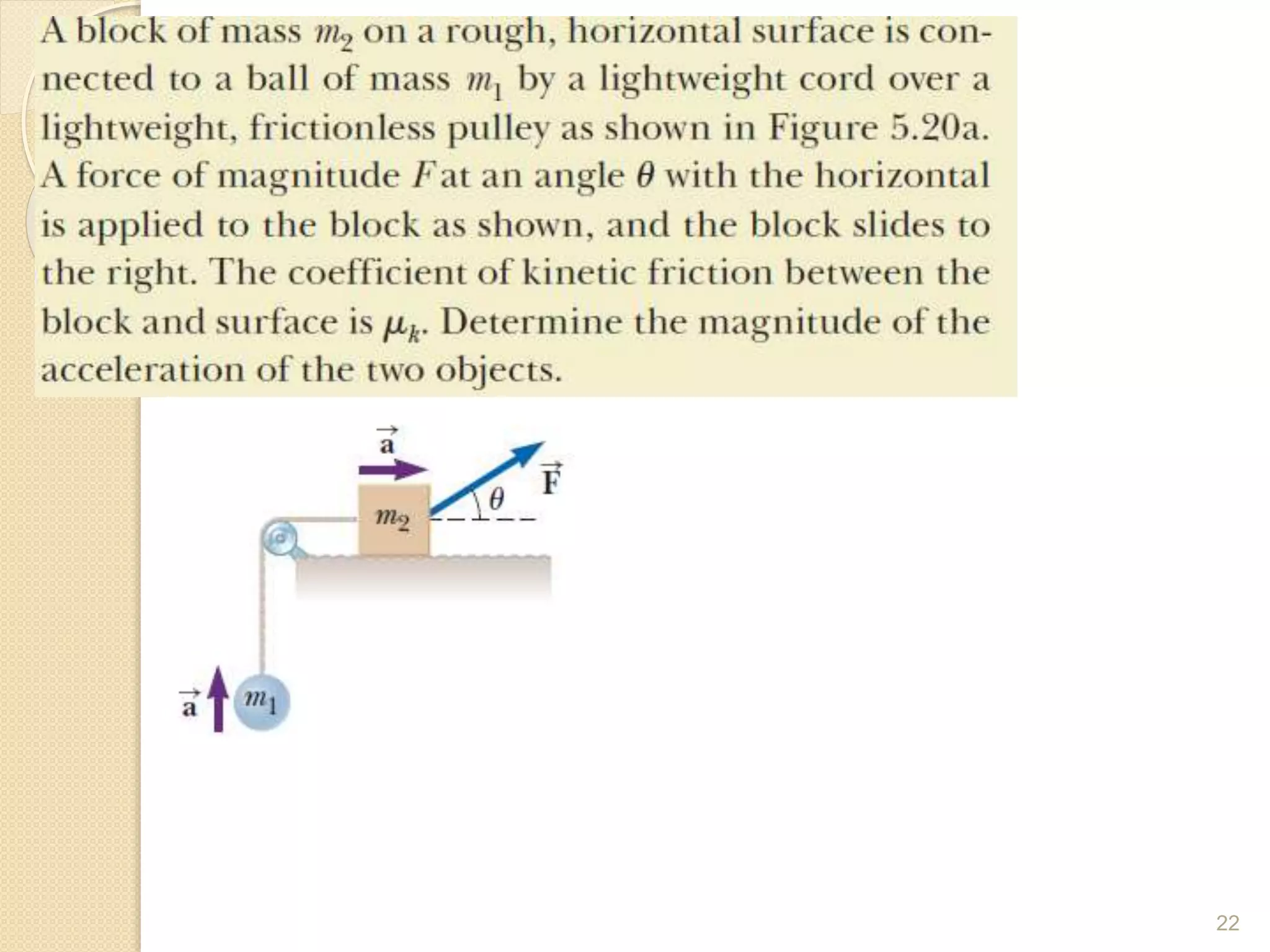
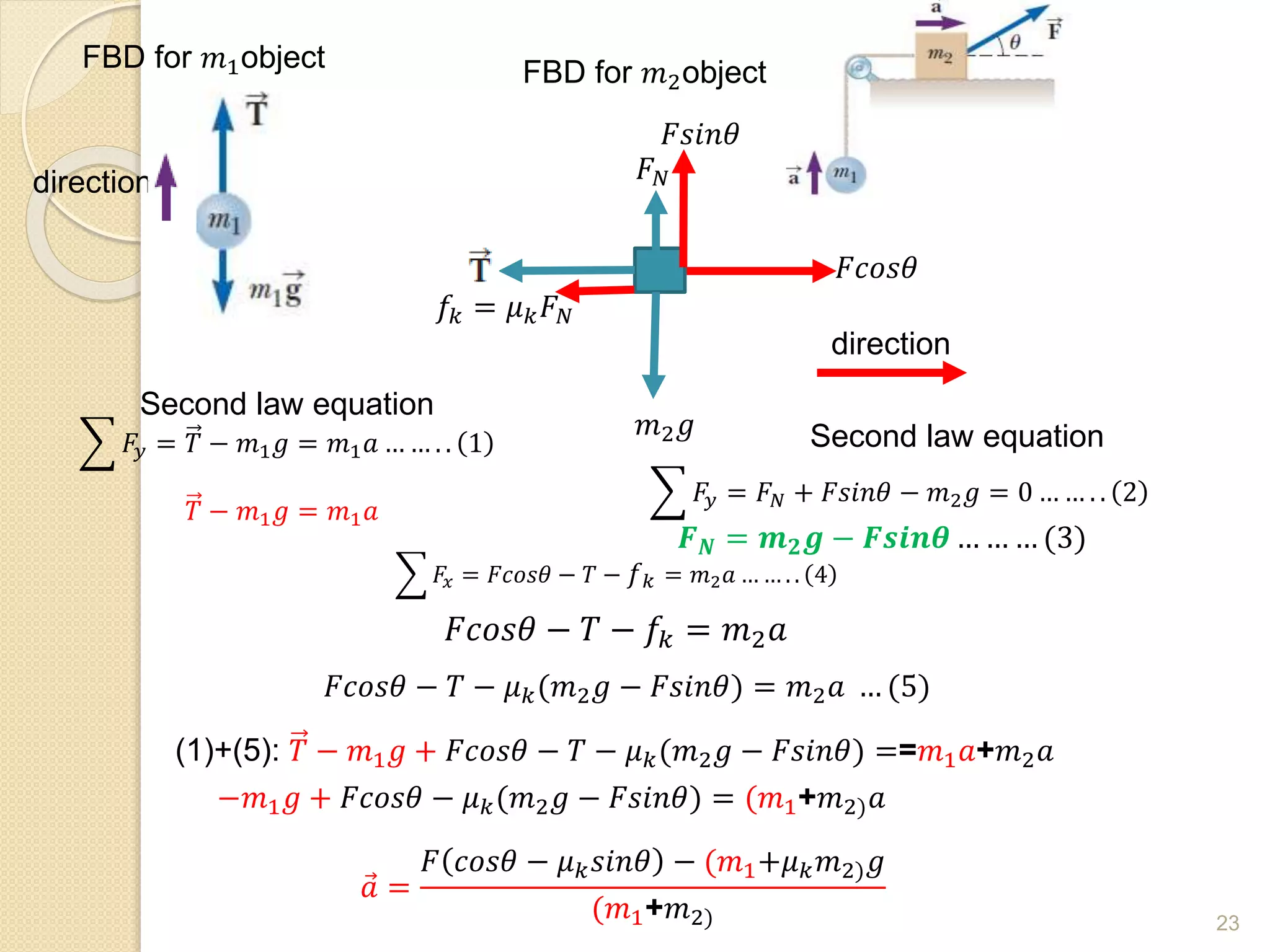
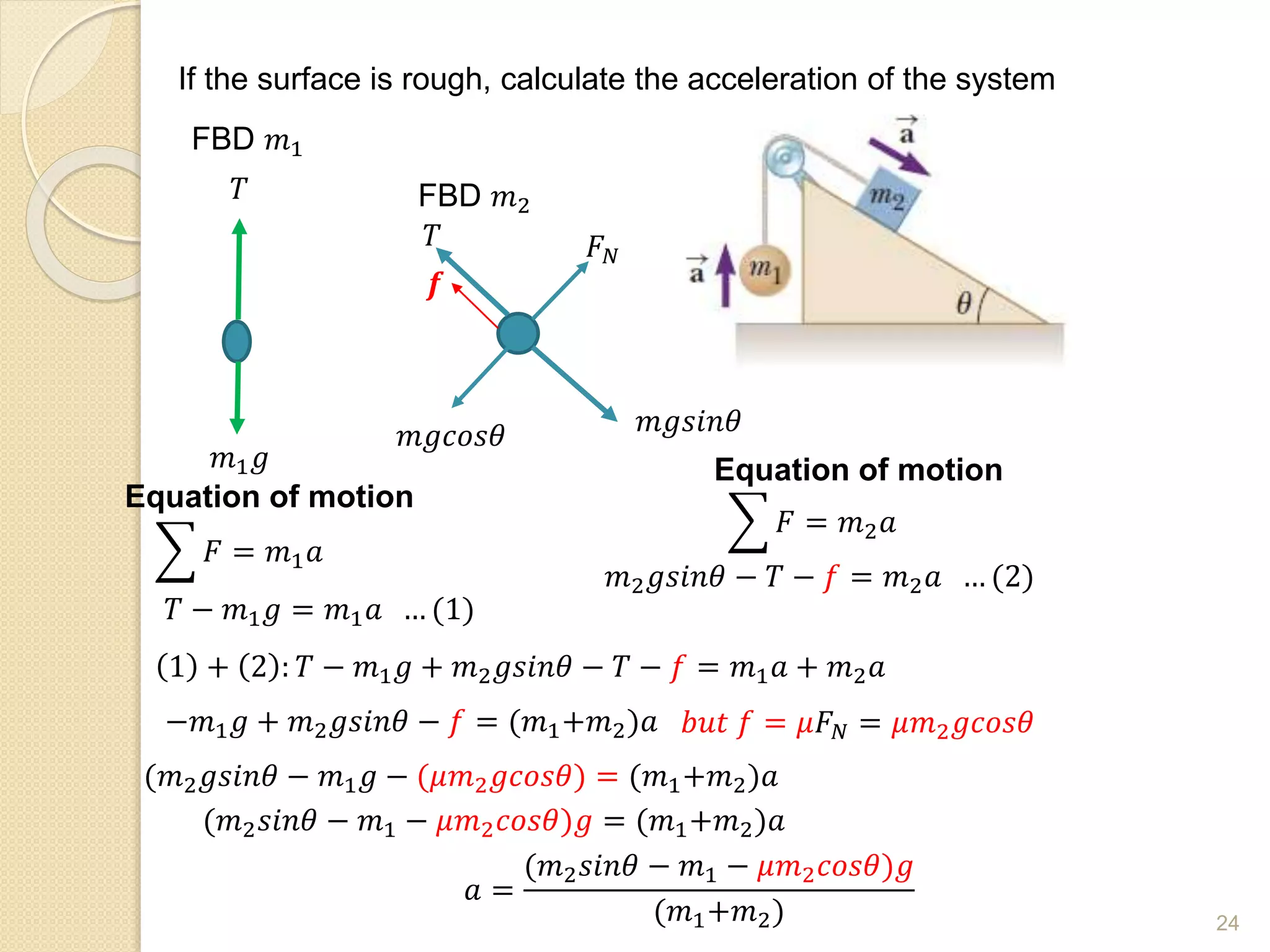
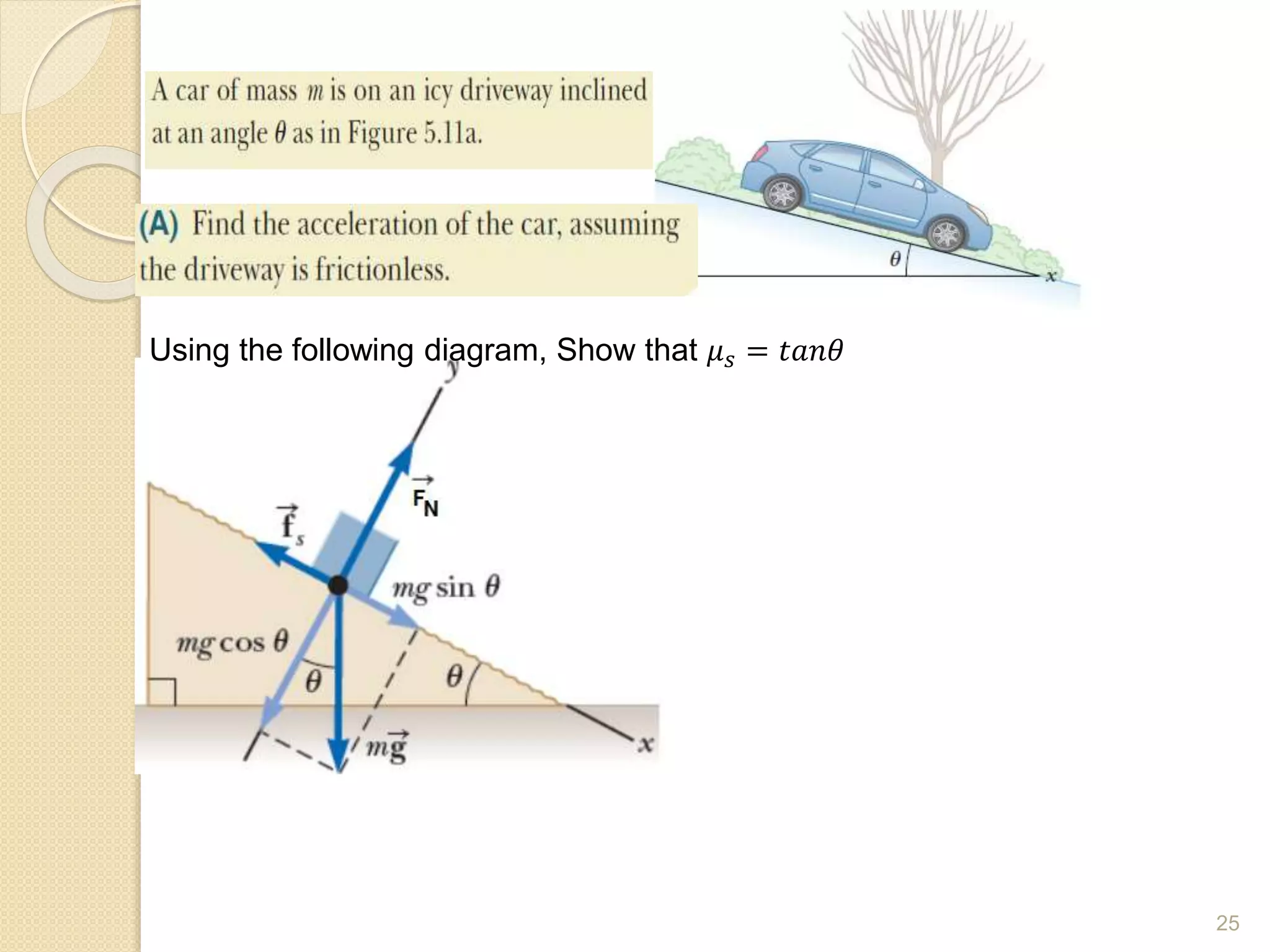
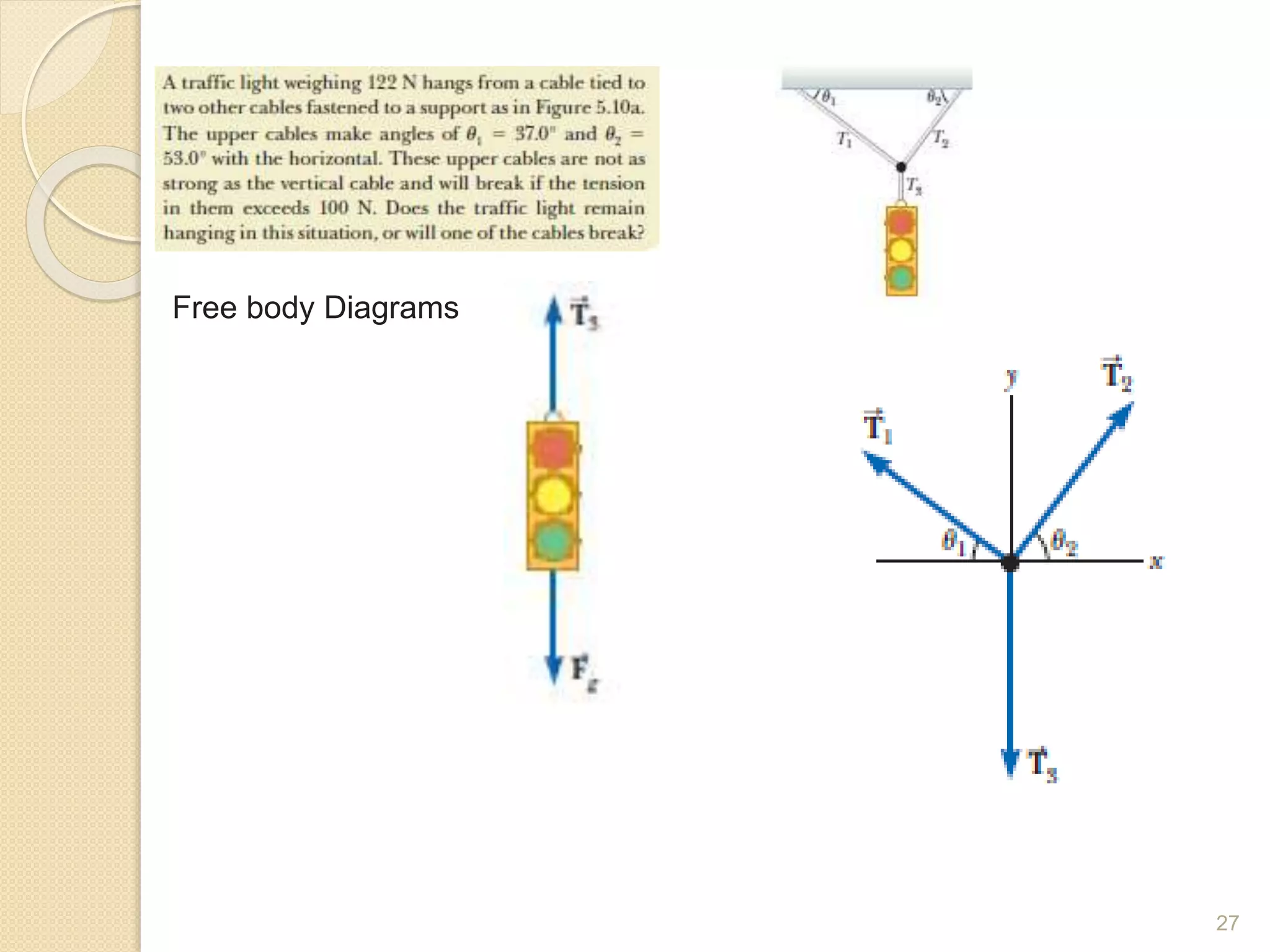
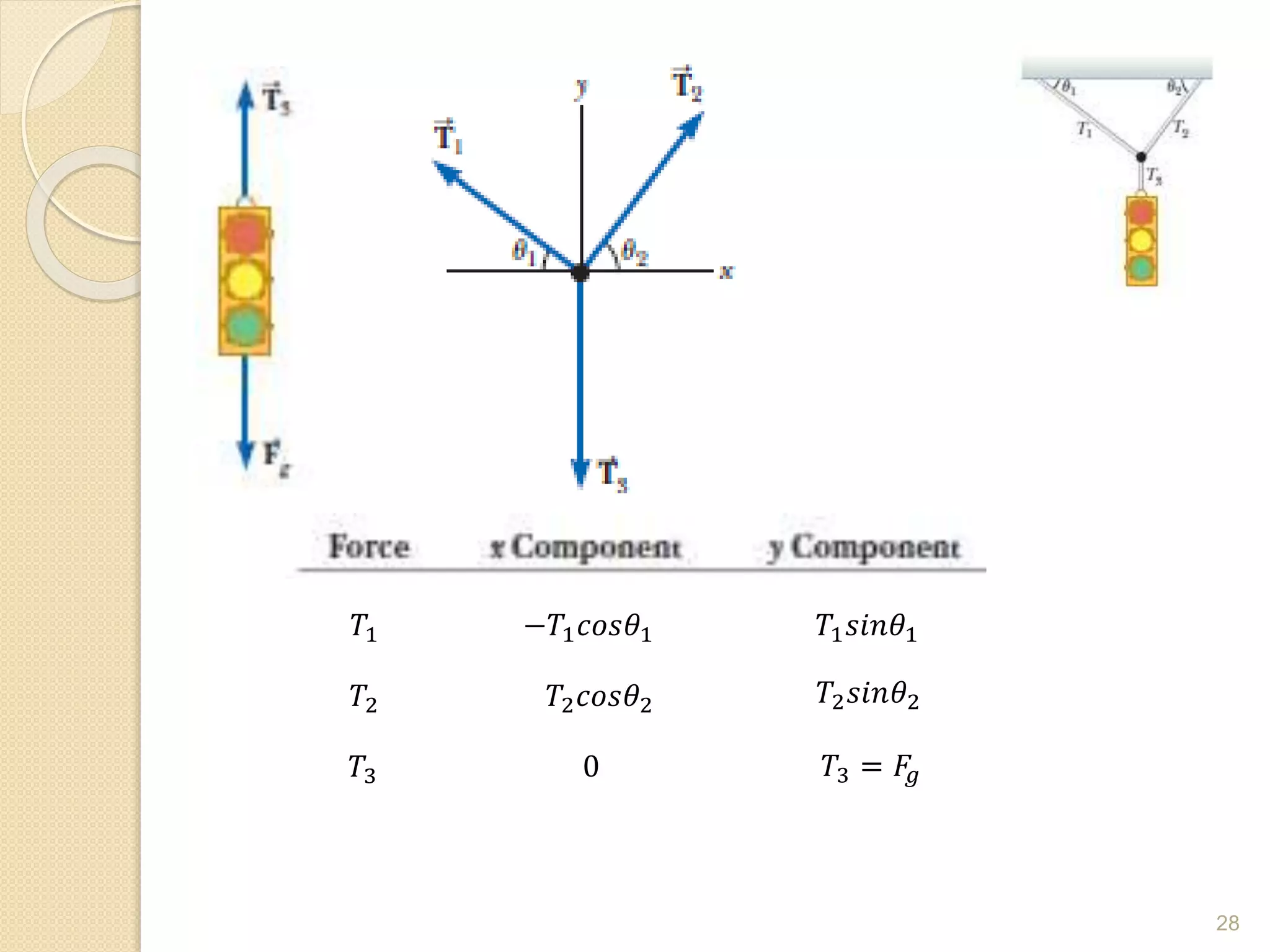
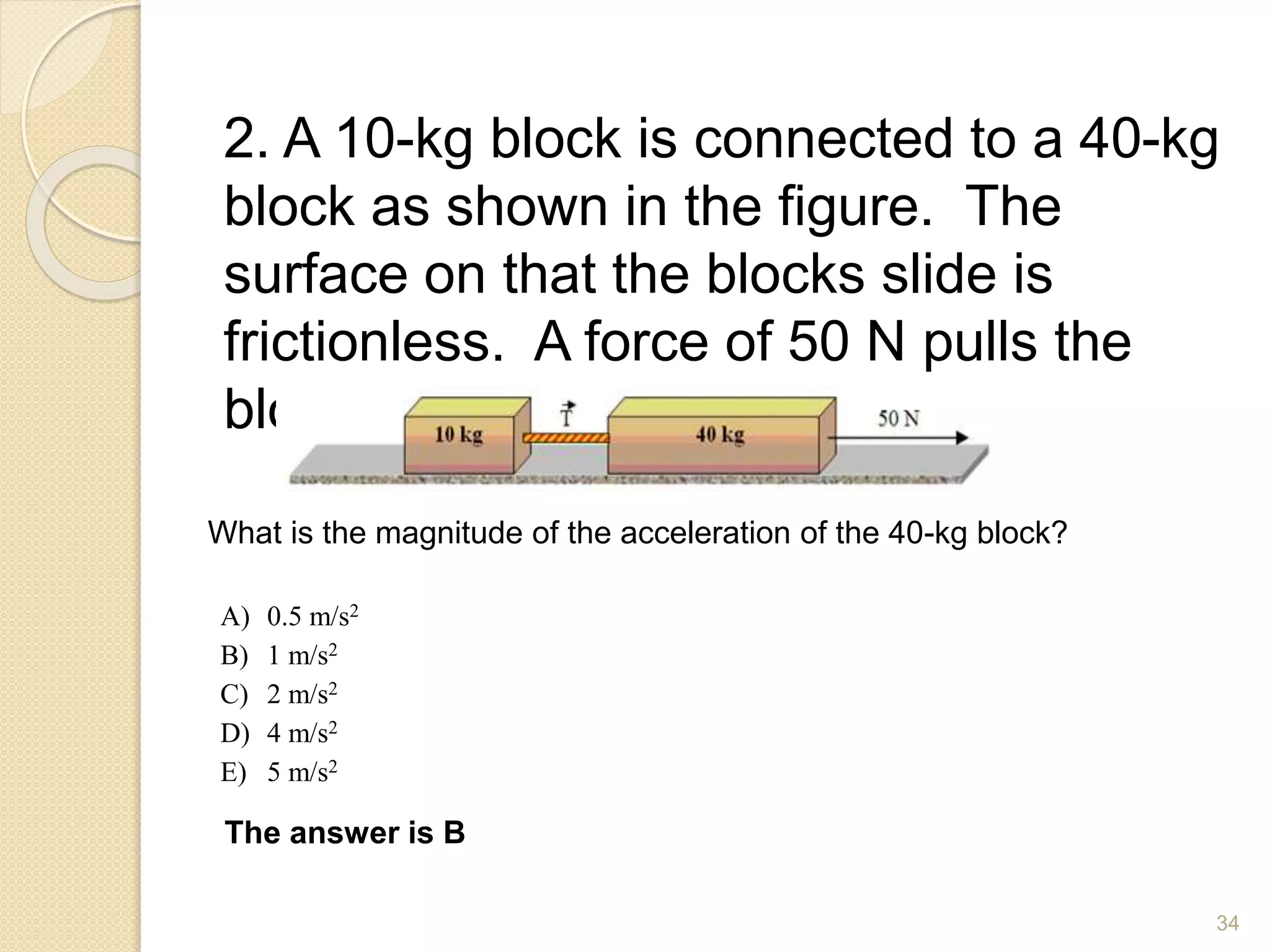
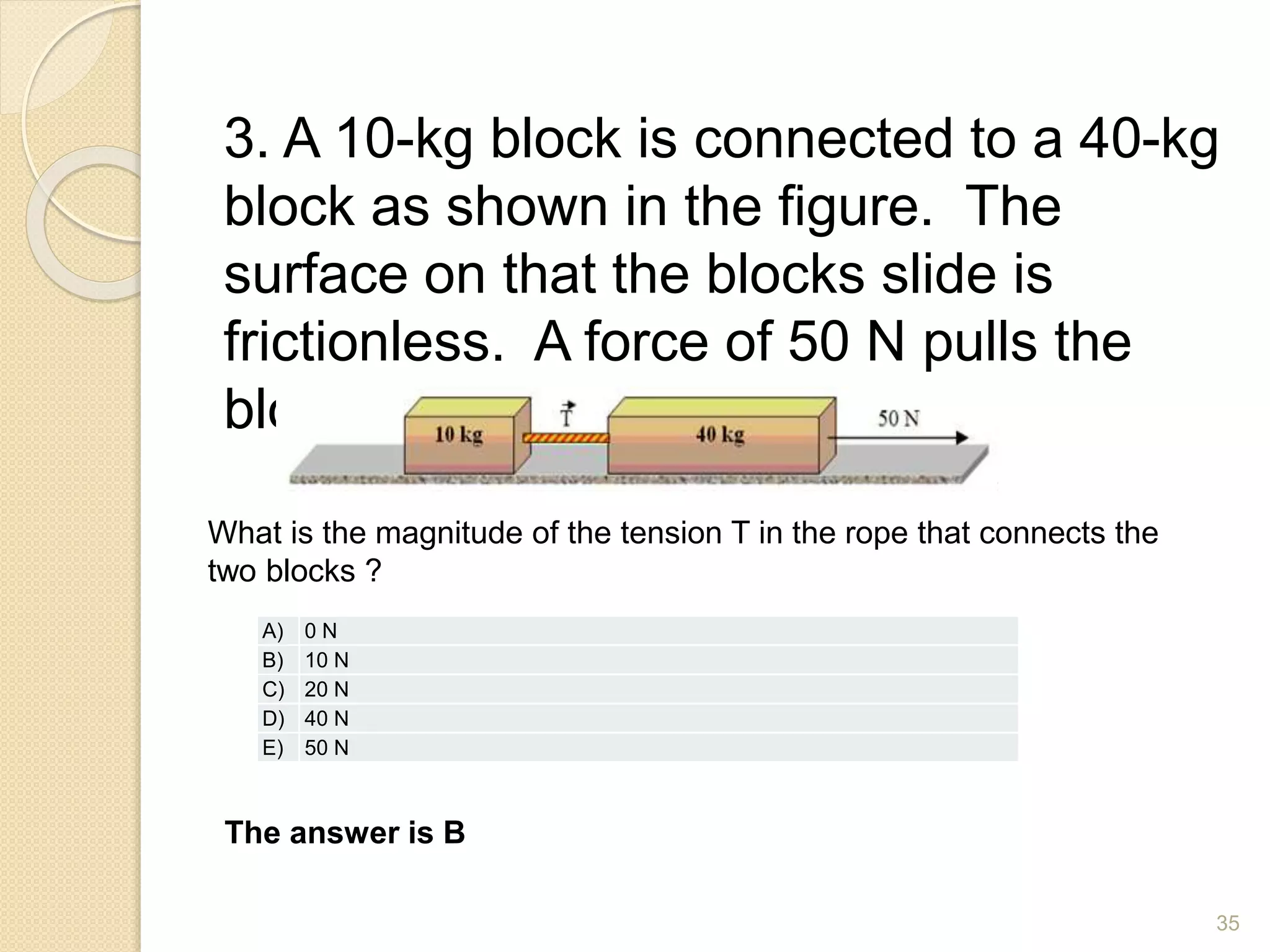
This document discusses Newton's laws of motion and their applications. It contains examples of problems involving Newton's first law regarding inertia and an object's motion when the net force is zero. Newton's second law relating force, mass and acceleration is explained. Free body diagrams are demonstrated as a problem solving tool. Examples are provided of calculating acceleration from forces using Newton's second law for objects on an inclined plane and connected objects on pulleys. Friction forces are also discussed.

1. Newton’s laws of motion
Applications
23 April 2021
Compiled by Mphiriseni Khwanda
University of Johannesburg
1

2. Questions
What happens to the speed if the net
force is constant
 A: The speed Changes
 B: The speed decreases
 C: The speed increases
 D:The speed is constant
Use PhET to verify
2

3. Questions
What happens to the speed if the net
force is zero
 A: The speed Changes
 B: The speed decreases
 C: The speed increases
 The speed is constant
Use PhET to verify
3

4. Impact of net force/resultant
force
 It can cause the change in state
of motion
 It can cause work to be done on
an object
 Is proportional to the rate of
change in momentum
 When the net force causes a
change in the state of motion
and /or direction. We say the
object is accelerating.
 Technically: The net force causes
an acceleration
4

5. Types of Forces
Contact forces Action at a distance
forces
Frictional force
Tension force
Normal force
Air resistance
Gravitational force
Electrical force
Magnetic force
5

6. Misconceptions about newton’s first law
 Newton's first law of motion declares that a force is not
needed to keep an object in motion.
 Slide a book across a table and watch it slide to a rest
position.
 The book in motion on the table top does not come to a
rest position because of the absence of a force; rather it
is the presence of a force - that force being the force
of friction - that brings the book to a rest position.
 In the absence of a force of friction, the book would
continue in motion with the same speed and direction -
forever (or at least to the end of the table top)!
 A force is not required to keep a moving book in
motion
6

7. Static and kinetic friction
When the two surfaces are not sliding
across one another the friction is called
static friction .
𝝁𝑺 is called the coefficient of static friction.
𝒇𝑺 is called the static frictional force.
𝑭𝑵 is called the normal force which is always
perpendicular to the surface.
N
s
MAX
s F
f 

When the two surfaces are sliding across
one another the friction is called kinetic
friction.
𝝁𝑲 is called the coefficient of kinetic friction.
N
k
k F
f 

NOTE:
The frictional force is always in the opposite direction of the
motion
7

8. Statement of Newton’s first law and inertia
 Every object will remain at rest or
continue moving with uniform motion
in a straight line unless acted upon by
the unbalanced forces
 The continuous state of motion is
maintained by INERTIA
 Inertia is the property of matter that
requires the unbalanced force (non-
zero net force) to change its state of
motion
8

9. Newton’s First Law
Forces are balanced
Resultant force 𝐹 = 0 𝑁
acceleration 𝑎 = 0 𝑚 𝑠−2
Objects at rest Objects in uniform motion
Stay at rest Stay in uniform motion
Same speed & direction
𝑉 = 0 𝑚/𝑠
𝑉 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 ≠ 0 𝑚/𝑠
What happens to acceleration
when forces are balanced?
What happens to the motion of an
Object when acceleration is zero?
9

10. The Statement of Newton’s second
law
 The acceleration of an object is directly proportional to
the resultant force acting on an object, the object’s
acceleration should be in the same direction as the
resultant force
 Mathematically the relation can be expressed as:
𝐹 = 𝑚𝑎
NOTE:
 The acceleration depends on force and not the other
way round.
 In other words, you cannot increase acceleration in
order to increase a force or mass
 The resultant force or net force is not a SINGLE
force but the SUM of all the forces acting on the object
that is responsible for acceleration
10

11. Newton’s Second Law
Forces are unbalanced
Resultant force 𝐹 ≠ 0 𝑁
There is acceleration 𝑎 = constant ≠ 0 𝑚 𝑠−2
An object changes its state of motion
It changes its velocity (increases or decreases)
OR /and
changes its direction
Directly proportional
to the Resultant Force
11

12. Free-Body Diagrams
1. A free body diagram is a diagram that shows all
of the forces acting on an object.
2. There are five different ways to draw free body
diagrams: horizontal, vertical, incline plane,
free fall, and tension.
3. Gravity’s effect on an object represented by
weight
4. The normal force is the force perpendicular to
the surface
12

13. Problem Solving Strategies: Newton’s Second Law
1. Draw a Free-Body Diagram for each object.
2. Choose the direction of motion of the system
3. Identify if there is a friction and label the friction force
immediately because one can easily forget it.
4. Note that frictional force 𝒇 = 𝝁𝑭𝑵 = 𝝁𝒎𝒈 =𝝁𝒎𝒈𝒄𝒐𝒔𝜽
𝒐𝒏 𝒊𝒏𝒄𝒍𝒊𝒏𝒆𝒅 𝒑𝒐𝒔𝒊𝒕𝒊𝒐𝒏
5. Also check weight and label it immediately, it can be easily
forgotten.
6. Choose the direction of the motion: for example if towards the
right is positive, hence all vectors pointing to the right will be
positive and to the left negative.
7. For each object, apply Newton’s second law to formulate an
equation and label the equation 1, 2 etc. for example, object 1:
𝑭 = 𝒎𝟏𝒂 and for object 2: 𝑭 = 𝒎𝟐𝒂 etc.
8. Note that if objects are attached by strings all will have the
same acceleration.
9. Solve the equations simultaneously for unknowns
10. As a hint, adding equations might eliminate the tensions and
help you to calculate acceleration first.
13

14. Your Turn
1. Draw a free body diagram of a 10 kg
rock as it is lifted straight up with a
constant force of 148 N. Calculate
the net force acting on the rock and
its acceleration.
2. An 8000 kg Navy jet is accelerating
upward at 4 m/s2. Calculate the
upward force provided by the jet’s
engines to achieve this acceleration
14

15. Application
Problem117Chapter4:
Thedrawingshowsthreeobjects.Theyareconnectedbystringsthatpassovermasslessand
frictionlesspulleys.Theobjectsmoveandthecoefficientofkineticfrictionbetweenthemiddle
objectandthesurfaceofthetableis0.100.
(a) Whatistheaccelerationofthethreeobjects?
(b) Findthetensionineachofthetwostrings
15

16. 1. Choose direction of the motion of the whole system
Hence choosing the movement to the Right as Positive, any
movement directed to the left will be negative
16

17. Considering the 10 kg object
Free-body diagram
Direction of
movement
𝑇1 − 𝑚1 𝑔 = 𝑚1 𝑎
𝑇1
𝑊1 = 𝑚1 𝑔
Applying Newton’s second law
𝐹 = 𝑚1 𝑎
𝑇1 − 10 9.8 = (10)𝑎
𝑇1 − 98 = 10𝑎 ….(1)
Considering the 80 kg
object
𝑇1
𝑓
𝑇2
Direction of movement
Note: since object moving horizontally
hence vertical forces are balanced.
Applying Newton’s second law
𝐹 = 𝑚2 𝑎
𝑇2 − 𝑇1 − 𝒇 = 𝑚2 𝑎
𝑇2 − 𝑇1 − 𝜇𝐹𝑁 = 𝑚2 𝑎
𝑇2 − 𝑇1 − 𝜇𝑚𝑔 = 𝑚2 𝑎
𝑇2 − 𝑇1 − 0.1 80 9.8 = (80)𝑎
𝑇2 − 𝑇1 − 78.4 = 80𝑎 ……(2)
Considering the 25 kg
object
𝑊2 = 𝑚2 𝑔
𝑇2
Direction of
movement
Applying Newton’s second law
𝐹 = 𝑚3 𝑎
𝑚3 𝑔 − 𝑇2 = 𝑚3 𝑎
25 9.8 − 𝑇2 = 25 𝑎
245.0 − 𝑇2 = 25𝑎…(3)
𝐹𝑁
𝑊3 = 𝑚3 𝑔
17

18. We are left with mathematics, we have three equations and three unknowns
The equations
𝑇1 − 98 = 10𝑎 ….(1)
𝑇2 − 𝑇1 − 78.4 = 80𝑎 ……(2)
245.0 − 𝑇2 = 25𝑎…(3)
(1)+(2)+(3): 𝑇1 − 98 + 𝑻𝟐 − 𝑻𝟏 − 𝟕𝟖. 𝟒 + 𝟐𝟒𝟓. 𝟎 − 𝑻𝟐 = 10𝑎 +𝟖𝟎𝒂 +25𝑎
68.6 = 115𝑎
𝑎 = 0. 6 𝑚𝑠−2
Substituting a in (1) we get 𝑇1 − 98 = 10(0.6) 𝑇1 − 98 = 6 𝑇1 = 104 𝑁
Substituting a in (3) we get
245.0 − 𝑇2 = 25(0.6) 245.0 − 𝑇2 = 15 𝑇2 = 230.4 𝑁
18

19. Problem 116 Chapter 4:
As the diagram shows, two blocks are connected by a rope that pass over a set of pulleys. One block
has a weight of 412 N, and the other has a weight of 908 N. The rope and the pulleys are massless
and there is no friction.
(a) What is the acceleration of the lighter block?
(b) Suppose that the heavier block is removed, and a downward force of 908 N is provided by
someone pulling on the rope as part b of the drawing shows. Find the acceleration of the
remaining block.
(c) Explain why the answer in (a) and (b) are different.
19

20. Problem on inclined plane
• Incline plane problems are more complex than other force
problems because the forces acting on the object on the incline
plane are not perpendicular. Therefore, components must be
used.
θ 𝑊 = 𝑚𝑔
𝑚𝑔𝑐𝑜𝑠𝜃
𝐹𝐴
𝐹𝑁
First lets identify forces acting on the object if the red object is stationary
𝑊 = 𝑚𝑔
𝑚𝑔𝑐𝑜𝑠𝜃
𝐹𝑁
𝐹𝐴
If the object is stationary hence:
𝐹𝐴= 𝑚𝑔𝑠𝑖𝑛𝜃
𝐹𝑁= 𝑚𝑔𝑐𝑜𝑠𝜃
If the object is moving up the plane
Ignoring friction and up taken
as positive hence:
𝐹 = 𝐹𝐴 − 𝑚𝑔𝑠𝑖𝑛𝜃 = 𝑚𝑎
20

21. Problem on inclined plane
• Incline plane problems are more complex than other force
problems because the forces acting on the object on the incline
plane are not perpendicular. Therefore, components must be
used.
θ
𝑚𝑔𝑐𝑜𝑠𝜃
𝐹𝐴
𝐹𝑁
𝑊 = 𝑚𝑔
If the object is moving up the
plane
with friction and up taken
as positive hence:
𝐹 = 𝐹𝐴 − 𝑚𝑔𝑠𝑖𝑛𝜃 − 𝑓 = 𝑚𝑎
𝐹 = 𝐹𝐴 − 𝑚𝑔𝑠𝑖𝑛𝜃 − 𝝁𝒎𝒈𝒄𝒐𝒔𝜽 = 𝑚𝑎
Similarly If the object is moving down the
plane
with friction and down taken
as positive hence
𝐹 = 𝑚𝑔𝑠𝑖𝑛𝜃 − 𝐹𝐴 −𝒇 = 𝑚𝑎
𝐹 = 𝑚𝑔𝑠𝑖𝑛𝜃 − 𝐹𝐴 −𝝁𝒎𝒈𝒄𝒐𝒔𝜽 = 𝑚𝑎
𝑓
θ
𝑚𝑔𝑐𝑜𝑠𝜃
𝐹𝐴
𝐹𝑁
𝑊 = 𝑚𝑔
𝑓
21

22. 22

23. FBD for 𝑚1object
direction
Second law equation
𝐹𝑦 = 𝑇 − 𝑚1𝑔 = 𝑚1𝑎 … … . . 1
𝑇 − 𝑚1𝑔 = 𝑚1𝑎
FBD for 𝑚2object
𝐹𝑁
𝑚2𝑔
𝐹𝑐𝑜𝑠𝜃
𝐹𝑠𝑖𝑛𝜃
𝑓𝑘 = 𝜇𝑘𝐹𝑁
direction
Second law equation
𝐹𝑦 = 𝐹𝑁 + 𝐹𝑠𝑖𝑛𝜃 − 𝑚2𝑔 = 0 … … . . 2
𝐹
𝑥 = 𝐹𝑐𝑜𝑠𝜃 − 𝑇 − 𝑓𝑘 = 𝑚2𝑎 … … . . 4
(1)+(5): 𝑇 − 𝑚1𝑔 + 𝐹𝑐𝑜𝑠𝜃 − 𝑇 − 𝜇𝑘(𝑚2𝑔 − 𝐹𝑠𝑖𝑛𝜃) ==𝑚1𝑎+𝑚2𝑎
𝑎 =
𝐹 𝑐𝑜𝑠𝜃 − 𝜇𝑘𝑠𝑖𝑛𝜃 − (𝑚1+𝜇𝑘𝑚2)𝑔
(𝑚1+𝑚2)
−𝑚1𝑔 + 𝐹𝑐𝑜𝑠𝜃 − 𝜇𝑘(𝑚2𝑔 − 𝐹𝑠𝑖𝑛𝜃) = (𝑚1+𝑚2)𝑎
𝐹𝑐𝑜𝑠𝜃 − 𝑇 − 𝑓𝑘 = 𝑚2𝑎
𝐹𝑐𝑜𝑠𝜃 − 𝑇 − 𝜇𝑘(𝑚2𝑔 − 𝐹𝑠𝑖𝑛𝜃) = 𝑚2𝑎 … (5)
𝑭𝑵 = 𝒎𝟐𝒈 − 𝑭𝒔𝒊𝒏𝜽 … … … (3)
23

24. If the surface is rough, calculate the acceleration of the system
FBD 𝑚1
𝑇
𝑚1𝑔
Equation of motion
𝐹 = 𝑚1𝑎
𝑇 − 𝑚1𝑔 = 𝑚1𝑎 … (1)
FBD 𝑚2
𝑚𝑔𝑐𝑜𝑠𝜃
𝑇
𝒇
𝑚𝑔𝑠𝑖𝑛𝜃
𝐹𝑁
Equation of motion
𝐹 = 𝑚2𝑎
𝑚2𝑔𝑠𝑖𝑛𝜃 − 𝑇 − 𝑓 = 𝑚2𝑎 … (2)
1 + 2 : 𝑇 − 𝑚1𝑔 + 𝑚2𝑔𝑠𝑖𝑛𝜃 − 𝑇 − 𝑓 = 𝑚1𝑎 + 𝑚2𝑎
−𝑚1𝑔 + 𝑚2𝑔𝑠𝑖𝑛𝜃 − 𝑓 = (𝑚1+𝑚2)𝑎
(𝑚2𝑔𝑠𝑖𝑛𝜃 − 𝑚1𝑔 − (𝜇𝑚2𝑔𝑐𝑜𝑠𝜃) = (𝑚1+𝑚2)𝑎
(𝑚2𝑠𝑖𝑛𝜃 − 𝑚1 − 𝜇𝑚2𝑐𝑜𝑠𝜃)𝑔 = (𝑚1+𝑚2)𝑎
𝑎 =
(𝑚2𝑠𝑖𝑛𝜃 − 𝑚1 − 𝜇𝑚2𝑐𝑜𝑠𝜃)𝑔
(𝑚1+𝑚2)
𝑏𝑢𝑡 𝑓 = 𝜇𝐹𝑁 = 𝜇𝑚2𝑔𝑐𝑜𝑠𝜃
24

25. Using the following diagram, Show that 𝜇𝑠 = 𝑡𝑎𝑛𝜃
25

26. Equilibrium applications of Newton’s laws of
motion
An object is in equilibrium when it has zero net force and
zero acceleration along both x and y directions.
𝐹𝑥 = 0 … . (1) 𝐹𝑦 = 0 … … (2)
Problem solving strategy
Resolve all the forces into vertical and horizontal components
Force X component Y-component
𝐹1 𝐹1𝑥 𝐹1𝑦
𝐹2 𝐹2𝑥 𝐹2𝑦
𝐹3 𝐹3𝑥 𝐹3𝑦
𝐹𝑥 = 𝐹1𝑥 + 𝐹2𝑥 + 𝐹3𝑥 = 0….(1)
𝐹𝑦 = 𝐹1𝑦 + 𝐹2𝑦 + 𝐹3𝑦 = 0….(2)
26

27. Free body Diagrams
27

28. 𝑇1
𝑇2
𝑇3
−𝑇1𝑐𝑜𝑠𝜃1 𝑇1𝑠𝑖𝑛𝜃1
𝑇2𝑐𝑜𝑠𝜃2 𝑇2𝑠𝑖𝑛𝜃2
0 𝑇3 = 𝐹
𝑔
28

29. 𝑇1
𝑇2
𝑇3
−𝑇1𝑐𝑜𝑠𝜃1 𝑇1𝑠𝑖𝑛𝜃1
𝑇2𝑐𝑜𝑠𝜃2 𝑇2𝑠𝑖𝑛𝜃2
0 𝑇3 = −𝐹
𝑔
𝐹𝑥 = 0: −𝑇1𝑐𝑜𝑠𝜃1 + 𝑇2𝑐𝑜𝑠𝜃2 + 0 = 0 … … . . (1)
𝐹𝑦 = 0: 𝑇1𝑠𝑖𝑛𝜃1 + 𝑇2𝑠𝑖𝑛𝜃2 − 𝐹
𝑔 = 0 … … . . (2)
𝑇2 = 𝑇1
𝑐𝑜𝑠𝜃1
𝑐𝑜𝑠𝜃2
… … . . (3)
𝑇1𝑠𝑖𝑛𝜃1 + 𝑇1
𝑐𝑜𝑠𝜃1
𝑐𝑜𝑠𝜃2
𝑠𝑖𝑛𝜃2 − 𝐹
𝑔 = 0
𝑇1 =
𝐹
𝑔
𝑠𝑖𝑛𝜃1 + 𝑐𝑜𝑠𝜃1𝑡𝑎𝑛𝜃2
𝑇1 =
122
𝑠𝑖𝑛37° + 𝑐𝑜𝑠37°𝑡𝑎𝑛53°
= 73.4𝑁
𝑇2 = 73.4
𝑐𝑜𝑠37°
𝑐𝑜𝑠53°
= 97.4N … … . . (3)
29

30. Tutorial Questions
30

31. FBD
Horizontally: 𝐹𝑥 = 𝑚𝑎𝑥 :
𝐹𝑐𝑜𝑠𝜃 − 𝑓 = 𝑚𝑎𝑥
35.0𝑐𝑜𝑠𝜃 − 20.0 = (20.0)(0)
But 𝑎𝑥= 0 𝑚/𝑠2 since constant speed
𝜃 = 55. 20
𝐹𝑁 + 𝐹𝑠𝑖𝑛𝜃 = 𝑚𝑔
𝐹𝑁 = 𝑚𝑔 − 𝐹𝑠𝑖𝑛𝜃
𝐹𝑁 = 𝑚𝑔 − 𝐹𝑠𝑖𝑛𝜃
Vertically: 𝐹𝑦 = 0 𝑁
𝐹𝑁 = 167.0 𝑁
𝐹𝑁 = (20.0)(9.8) − 35.0 sin( 55. 20
)
31

32. 32

33. 1. Two forces act on a 4.5-kg block
resting on a frictionless surface as
shown. What is the magnitude of the
horizontal acceleration of the block?
The answer is A
A) 1.8 m/s2
B) 1.2 m/s2
C) 0.82 m/s2
D) 3.2 m/s2
E) 8.9 m/s2
33

34. 2. A 10-kg block is connected to a 40-kg
block as shown in the figure. The
surface on that the blocks slide is
frictionless. A force of 50 N pulls the
blocks to the right.
What is the magnitude of the acceleration of the 40-kg block?
A) 0.5 m/s2
B) 1 m/s2
C) 2 m/s2
D) 4 m/s2
E) 5 m/s2
The answer is B
34

35. 3. A 10-kg block is connected to a 40-kg
block as shown in the figure. The
surface on that the blocks slide is
frictionless. A force of 50 N pulls the
blocks to the right.
What is the magnitude of the tension T in the rope that connects the
two blocks ?
The answer is B
A) 0 N
B) 10 N
C) 20 N
D) 40 N
E) 50 N
35

36. 4. A block is at rest on a rough inclined plane and is connected to an
object with the same mass as shown. The rope may be considered
massless; and the pulley may be considered frictionless. The
coefficient of static friction between the block and the plane is µs; and
the coefficient of kinetic friction is µk.
What is the magnitude of the static frictional force acting on the block?
A) mg sin q
B) mg cos q
C) mg(1 – sin q)
D) mg(1 – cos q)
E) mg
The answer is C
36

37. 4. A block is at rest on a rough inclined plane and is connected to an
object with the same mass as shown. The rope may be considered
massless; and the pulley may be considered frictionless. The
coefficient of static friction between the block and the plane is µs; and
the coefficient of kinetic friction is µk.
If the rope were cut between the block and the pulley, what would be
the magnitude of the acceleration of the block down the plane?
The answer is E
A) g
B) g – k sin q
C) g – k cos q
D) g(tan q – k sin q)
E) g(sin q – k cos q)
37

38. 5. A block is at rest on a rough inclined plane and is connected to an
object with the same mass as shown. The rope may be considered
massless; and the pulley may be considered frictionless. The
coefficient of static friction between the block and the plane is µs; and
the coefficient of kinetic friction is µk.
If the mass of the suspended object is doubled, what will be the
acceleration of the block up the plane?
The answer is D
A) g(2 – k sin q)
B) 2g(k sin q – cos q)
C) g(2tan q – k sin q)
D) g(2 – sin q – k cos q)
E) g(2cos q – k sin q)
38

39. Additional Question
One 3.2-kg paint bucket is hanging by a
massless cord from another 3.2 kg paint bucket,
also hanging by a massless cord.
a. If the buckets are at rest, what is the tension
in each cord?
b. If the two buckets are pulled upward with an
acceleration of 1.60 m/s2 by the upper cord,
calculate the tension in each cord.
39

40. Test your understanding.
i
q
i
v
A fire fighter, a distance d from a burning building, directs a stream of
water from fire hose at angle above the horizontal as in the figure below.
, at what height does the water strike the building?
If the initial speed of the steam is
40