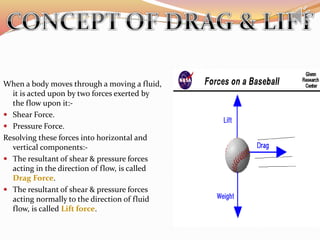
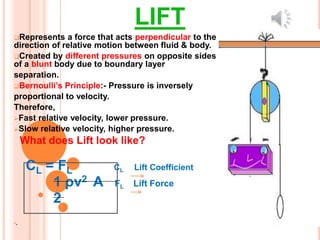
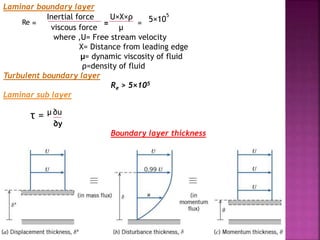
When a body moves through a fluid, it experiences two forces: drag and lift. Drag acts parallel to the flow and slows the body down, while lift acts perpendicular to the flow. These forces depend on factors like the fluid's velocity and density, the body's size and shape, and its angle of attack relative to the flow. Streamlined shapes with small frontal areas experience less pressure drag than blunt bodies, which experience boundary layer separation and higher pressures on one side. The forces can be calculated using drag and lift coefficients, which vary based on the Reynolds number and other flow properties.

1. DRAG FORCE & LIFT
PRESENTED BY
PRINCE SINGH

2. FLOW AROUND EXTERNAL
BODIES

3. You all must have come across soothing
breeze flow past around your face. It gives a
delightful pleasure to one’s heart. But have
you ever wondered about science behind it
????

5. When a body moves through a moving a fluid,
it is acted upon by two forces exerted by
the flow upon it:-
 Shear Force.
 Pressure Force.
Resolving these forces into horizontal and
vertical components:-
 The resultant of shear & pressure forces
acting in the direction of flow, is called
Drag Force.
 The resultant of shear & pressure forces
acting normally to the direction of fluid
flow, is called Lift force.

6. DRAG
 Drag is the retarding force exerted on a
moving body in a fluid medium
 It does not attempt to turn the object, simply
to slow it down
 It is a function of the speed of the body, the
size (and shape) of the body, and the fluid
through which it is moving.
What does drag look like?
Cd = Fd Cd Drag Coefficient
1ρv2 A Fd Drag force
2

7. LIFT
Represents a force that acts perpendicular to the
direction of relative motion between fluid & body.
Created by different pressures on opposite sides
of a blunt body due to boundary layer
separation.
Bernoulli’s Principle:- Pressure is inversely
proportional to velocity.
Therefore,
Fast relative velocity, lower pressure.
Slow relative velocity, higher pressure.
What does Lift look like?
CL = FL CL Lift Coefficient
1 ρv2 A FL Lift Force
2
•.

8. Cross-pollination Wind Mill
RBC Transportation in Body

9.  Parachuting is made
possible only due to Drag.
 Motion of sub-marine is
due to drag force acting on
body immersed in water
bodies.
 Generation of power using
turbine mills.
 Drag force acts as a tool to
test the active mechanical
response PC 12 neurites.

10. Streamlined Bodies- A
streamlined body is a shape that lowers
the friction between fluid like water and
air, and object moving through that fluid.
Blunt Bodies- A blunt body is the
one that as a result of its shape has
separated flow over a substantial part of
its surface.

11. 2-Dimensional fluid flow:- The flow over
a body is said to be 2 dimensional when the
body is very long & of constant cross-section
area & the flow is normal to the body.
Axis –Symmetric fluid flow:- The flow
in which the body possess rotational symmetry
about an axis in flow direction.
3-Dimensional fluid flow:-Flow over a
body that cannot be modeled as two-
dimensional or axis-symmetric, is called as 3-
dimensional fluid flow.

12.  Shear / Skin Friction Drag:- The part of the
drag that is due directly to wall shear
stress( τw ) is called skin friction drag.
CD,friction= FD,friction
1ρv2A
2
 Pressure / Form Drag:- The part of drag that
is directly due to pressure P, is called
the Pressure / Form Drag.
CD,Pressure= FD,Pressure
1ρv2A
2

13.  On orientation of body.
 Magnitude of wall shear
stress.
 Viscosity of fluid
 Reynolds number of flow
 Planform surface area
 Surface roughness under
turbulent conditions.

14.  Becomes significant
only when fluid velocity
is very high.
 Layer separation.
 Orientation of body.

15. The wings of air planes are streamlined
so as to minimize the drag force
experienced by it & maximize the lift
force that helps it in initial take off. The
wings are inclined at an angle of 5
(ranging between 5 to 15 ), called angle
of attack. In case of turbulent flows,
pressure drag dominates over shear
drag, which is reduced simply by
reducing the frontal surface area, which
in turn reduces boundary layer
separation, thus minimizing pressure
drag.

16. When a blunt body obstructs the path
of a fluid flow, the flow layer unable
to remain in contact in surface gets
separated, resulting in formation of
wake region. The fluid re-circulate in
low pressure wake region, the
phenomena known as Vortexing. The
point where the flow layer separates
is called separation point. The whole
phenomena results in formation of
high & low pressure regions at
opposite ends of body, thus
increasing the pressure drag acting
on body.

17. A flat plate 1.5m x 1.5m moves at
50km/h in stationary air of specific
weight 1.15kgf/m3 . If the coefficient of
drag and lift are 0.15 and 0.75
respectively, Determine :
• The lift force,
• The drag force,
• The resultant force.

18. Sol:
Area of plate(A) =1.5 x 1.5= 2.25m2
velocity of plate(U) =50km/h= 50 x
1000
3600
m/sec
specific weight of air, w= 1.15kgf/m3
Density of air , ρ =
𝑤
𝑔
=
1.15
9.81
=0.1172 kg/m3
coefficient of drag ,CD =0.15
Coefficient of lift, CL = 0.75
Using equation FL = CL Aρ
𝑈2
2
= 0.75 x 2.25 x0.1172 x
13.892
2
=19.078 kgf
Using equation, FD = CDAρ
𝑈2
2
=0.15 x 2.25 x0.1172 x
13.892
2
= 3.815 kgf
Resultant force, FR = FL
2
+ FD
2
= 19.0782 + 3.8152
= 363.47 + 14.554 kgf
=19.455 kgf

19. Boundary Layer Concept
magnetN S
Free stream velocity
Flow over a plate
Laminar boundary layer
Leading edge
Laminar sub layer
Turbulent boundary layer
Highly viscous region

20. Laminar boundary layer
Re =
Inertial force
=
U×X×ρ
= 5×10
5
viscous force μ
where ,U= Free stream velocity
X= Distance from leading edge
μ= dynamic viscosity of fluid
ρ=density of fluid
Turbulent boundary layer
Re > 5×105
Laminar sub layer
τ = μ ∂u
∂y
Boundary layer thickness

21. Distance BC=
Let y = distance of elemental strip from the plate
dy = thickness of elemental strip
u= velocity of fluid at elemental strip
D=width of plate
Area of strip dA =D × dy
Mass of fluid per second flowing through the element
strip
=ρ × velocity × area of
strip
= ρ × u× b× dy.
Consider no plate is present, so mass of fluid flowing through elemental strip=
ρ × velocity × area
= ρ×U×bdy
The reduction in mass per second flowing through elemental strip =ρUbdy-ρubdy
=ρb(U-u)dy
Total reduction in mass per second flowing through BC due to plate
=ρb 0∫ (U-u) dy
Let the plate is displaced by *, then the velocity of flow per the distance * is
equal to the free stream velocity
So, the loss of mass of fluid per second will be at *= ρ × velocity × area
= ρ×U× * × b

22. Equating equation 3 and 4 ,we get;
=ρb 0∫ (U-u) dy =ρU *b
* = 0 ∫ (1- u ) dy.
U

23. Momentum thickness
The distance by which a boundary layer should be displaced for the compensate for the
reduction in momentum of the flowing fluid on account of boundary layer formation.
The area of element strip = b dy
Mass of fluid on elemental area= ρ × velocity × area
= ρubdy
Momentum of fluid = mv
=ρubdy u
= ρu2bdy
If plate is not considered;
Momentum of fluid= ρuUbdy
Lass of momentum= ρb(uU-u2) dy
Total loss in momentum= ρbU 0∫ u(1-u ) dy
U

24. let θ = distance by which plate is displaced when the fluid is
flowing with constant velocity U ,
Therefore loss of momentum per second of fluid flowing
through distance θ with velocity U
=mass of fluid through θ × velocity
=ρ × velocity × area
=(ρθ×b ×U) ×U = ρθbU2
Equating eq.1 and 2;
θ= 0 ∫ u(1- u ) dy
U U

26. The shear stress is given by
=(μ
𝜕𝑢
𝜕𝑦
)y=0
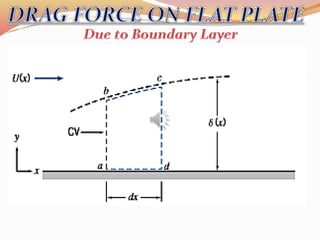
 Drag force or shear force on the small distance is given by
∆Fd= ∆xb
 Drag force ∆Fdmust be equal to the rate of change of momentum over
the distance ∆x
 The mass rate of flow entering through AD
= 0∫ (ρ× velocity × area of thickness dy)
= 0∫ ρubdy
 The mass rate of flow leaving side BC
mass through AD+
𝜕
𝜕𝑥
(mass through AD)× ∆𝑥
= 0
𝛿
𝜌𝑢𝑏𝑑𝑦 +
𝜕
𝜕𝑥
[ 0
𝛿
𝜌𝑢𝑏𝑑𝑦]∆𝑥
From continuity equation for a steady incompressible flow ,we have
MAD +MDC =MBC

27. MDC = MBC – MAD
=
𝜕
𝜕𝑥 0
𝛿
[𝜌𝑢𝑏𝑑𝑦]∆x
momentum flux entering through AD= 0
𝛿
[𝜌𝑢𝑏𝑑𝑦]x [u]
= 0
𝛿
𝜌u2bdy
Momentum flux entering through side BC = 0
𝛿
𝜌u2bdy =
𝜕
𝜕𝑥
[ 0
𝛿
𝜌u2bdy] ∆𝑥
So, momentum flux through DC =
𝜕
𝜕𝑥
[ 0
𝛿
𝜌ubdy] ∆𝑥 x U
Rate of change of momentum of control volume = MFBC - MFAD –MFDC
{ 0
𝛿
𝜌u2bdy +
𝜕
𝜕𝑥
[ 0
𝛿
𝜌u2bdy] ∆𝑥}-{ 0
𝛿
𝜌u2bdy}-{
𝜕
𝜕𝑥
[ 0
𝛿
𝜌ubdy] ∆𝑥 x u}
= 𝜌𝑏
𝜕
𝜕𝑥
[ 0
𝛿
(𝑢2 -𝑢𝑈)𝑑𝑦] × ∆𝑥

28. Total external force is in the direction of rate of change of
momentum;
-𝜏∆𝑥b =𝜌𝑏
𝜕
𝜕𝑥
[ 0
𝛿
(𝑢2 -𝑢𝑈)𝑑𝑦] × ∆𝑥
𝜏
𝜌𝑢2 = [
𝜕
𝜕𝑥 0
𝛿 𝑢
𝑈
(1-
𝑢
𝑈
) 𝑑𝑦]
𝜏
𝜌𝑢2 =
𝜕𝜃
𝜕𝑥
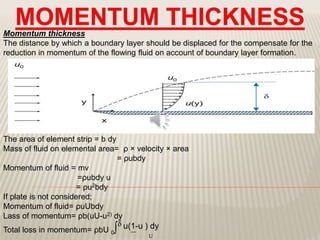
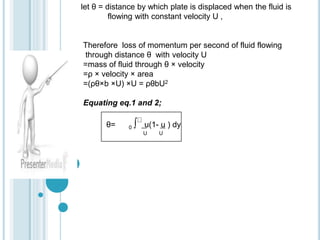
Where ; θ= Momentum thickness
This is Von karman momentum integral equation
This equation is applicable for all type of boundary layers.

29. Local coefficient of Drag [CD *]
CD * =
𝜏
𝑈2 𝜌
2
Average drag coefficient [CD ]
CD =
𝐹 𝐷
𝑈2 𝐴𝜌
2
Where; A = Area of plate
U= free stream velocity
ρ=mass density of fluid

30. Friction coefficient
The friction coefficient for laminar flow can be determined experimentally
by using conservation of mass and momentum together.
Average friction coefficient for entire plate can be determined as:
For laminar flow;
Boundary layer thickness(𝜹)= 4.91x for Cf,x = 0.664 Re< 5×105
Re
1/2
Re
1/2
The corresponding relation for turbulent flow are
𝜹 = 0.38x for Cf,x = 0.059 5×105 <Re<107
Re
1/5
Re
1/5
Cf = 1 ∫ Cf,x dx
L

31. In some cases a flat plate is sufficiently long enough to become turbulent
but it is not long enough to disregard the laminar flow regimes
So ,
Average friction coefficient for determining the friction coefficient for the region
= 0∫X
Cf,x laminardx + ∫L
Cf,x turbulent dx
Cf = 0.074 - 1742 5×105 <Re<107
Re
1/5
Re
For laminar flow, the friction coefficient depends on only the Reynolds
number ,and the surface roughness has no effect. further flow, however,
surface roughness causes the friction coefficient.

32. According to Navier stokes
equation, drag force on sphere:
FD = 3𝜋𝜇𝐷𝑈
,

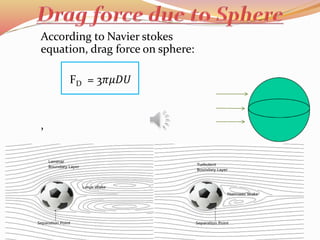
33. Expression for CD for Reynolds number less than 0.2
FD = CD A
𝜌𝑈2
2
FD =3𝜋𝜇𝐷𝑈
Equating both we get;
3𝜋𝜇𝐷𝑈 = CD A
𝜌𝑈2
2
Take A=
𝜋𝐷2
4
;
CD =
24
𝑅 𝑒
Expression for CD when 0.2< Re <5
CD =
24
𝑅 𝑒
[1+
3
16𝑅 𝑒
]
Note: 1:) for 5<Re <1000; CD =0.4
2:) For 103 <Re <105; CD = 0.5
3:)For Re >105 ; CD =0.2


34. Calculate the weight of ball of
diameter 8cm which is just
supported in a vertical airstream
which is flowing at a velocity of
7m/sec. The specific weight of air
is given as 1.25kg/m3 .The
kinematic viscosity of air =1.5
stokes.

35. Diameter of ball D = 8cm =0.08m
Velocity of air U = 7m/sec
Specific weight of air, w =1.25kgf/m3
so, density of air , ρ=
𝑤
𝑔
=
1.25
9.81
=0.1274 slug/m3
Kinematic viscosity 𝜗 =1.5stokes =1.5 x 10-4
m2/sec
Reynolds number, Re=
𝑈 𝑋 𝐷
𝜗
=
7 𝑋 0.08
1.5
x 104 =3730
Thus the value of Re lies between 1000 to 100000,
And hence CD =0.5
FD = CDAρ
𝑈2
2
=0.2 x 0.005026 x
.01274 ×7 ×7
2
= 0.007843 kgf