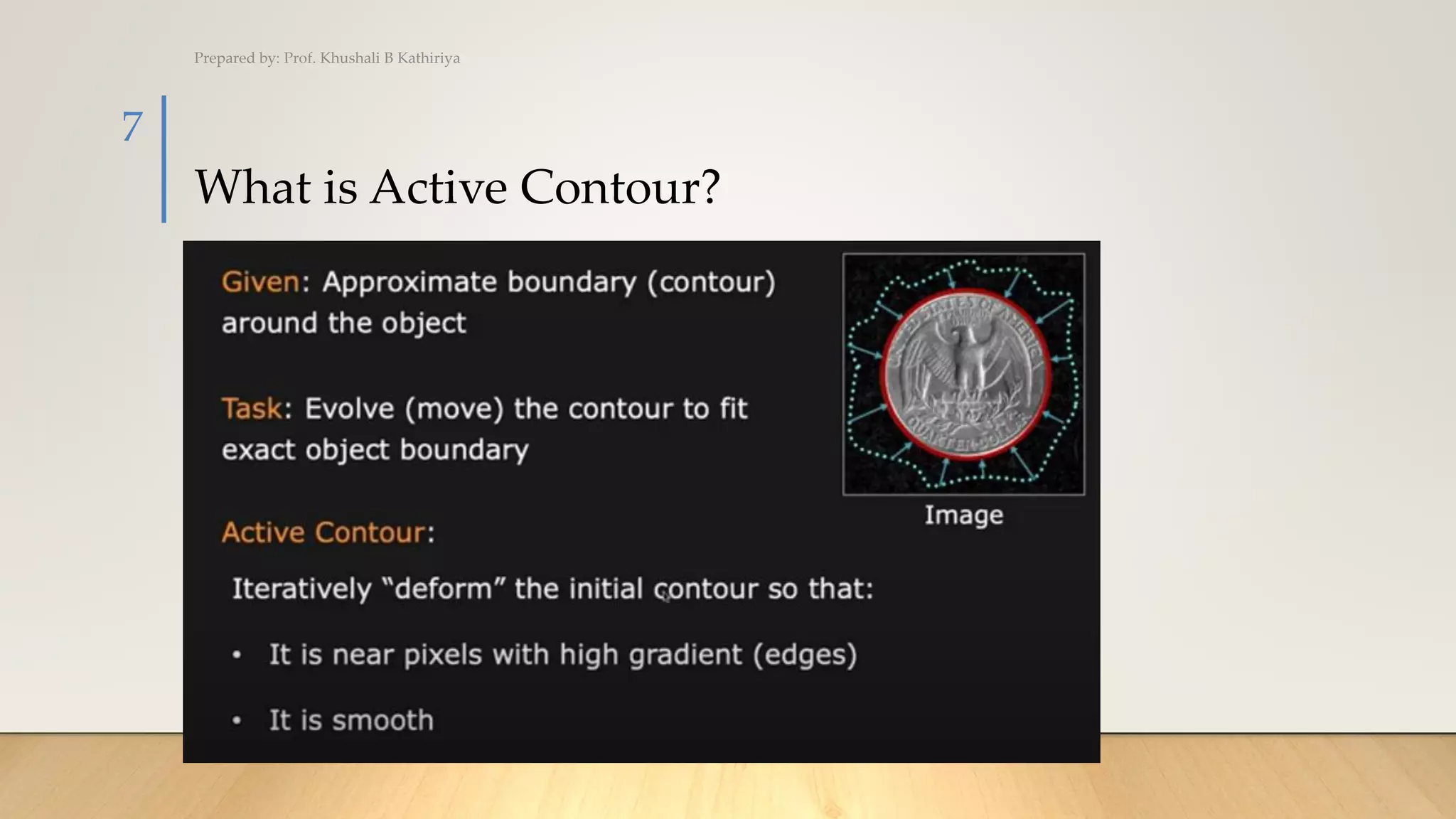
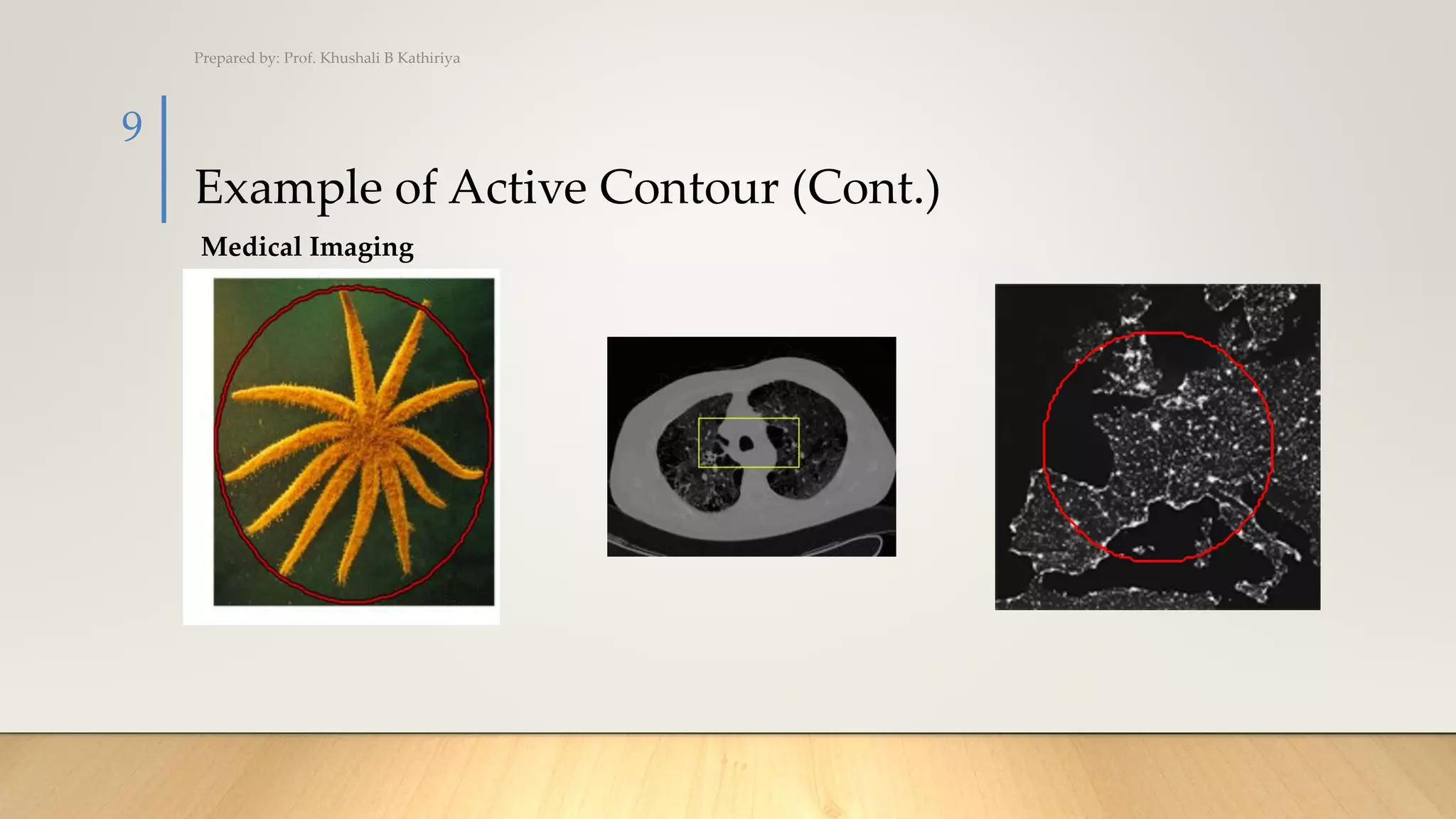
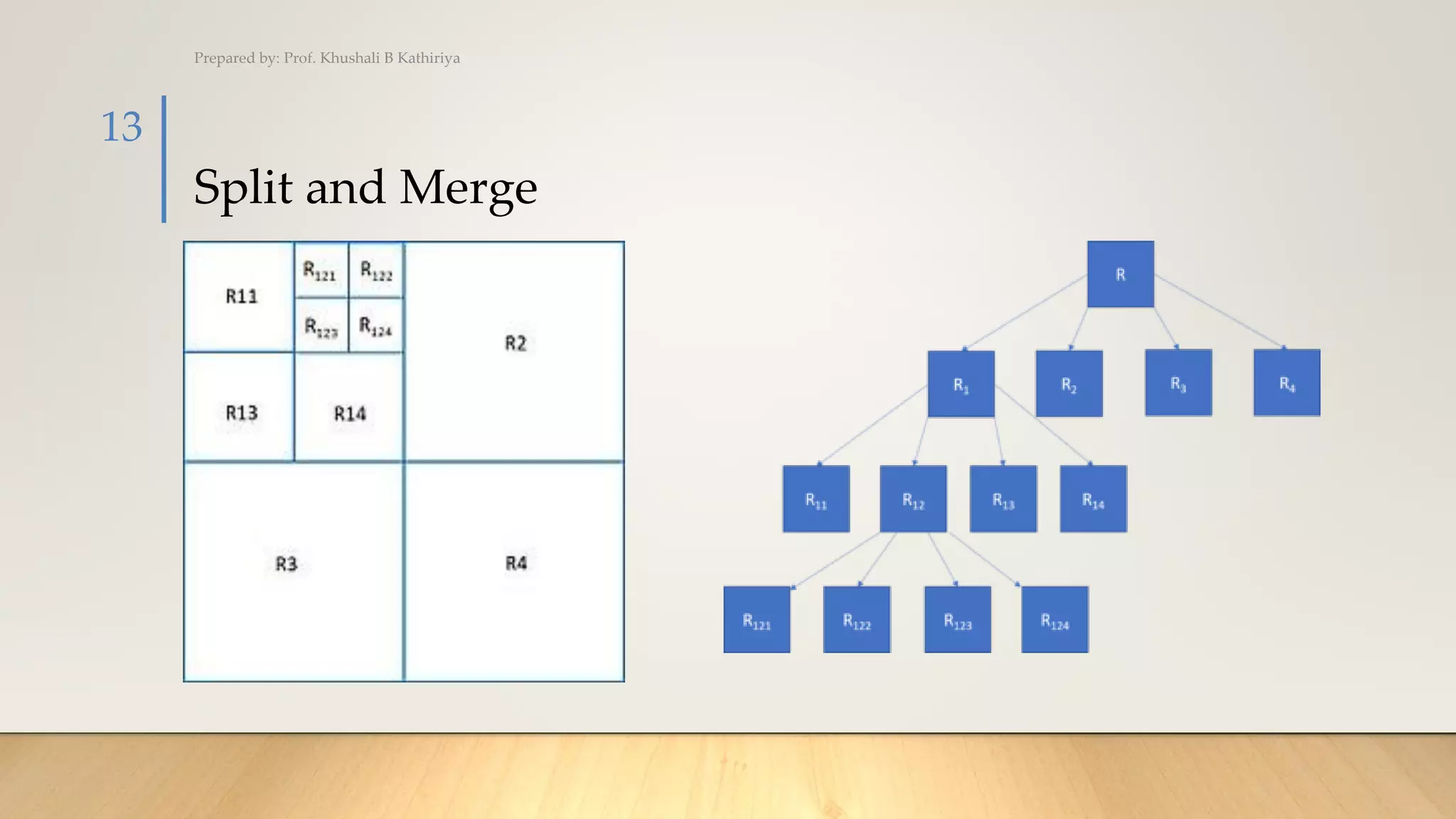
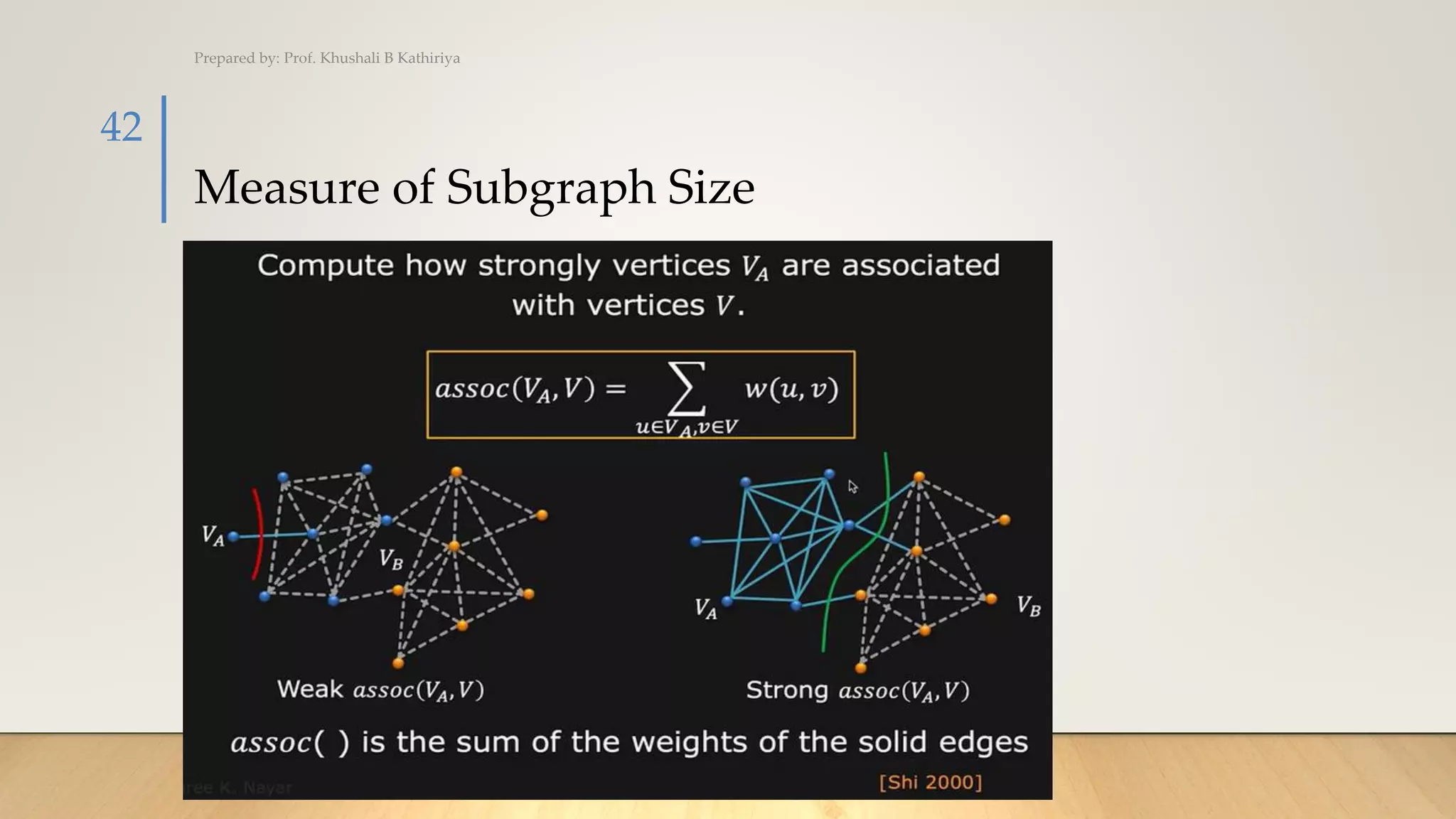
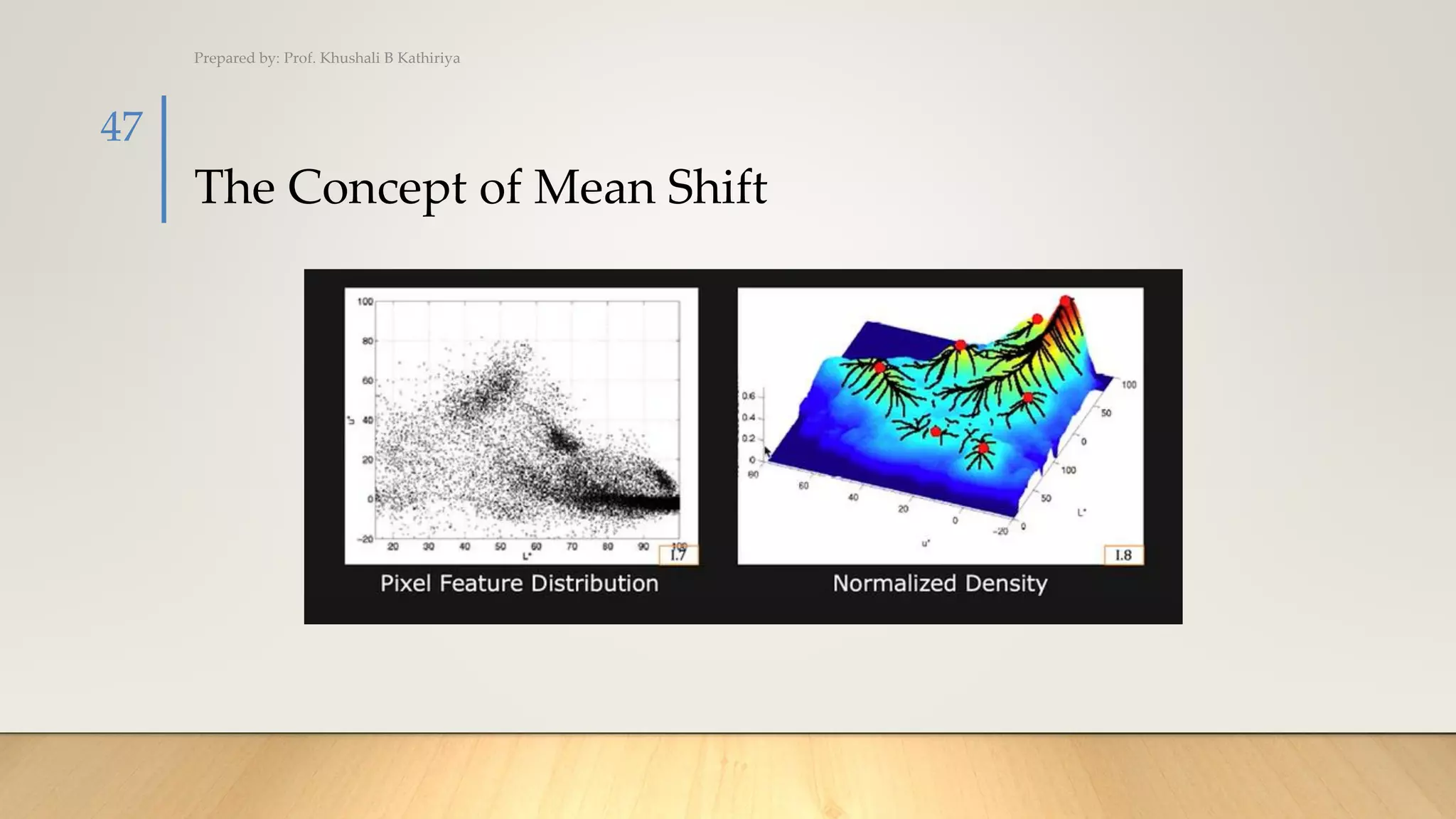
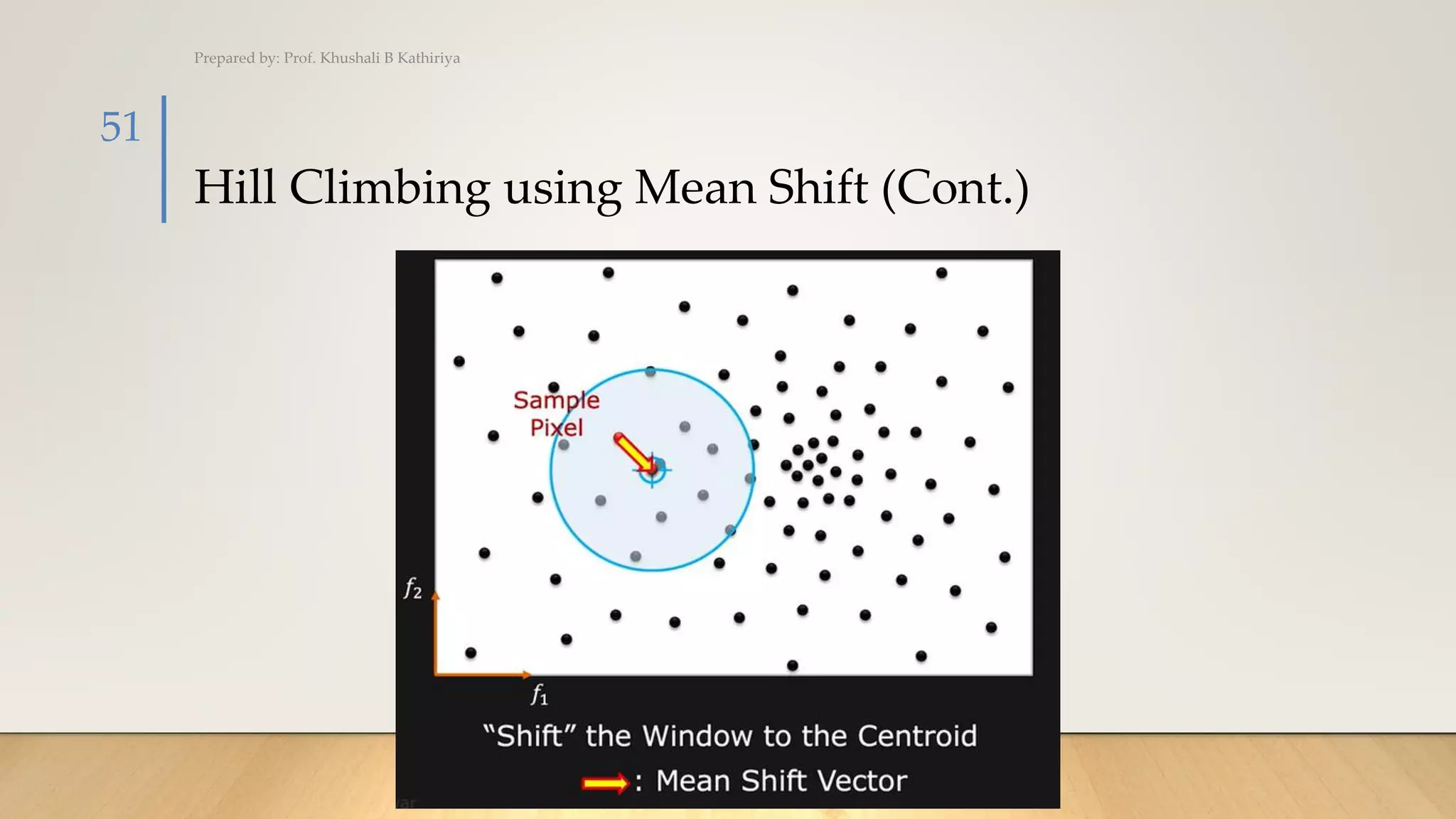
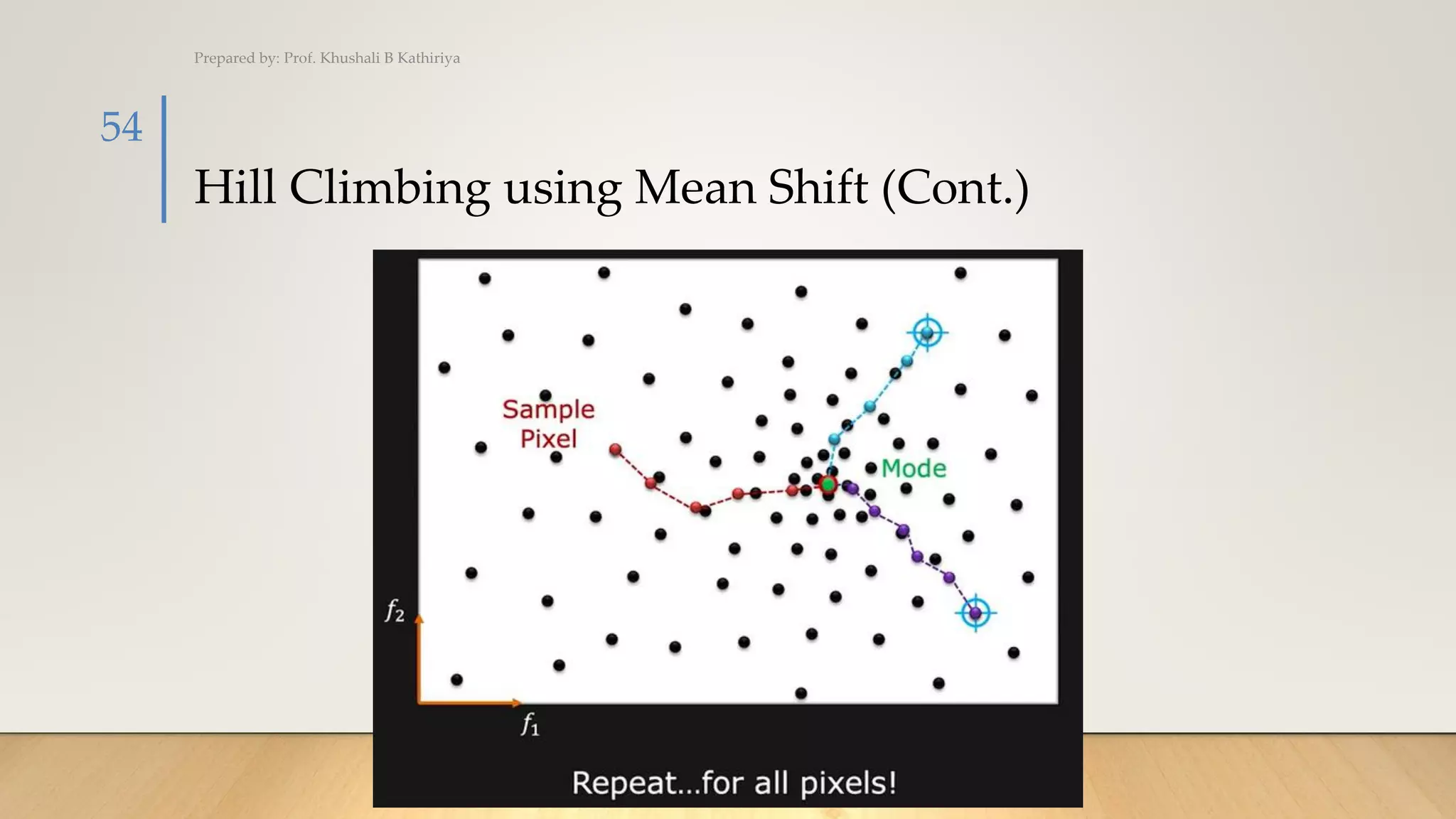
The document covers various techniques for image segmentation, including active contours, split and merge, watershed, graph-based segmentation, and mean shift. It explains how these methods facilitate the separation of target regions within images, featuring applications like medical imaging and motion tracking. Additionally, techniques such as the watershed algorithm are highlighted for effectively extracting overlapping objects.

1. Computer Vision
Chap.4 : Segmentation
SUB CODE: 3171614
SEMESTER: 7TH IT
PREPARED BY:
PROF. KHUSHALI B. KATHIRIYA

2. Outline
• Active Contours
• Split and Merge
• Watershed
• Region Splitting and Merging
• Graph-based Segmentation
• Mean shift and Model finding
• Normalized Cut
Prepared by: Prof. Khushali B Kathiriya
2

3. Active Contours
PREPARED BY:
PROF. KHUSHALI B. KATHIRIYA

4. Active Contour (Boundary Detection)
• Segmentation is a section of image processing for the separation or segregation
of information from the required target region of the image. There are different
techniques used for segmentation of pixels of interest from the image.
• Active contour is one of the active models in segmentation techniques, which
makes use of the energy constraints and forces in the image for separation of
region of interest. Active contour defines a separate boundary or curvature for
the regions of target object for segmentation.
Prepared by: Prof. Khushali B Kathiriya
4

5. Active Contour(Cont.)
• Application of Active Contour
• Medical Imaging
• Brain CT images
• MRI images
• Cardiac images
• Motion Tracking
• Stereo Tracking
Prepared by: Prof. Khushali B Kathiriya
5

6. What is Active Contour?
Prepared by: Prof. Khushali B Kathiriya
6

7. What is Active Contour?
Prepared by: Prof. Khushali B Kathiriya
7

8. Example of Active Contour
Prepared by: Prof. Khushali B Kathiriya
8

9. Example of Active Contour (Cont.)
Prepared by: Prof. Khushali B Kathiriya
9
Medical Imaging

10. Example of Active Contour (Cont.)
Prepared by: Prof. Khushali B Kathiriya
10
Motion Tracking

11. Split and Merge
PREPARED BY:
PROF. KHUSHALI B. KATHIRIYA

12. Split and Merge
• Split and merge segmentation is an image processing technique used
to segment an image. The image is successively split into quadrants based on
a homogeneity criterion and similar regions are merged to create the segmented
result. The technique incorporates a quadtree data structure, meaning that there
is a parent-child node relationship. The total region is a parent, and each of the
four splits is a child.
Prepared by: Prof. Khushali B Kathiriya
12

13. Split and Merge
Prepared by: Prof. Khushali B Kathiriya
13

14. Split and Merge Example
• The following example shows the segmentation of a gray scale image using
matlab. The homogeneity criterion is thresholding, max(region)-min(region) < 10
for a region to be homogeneous.
Prepared by: Prof. Khushali B Kathiriya
14

15. Split and Merge Example
• The blocks created during splitting are shown in the following picture:
Prepared by: Prof. Khushali B Kathiriya
15

16. Split and Merge Example
• And the segmented image is below.
Prepared by: Prof. Khushali B Kathiriya
16

17. Region Split and Merge
PREPARED BY:
PROF. KHUSHALI B. KATHIRIYA

18. Region Split and Merge Example (Cont.)
• Apply Region Split on following image. Assume that threshold value be <=3.
Prepared by: Prof. Khushali B Kathiriya
18
5 6 6 6 7 7 6 6
6 7 6 7 5 5 4 7
6 6 4 4 3 2 5 6
5 4 5 4 2 3 4 6
0 3 2 3 3 2 4 7
0 0 0 0 2 2 5 6
1 1 0 1 0 3 4 4
1 0 1 0 2 3 5 4

19. Region Split and Merge Example (Cont.)
• Step 1: Identify Max and Min pixel value from the whole image
• Max = 7
• Min = 0
• Max-Min= 7
• 7 <= 3 (Condition false)
• Split image
Prepared by: Prof. Khushali B Kathiriya
19
5 6 6 6 7 7 6 6
6 7 6 7 5 5 4 7
6 6 4 4 3 2 5 6
5 4 5 4 2 3 4 6
0 3 2 3 3 2 4 7
0 0 0 0 2 2 5 6
1 1 0 1 0 3 4 4
1 0 1 0 2 3 5 4

20. Region Split and Merge Example (Cont.)
• Step 1: Identify Max and Min pixel value from the whole image
• Max = 7
• Min = 0
• Max-Min= 7
• 7 <= 3 (Condition false)
• Split R image into R1a,R2b,cR3,R4d
Prepared by: Prof. Khushali B Kathiriya
20
5 6 6 6 7 7 6 6
6 7 6 7 5 5 4 7
6 6 4 4 3 2 5 6
5 4 5 4 2 3 4 6
0 3 2 3 3 2 4 7
0 0 0 0 2 2 5 6
1 1 0 1 0 3 4 4
1 0 1 0 2 3 5 4
R1a R2b
R3c R4d

21. Region Split and Merge Example (Cont.)
• Step 2: Compute for R1a region. Min and Max
• Max=7
• Min=4
• Max-Min=7-4=3
• 3 <= 3 (Condition true)
• No need to split R1a
Prepared by: Prof. Khushali B Kathiriya
21
5 6 6 6 7 7 6 6
6 7 6 7 5 5 4 7
6 6 4 4 3 2 5 6
5 4 5 4 2 3 4 6
0 3 2 3 3 2 4 7
0 0 0 0 2 2 5 6
1 1 0 1 0 3 4 4
1 0 1 0 2 3 5 4
R1a R2b
R3c R4d

22. Region Split and Merge Example (Cont.)
• Step 3: compute for R3c region. Min and Max
• Max=3
• Min=0
• Max-Min=3-0=3
• 3 <= 3 (Condition true)
• No need to split R3c
Prepared by: Prof. Khushali B Kathiriya
22
5 6 6 6 7 7 6 6
6 7 6 7 5 5 4 7
6 6 4 4 3 2 5 6
5 4 5 4 2 3 4 6
0 3 2 3 3 2 4 7
0 0 0 0 2 2 5 6
1 1 0 1 0 3 4 4
1 0 1 0 2 3 5 4
R1a R2b
R3c R4d

23. Region Split and Merge Example (Cont.)
• Step 4: Compute for R2b region. Min and Max
• Max=7
• Min=2
• Max-Min=7-2=5
Prepared by: Prof. Khushali B Kathiriya
23
5 6 6 6 7 7 6 6
6 7 6 7 5 5 4 7
6 6 4 4 3 2 5 6
5 4 5 4 2 3 4 6
0 3 2 3 3 2 4 7
0 0 0 0 2 2 5 6
1 1 0 1 0 3 4 4
1 0 1 0 2 3 5 4
R1a R2b
R3c R4d

24. Region Split and Merge Example (Cont.)
• Step 4: Compute for R2b region. Min and Max
• Max=7
• Min=2
• Max-Min=7-2=5
• 5 <= 3 (Condition false)
• Split R2b into R2b1,R2b2,R2b3,R2b4.
Prepared by: Prof. Khushali B Kathiriya
24
5 6 6 6 7 7 6 6
6 7 6 7 5 5 4 7
6 6 4 4 3 2 5 6
5 4 5 4 2 3 4 6
0 3 2 3 3 2 4 7
0 0 0 0 2 2 5 6
1 1 0 1 0 3 4 4
1 0 1 0 2 3 5 4
R1a R2b
R3c R4d

25. Region Split and Merge Example (Cont.)
• Step 5: Compute for R2b1,R2b2,R2b3,R2b4 region. Min and Max
• For all R2b1,R2b2,R2b3,R2b4
Condition have satisfied so no need
to splitting.
Prepared by: Prof. Khushali B Kathiriya
25
5 6 6 6 7 7 6 6
6 7 6 7 5 5 4 7
6 6 4 4 3 2 5 6
5 4 5 4 2 3 4 6
0 3 2 3 3 2 4 7
0 0 0 0 2 2 5 6
1 1 0 1 0 3 4 4
1 0 1 0 2 3 5 4
R1a R2b
R3c R4d

26. Region Split and Merge Example (Cont.)
• Step 6: Compute for R4d region. Min and Max
• Max=7
• Min=0
• Max-Min=7-0=7
Prepared by: Prof. Khushali B Kathiriya
26
5 6 6 6 7 7 6 6
6 7 6 7 5 5 4 7
6 6 4 4 3 2 5 6
5 4 5 4 2 3 4 6
0 3 2 3 3 2 4 7
0 0 0 0 2 2 5 6
1 1 0 1 0 3 4 4
1 0 1 0 2 3 5 4
R1a R2b
R3c R4d

27. Region Split and Merge Example (Cont.)
• Step 6: Compute for R4d region. Min and Max
• Max=7
• Min=0
• Max-Min=7-0=7
• 7 <= 3 (Condition false)
• Split R4d into R4d1,R4d2,R4d3,R4d4.
Prepared by: Prof. Khushali B Kathiriya
27
5 6 6 6 7 7 6 6
6 7 6 7 5 5 4 7
6 6 4 4 3 2 5 6
5 4 5 4 2 3 4 6
0 3 2 3 3 2 4 7
0 0 0 0 2 2 5 6
1 1 0 1 0 3 4 4
1 0 1 0 2 3 5 4
R1a R2b
R3c R4d

28. Region Split and Merge Example (Cont.)
• Step 7: Compute for R4d1,R4d2,R4d3,R4d4 region. Min and Max
• For all R4d1,R4d2,R4d3,R4d4
Condition have satisfied so no need
to splitting.
Prepared by: Prof. Khushali B Kathiriya
28
5 6 6 6 7 7 6 6
6 7 6 7 5 5 4 7
6 6 4 4 3 2 5 6
5 4 5 4 2 3 4 6
0 3 2 3 3 2 4 7
0 0 0 0 2 2 5 6
1 1 0 1 0 3 4 4
1 0 1 0 2 3 5 4
R1a R2b
R3c R4d

29. Watershed Segmentation
PREPARED BY:
PROF. KHUSHALI B. KATHIRIYA

30. Watershed Segmentation
• The watershed algorithm is a classic algorithm used for segmentation and is
especially useful when extracting touching or overlapping objects in images, such
as the coins in the figure above.
• Using traditional image processing methods such as thresholding and contour
detection, we would be unable to extract each individual coin from the image —
but by leveraging the watershed algorithm, we are able to detect and extract
each coin without a problem.
• When utilizing the watershed algorithm we must start with user-defined markers.
These markers can be either manually defined via point-and-click, or we
can automatically or heuristically define them using methods such as thresholding
and/or morphological operations.
Prepared by: Prof. Khushali B Kathiriya
30

31. Watershed Segmentation (Cont.)
Prepared by: Prof. Khushali B Kathiriya
31

32. Watershed Segmentation (Cont.)
Prepared by: Prof. Khushali B Kathiriya
32

33. The problem with basic thresholding and contour
extraction
Prepared by: Prof. Khushali B Kathiriya
33

34. Using the watershed algorithm for segmentation
Prepared by: Prof. Khushali B Kathiriya
34

35. Graph based Segmentation
PREPARED BY:
PROF. KHUSHALI B. KATHIRIYA

36. Graph based Segmentation
Prepared by: Prof. Khushali B Kathiriya
36

37. Measuring Affinity
Prepared by: Prof. Khushali B Kathiriya
37

38. Graph Cut Segmentation
Prepared by: Prof. Khushali B Kathiriya
38

39. Graph Cut Segmentation (Cont.)
Prepared by: Prof. Khushali B Kathiriya
39

40. Graph Cut Segmentation (Cont.)
Prepared by: Prof. Khushali B Kathiriya
40

41. Problem with Min-Cut
Prepared by: Prof. Khushali B Kathiriya
41

42. Measure of Subgraph Size
Prepared by: Prof. Khushali B Kathiriya
42

43. Normalized Cut (Ncut)
PREPARED BY:
PROF. KHUSHALI B. KATHIRIYA

44. Normalized Cut(Ncut)
Prepared by: Prof. Khushali B Kathiriya
44

45. Ncut Segmentation Results
Prepared by: Prof. Khushali B Kathiriya
45

46. The Concept of Mean Shift
PREPARED BY:
PROF. KHUSHALI B. KATHIRIYA

47. The Concept of Mean Shift
Prepared by: Prof. Khushali B Kathiriya
47

48. The Concept of Mean Shift (Cont.)
Prepared by: Prof. Khushali B Kathiriya
48

49. Hill Climbing using Mean Shift
Prepared by: Prof. Khushali B Kathiriya
49

50. Hill Climbing using Mean Shift (Cont.)
Prepared by: Prof. Khushali B Kathiriya
50

51. Hill Climbing using Mean Shift (Cont.)
Prepared by: Prof. Khushali B Kathiriya
51

52. Hill Climbing using Mean Shift (Cont.)
Prepared by: Prof. Khushali B Kathiriya
52

53. Hill Climbing using Mean Shift (Cont.)
Prepared by: Prof. Khushali B Kathiriya
53

54. Hill Climbing using Mean Shift (Cont.)
Prepared by: Prof. Khushali B Kathiriya
54

55. Mean Shift Algorithm
Prepared by: Prof. Khushali B Kathiriya
55

56. K-mean Vs. Mean shift
Prepared by: Prof. Khushali B Kathiriya
56

57. Example of K-mean Vs. Mean shift
Prepared by: Prof. Khushali B Kathiriya
57

58. Result of Mean Shift Segmentation
Prepared by: Prof. Khushali B Kathiriya
58