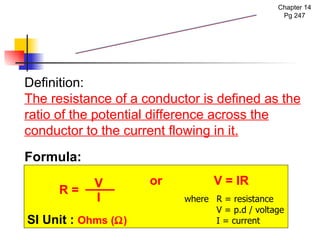
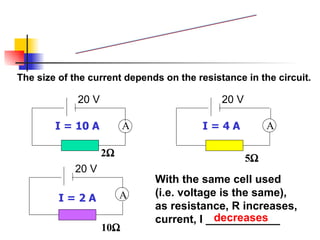
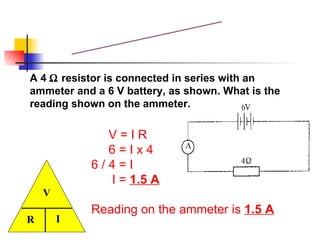
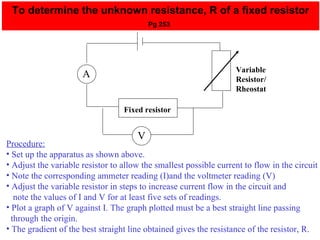
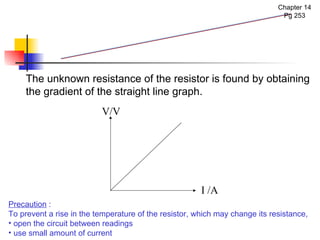
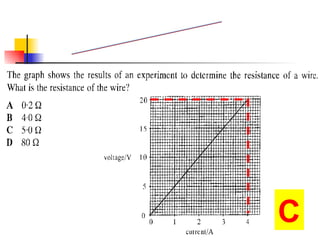
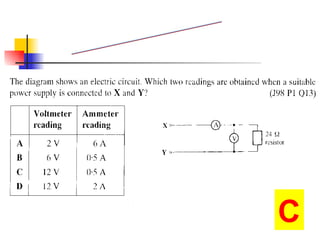
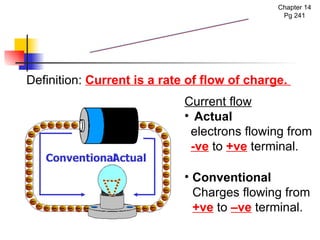
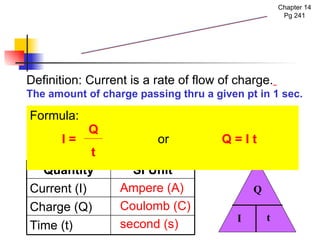
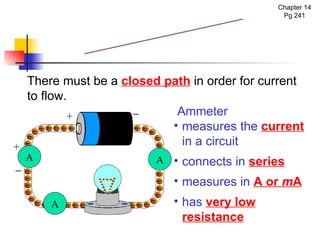
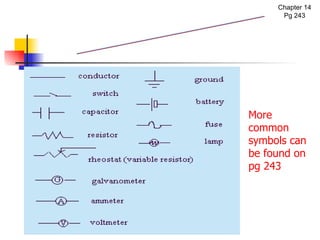
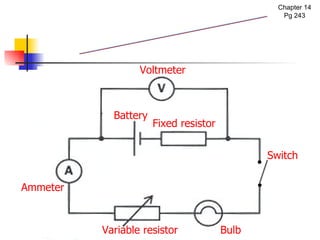
The document covers the fundamentals of electric current, including the definitions of current, electromotive force (e.m.f.), potential difference (p.d.), and resistance, along with their respective formulas and units. It provides examples demonstrating how to calculate current, charge, and resistance using various scenarios. Additionally, it explains measurement instruments like ammeters and voltmeters and their functions in electric circuits.

1. Electric current Electromotive force & Potential Difference Resistance Chapter 16: Current Electricity Part I

2. state that current is a rate of flow of charge and that it is measured in amperes recall the relationship charge = current x time apply the relationship to new situations or to solve related problems Chapter 14 At the end of the chapter, you should be able to: 1. Electric Current

3. Electric Current Current flow Actual electrons flowing from -ve to +ve terminal. Chapter 14 Pg 241 Definition: Current is a rate of flow of charge. Conventional Charges flowing from +ve to –ve terminal. Actual Conventional

4. Ampere (A) Coulomb (C) second (s) Measurement of Current Definition: Current is a rate of flow of charge. The amount of charge passing thru a given pt in 1 sec. Chapter 14 Pg 241 Time (t) Charge (Q) Current (I) SI Unit Quantity Q _______ I t Formula: I = or Q = I t Q t

5. Example 1: A current of 10 A flows through an electric heater for 10 minutes. What is the total charge circulated through the heater? [Solution] t = 10 min x 60 = 600 s I = 10 A Q = I t = 10 A x 600 s = 6000 C The total charge is 6000 C Measurement of Current Chapter 14 Q _______ I t

6. Example 2: In an electrical circuit, a charge of 60C flows past a point in 10s. What is the current in the circuit? Measurement of Current Chapter 14 [Solution] t = 10 s ; Q = 60 C Q = I t I = = 60 / 10 = 6 A The current is 6 A Q _______ I t Q t

7. Example 3: A lightning flash carries 25 C of charge and lasts for 0.01 s. What is the current? [Solution] Q = 25 C ; t = 0.01 s Q = I t 25 C = I x 0.01s 25 / 0.01 = I I = 2500A Current is 2500A Measurement of Current Chapter 14

8. Example 4: A current of 2 A is flowing through a conductor. How long does it take for 10 C of charge to pass any point? [Solution] I = 2 A ; Q = 10 C Q = I t 10C = 2A x t 10 / 2 = t t = 5 s Time taken is 5 s Measurement of Current Chapter 14

9. Ammeter measures the current in a circuit connects in series measures in A or m A has very low resistance There must be a closed path in order for current to flow. Ammeter Chapter 14 Pg 241 A A A +  + 

10. More common symbols can be found on pg 243 Chapter 14 Pg 243 Electric Symbols

11. Circuit Diagram Variable resistor Bulb Ammeter Voltmeter Battery Fixed resistor Switch Chapter 14 Pg 243

12. Electric current Electromotive force & Potential Difference Resistance Chapter 14: Current Electricity Chapter 14 Pg 245 Part II

13. define electromotive force (e.m.f.) as the work done by a source in driving a unit charge around a complete circuit state that the potential difference (p.d.) across a circuit component is measured in volts At the end of the chapter, you should be able to: 2. Electromotive Force & Potential Difference Chapter 14 Pg 245

14. Electromotive Force (e.m.f) Chapter 14 Pg 245 Definition: Electromotive force is defined as the total work done by a source in driving a unit charge around a complete circuit 1 Unit charge = 1 coulomb of charge

15. Electromotive Force (e.m.f) Chapter 14 Pg 245 Sources of e.m.f are: Electrical cells (i.e. batteries) Thermocouples Generators etc

16. 2V Electromotive Force (e.m.f) Hi I’m Mr Coulomb (1 C) 2J of energy 2J of energy 2 J of work is done when 1 C of charge moves round the circuit Mr Coulomb goes back to the source for energy Note: 2J of electrical energy 2J of light and heat energy 2 J of energy is supplied by the cell in moving 1 C of charge round

17. Electromotive Force (e.m.f) Chapter 14 Pg 245 Cell Source of energy Produces e.m.f that pushes the charges round the circuit. Work done/energy is used to light up the bulb. Direction of current travel

18. Analogy The pump pushes the water to flow flow of water Work done/ energy is used to move the mill

19. Potential Difference (p.d.) Chapter 14 Pg 246 Definition: The p.d. between two points is the energy required to move 1 C of charge between them. Potential Difference (p.d.) OR Voltage (V) SI Unit : V (volts)

20. The p.d. between 2 points is the energy required to move 1 C of charge between the two points. energy E p.d. = --------------- , V = ------ or E = VQ charge Q e.g. 2V = 2 J/C Potential Difference (p.d.) Formula: E _______ V Q

21. V Voltmeter measures the p.d. / voltage between 2 points connects in parallel across 2 points measures in V or mV has very high resistance +  +  Voltmeter Chapter 14 Pg 247 2J of energy 2J of energy

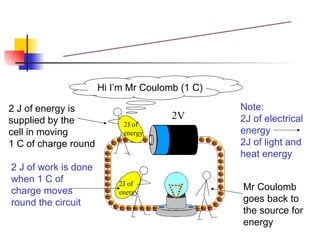
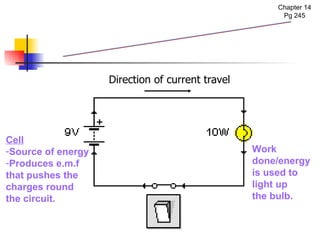
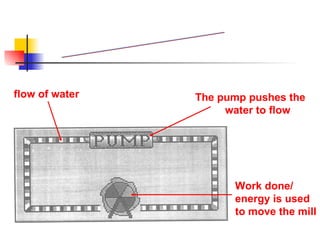
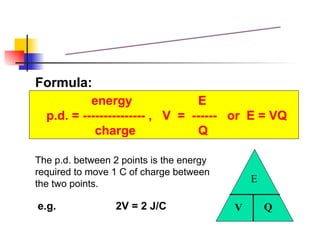
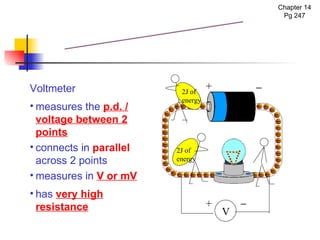
22. The diagram shows a battery with an electromotive force of 6 V in a circuit. How much energy is needed to drive 30C of charge round the circuit? E = VQ = 6V x 30C = 180 J or [Solution] Example 1 6 V

23. An electrical quantity is defined by “the energy converted by a source in driving unit charge round a complete circuit”. What is this quantity called? Current B. Electromotive force C. Potential difference D. Power Example 2 B

24. When a current of 0.5 A flows for 10 minutes through an electrical heater, 2400 J of energy is transformed. Calculate the total charge moving through the heater. (b) Calculate the potential difference across the heater. Q = I t = 0.5A x (10 x 60)s = 300 C Total charge is 300 C E = V Q 2400J = V x 300C V = 2400 / 300 = 8 V The p.d. is 8 V Example 3

25. Electric current Electromotive force & Potential Difference Resistance Chapter 14: Current Electricity Chapter 14 Pg 247 Part III

26. Chapter 14 Pg 247 The resistance is a measure of how difficult it is for an electric current to pass through a substance. Resistance

27. Chapter 14 Pg 247 Definition: The resistance of a conductor is defined as the ratio of the potential difference across the conductor to the current flowing in it. Resistance Formula: R = SI Unit : Ohms (  ) V I where R = resistance V = p.d / voltage I = current or V = IR

28. The size of the current depends on the resistance in the circuit. A A 2  5  10  With the same cell used (i.e. voltage is the same), as resistance, R increases, current, I ____________ Resistance 20 V 20 V 20 V decreases I = 10 A I = 4 A I = 2 A A

29. Resistance resists the flow of current Resistance is low in conductors and very high in insulators . Flow of current Resistance Resistance Chapter 14 Pg 248

30. V = I R 6 = I x 4 6 / 4 = I I = 1.5 A Reading on the ammeter is 1.5 A A 4  resistor is connected in series with an ammeter and a 6 V battery, as shown. What is the reading shown on the ammeter. Example 1 R I _______ V

31. Chapter 14 Pg 249 The resistance R (= V / I) of a metallic conductor is CONSTANT under steady physical conditions Ohm's Law

32. For Ohmic conductors (Conductors that obeys Ohm’s law) e.g. pure metal Chapter 14 Pg 248 For non-Ohmic conductor e.g. filament lamp bulb I /A V/V I /A V/V Metal A Metal B I /A V/V

33. an electrical component designed to reduce the flow of current. converts electrical energy to heat energy. (e.g. resistors used in electric fire and filament bulb convert electrical to heat and light energy) represented by the symbol Resistor

34. Rheostat a variable resistor that controls the size of a current in a circuit represented by Resistor

35. Procedure: Set up the apparatus as shown above. Adjust the variable resistor to allow the smallest possible current to flow in the circuit Note the corresponding ammeter reading (I)and the voltmeter reading (V) Adjust the variable resistor in steps to increase current flow in the circuit and note the values of I and V for at least five sets of readings. Plot a graph of V against I. The graph plotted must be a best straight line passing through the origin. The gradient of the best straight line obtained gives the resistance of the resistor, R. To determine the unknown resistance, R of a fixed resistor Pg 253 Fixed resistor A V Variable Resistor/ Rheostat

36. The unknown resistance of the resistor is found by obtaining the gradient of the straight line graph. Precaution : To prevent a rise in the temperature of the resistor, which may change its resistance, open the circuit between readings use small amount of current Experiment to find Resistance Chapter 14 Pg 253 I /A V/V

37. Example 2 C

38. Example 3 C

39. Example 4 B

40. Example 5 B

41. Resistivity Besides physical conditions (e.g. temperature), the resistance R of a given conductor also depends on: its length l its cross-sectional area A the type of material

42. Resistivity Formula: where R = resistance ρ = resistivity l = length A = cross-sectional area

43. Example 6

44. Example 7

45. Resistors in Series Resistors in Parallel Simulation from Crocodile Physics

46. Example 8

47. Example 9