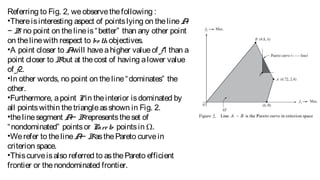
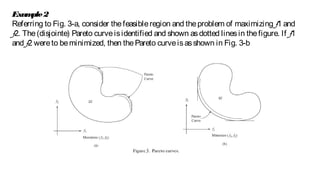
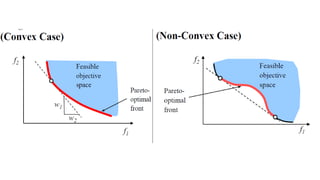
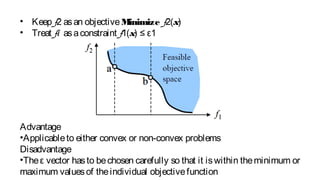
This document discusses multiobjective optimization problems which involve simultaneously maximizing or minimizing multiple criteria. It provides three key points: 1) Multiobjective optimization problems seek to find Pareto optimal solutions, where improving one objective cannot be achieved without worsening another. The set of Pareto optimal solutions is known as the Pareto frontier. 2) Several methods can solve multiobjective problems, including the weighted sum, ε-constraint, and lexicographic methods. These generate a set of Pareto optimal solutions. 3) The weighted sum method scalarizes objectives into a single objective using weights. The ε-constraint method optimizes one objective subject to constraints on the others. The lexicographic method sequentially optimizes objectives

1. Multiobjective Optimization
Prepared By
Mohammed Amer Kamil

2. Theengineer isoften confronted with “simultaneously” minimizing (or
maximizing) different criteria. Thestructural engineer would liketo
minimizeweight and also maximizestiffness; in manufacturing, one
would liketo maximizeproduction output and quality while
minimizing cost and production time.
Thesepractical applicationsarewerefer to them asmultiobjective
optimization problems.
Introduction

3. Mathematically, theproblem with multipleobjectivesmay bestated as
wheretheweightswi are≥ 0, ∑wi = 1. Theweightsarechosen from
experience.

4. Example:
Eachunit of product Y requires2 hoursof machining in thefirst cell and 1 hour in the
second cell. Each unit of product Z requires3 hoursof machining in thefirst cell and 4
hoursin thesecond cell. Availablemachining hoursin each cell = 12 hours. Each unit
of Y yieldsaprofit of $0.80, and each unit of Z yields$2. It isdesired to
determinethenumber of unitsof Y and Z to bemanufactured to maximize:
(i) total profit
(ii) consumer satisfaction, by producing asmany unitsof thesuperior quality product
Y. If x1 and x2 denotethenumber of unitsof Yand Z, respectively, then theproblem is:
maximizef1 = 0.8 x1 + 2 x2 and f2 = x1
subject to
2x1 + 3 x2 ≤ 12
x1 + 4 x2 ≤ 12
x1, x2 ≥ 0
Concept of Pareto Optimality

5. Thepreceding problem isshown graphically in Fig.1. Point Aisthesolution if
only f1 isto bemaximized, whilepoint Bisthesolution if only f2 isto be
maximized. For every point in x1 − x2 space, thereisapoint ( f ((x1), f (x2)) in
criterio n space.

6. Referring to Fig. 2, weobservethefollowing :
•Thereisinteresting aspect of pointslying on theline A
− B: no point on thelineis“better” than any other point
on thelinewith respect to bo th objectives.
•A point closer to Awill haveahigher valueof f1 than a
point closer to Bbut at thecost of having alower value
of f2.
•In other words, no point on theline“dominates” the
other.
•Furthermore, apoint Pin theinterior isdominated by
all pointswithin thetriangleasshown in Fig. 2.
•thelinesegment A− Brepresentstheset of
“nondominated” pointsor Pareto pointsin Ω.
•Werefer to thelineA− BasthePareto curvein
criterion space.
•Thiscurveisalso referred to asthePareto efficient
frontier or thenondominated frontier.

7. • general, no solution vector X existsthat maximizeall theobjectivefunctions
simultaneously..
• A feasiblesolution X iscalled Pareto optimal if thereexistsno other feasible
solution Y such that
fj(Y) ≤ fi(X) for i = 1, 2, . . . , k
with fj(Y) < fi(X) for at least onej.
• In other words, afeasiblevector X iscalled Pareto optimal if thereisno other
feasiblesolution Y that would maximizesomeobjectivefunction without causing a
simultaneousdecreasein at least oneother objectivefunction.
Definition of Pareto Optimality

8. Example2
Referring to Fig. 3-a, consider thefeasibleregion and theproblem of maximizing f1 and
f2. The(disjointe) Pareto curveisidentified and shown asdotted linesin thefigure. If f1
and f2 wereto beminimized, then thePareto curveisasshown in Fig. 3-b

9. • Several methodshavebeen developed for solving amultiobjective
optimization problem.
• Someof thesemethodswill bebriefly described in thefollowing slides.
• Most of thesemethodsbasically generateaset of Pareto optimal solutions
and usesomeadditional criterion or ruleto select oneparticular Pareto
optimal solution asthesolution of themultiobjectiveoptimization
problem.
Solving a multiobjective optimization
problem

10. Weighted Sum Method
• Weight of an objectiveischosen in proportion to therelativeimportance
of theobjective.
• Scalarizeaset of objectivesinto asingleobjectiveby adding each
objectivepre-multiplied by auser supplied weight .

11. Advantage
•Simple
Disadvantage
•It isdifficult to set theweight vectorsto obtain aPareto-optimal
solution in adesired region in theobjectivespace
•It cannot find certain Pareto-optimal solutionsin thecaseof a
nonconvex objectivespace

13. • Keep just oneof theobjectiveand restricting therest of the
objectiveswithin user-specific values.
-ε Constraint Method

14. • Keep f2 asan objectiveMinimize f2(x)
• Treat f1 asaconstraint f1(x) ≤ ε1
Advantage
•Applicableto either convex or non-convex problems
Disadvantage
•Theε vector hasto bechosen carefully so that it iswithin theminimum or
maximum valuesof theindividual objectivefunction

15. Lexicographic Method
With thelexicographic method, preferencesareimposed by ordering the
objectivesaccording to their importanceor significance, rather than by
assigning weights. Theobjectivefunctionsarearranged in theorder of
their importance. Then, thefollowing optimization problemsaresolved
oneat atime:
• Here, i representsafunction’sposition in thepreferred sequence, and
fj(x*j ) representstheminimum valuefor thejth objectivefunction,
found in thejth optimization problem.

16. Advantages:
•it isauniqueapproach to specifying preferences.
•it doesnot requirethat theobjectivefunctionsbenormalized.
•it alwaysprovidesaPareto optimal solution.
Disadvantages:
•it can requirethesolution of many singleobjectiveproblemsto obtain just
onesolution point.
•it needsadditional constraintsto beimposed.