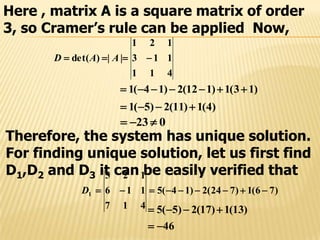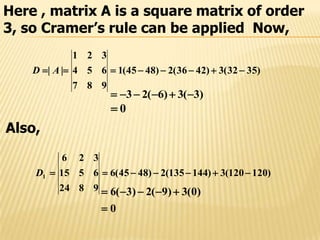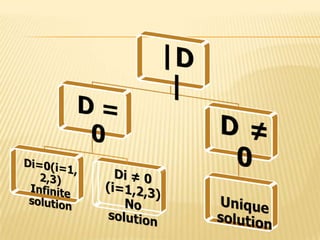
1) Cramer's rule can be used to solve systems of linear equations. It expresses the solution in terms of the determinants of the coefficient matrix and matrices with one column replaced by the constants vector. 2) If the determinant of the coefficient matrix is non-zero, there is a unique solution. If it is zero, there may be no solution or infinitely many solutions. 3) Three examples demonstrate applying Cramer's rule to find the unique solution, that there is no solution, and that there are infinitely many solutions, respectively.

1. Vector Calculus And
Linear Algebra
Presented by :
Abdul Sattar

2. CRAMER'S RULE
(Using Determinants to solve systems of equations)

3. INTRODUCTION
 Suppose that we have a square system
with n equation in the same number of
variables ( ). Then the
solution of the system has the
following cases.
1) If the system has non-zero
coefficient determinant D=det(A),
then the system has unique solution
and this solution is of the form
nxxx ,......., 21
,,.......,,
D
D
x
D
D
x
D
D
x n
n  2
2
1
1
iD
th
i nbbb ,.....,, 21

4. a) if at least one of Di is non-zero then
the system has no solution
b) if all Di‘s are zero, then the system
has infinite number of solutions.
In this case,
if the given system is homogeneous;
that is, right hand side is zero
then we have ffollowing possibilities of
its solution.
2) If the system has zero coefficient
determinant D=det(A) , then we have
two possibilities as discussed below.

6. EXAMPLE : 1
Find the solution of the system
Solution :
In matrix form, the given system of
equations can be written as Ax=b,
where
74
63
52



zyx
zyx
zyx

































7
6
5
,,
411
113
121
b
z
y
x
xA

7. Here , matrix A is a square matrix of order
3, so Cramer’s rule can be applied Now,
411
113
121
||)det(  AAD
)4(1)11(2)5(1 
023 
)13(1)112(2)14(1 
Therefore, the system has unique solution.
For finding unique solution, let us first find
D1,D2 and D3 it can be easily verified that
)76(1)724(2)14(5
417
116
125
1 D
46
)13(1)17(2)5(5



8. EXAMPLE : 2
Find the solution of the system
7242
532
32



zyx
zyx
zyx
Solution :
In matrix form, the given system of
equations can be written as Ax=b,
where

































7
5
3
,,
242
312
121
b
z
y
x
xA

9. )621(1)112(5)724(1
471
163
151
2 D
23
)15()11(517


)13(5)621(2)67(1
711
613
521
3 D
23
)4(5)15(213


Therefore, the system has unique solution.
1
23
23
,1
23
23
,2
23
46 321










D
D
z
D
D
y
D
D
x

10. Here , matrix A is a square matrix of order
3, so Cramer’s rule can be applied Now,
)28(1)64(2)122(1
242
312
121
||  AD
6)2(210 
0
Therefore, either the system has no
solution or infinite number of solution. Let
us check for it.
)720(1)2110(2)122(3
247
315
123
1 D
13)11(2)10(3 
05 
Therefore, the system has no solution as at
least one Di, i=1,2,3 is nonzero.

11. EXAMPLE : 3
Find the solution of the system
24987
15654
632



zyx
zyx
zyx
Solution :
In matrix form, the given system of
equations can be written as Ax=b,
where

































24
15
6
,,
987
654
321
b
z
y
x
xA

12. Here , matrix A is a square matrix of order
3, so Cramer’s rule can be applied Now,
)3532(3)4236(2)4845(1
987
654
321
||  AD
)3(3)6(23 
0
Also,
)120120(3)144135(2)4845(6
9824
6515
326
1 D
0
)0(3)9(2)3(6



13. )10596(3)4236(6)144135(1
9247
6154
361
2 D
0
)9(3)6(69


)3532(6)10596(2)120120(1
2487
1554
621
3 D
0
)3(6)9(20


Therefore, the system has infinitle number
of solutions.
Now, 0385
54
21


14. Therefore, þ(A)=2
Omitting m-r = 3-2 = 1
Considering n-r = 3-2 = 1 variable as
arbitary, the remaining system becomes
xzy
xzy
41565
632


Where x is arbitary
Now ,
31512
65
32
D
96)415(3)636(
6415
36
1 


 xxx
x
x
D
xxx
x
x
D 3)6(5)415(2
4155
62
1 




15. Therefore ,
x
x
D
D
zx
x
D
D
y 






3
3
,23
3
96 21
Let x = k , where k is arbitary , then the
infinite number of solutions of the given
system is kzkykx  ,23,
where k is an arbitary constant.