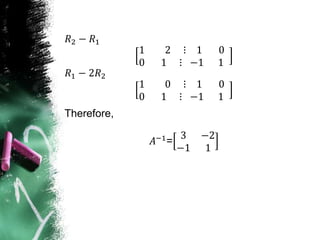The document discusses various methods for solving systems of linear equations, including Gauss elimination, Gauss Jordan, and Cramer's rule. It provides definitions and examples for each method, detailing the steps involved in solving the equations presented. Additionally, it addresses the conditions for unique and infinite solutions in systems of equations.

1. System of Linear Equation
Made By:-
Name/Enrolment no:-
• Nitishkant Dubey- 150860131007
• Feba Daniel- 150860131008
• Vikshit Ganjoo- 150860131009
• Prachi Gite- 150860131010
• Anjani Halpati- 150860131011
Subject code:-2110015

2. Contents
• Gauss Elimination
• Gauss Jordan
• Cramer's Rule

4. Gauss Elimination
Definition:
It is the method in which a row algorithm
that will enable us to analyze any system of
linear equations commonly called Gaussin
Elimination. In other word, A method of
solving a linear system of equations. This is
done by transforming the system's
augmented matrix into reduced row-
echelon form by means of row operations.

5. Example
• Example: Solve the system of linear equation
𝑥1-2𝑥2+3𝑥3=-2, −𝑥1 + 𝑥2 − 2𝑥3=3, 2𝑥1-𝑥2+3𝑥3=3
• Solution: lets apply gauss elimination method for
solving the system.
The augmented matrix of the given system is
1 −2 3 ⋮
−1 1 −2 ⋮
2 −1 3 ⋮
−2
3
3
Let us reduce (i) by row-echelon form by following
way.

6. 𝑅2+𝑅1, 𝑅3 − 2𝑅1
1 −2 3 ⋮
0 −1 1 ⋮
0 3 −3 ⋮
−2
1
7
𝑅2(-1), 𝑅3 − 3𝑅2
1 −2 3 ⋮
0 1 −1 ⋮
0 0 0 ⋮
−2
−1
10
𝑅3/10
1 −2 3 ⋮
0 1 −1 ⋮
0 0 0 ⋮
−2
−1
1
Which is require row equivalent form.
By going back to equations, we get
𝑥1-2𝑥2+3𝑥3=-2, 𝑥2-𝑥3=-1,0=1

8. Gauss Jordan
The method of finding the inverse of an given non-
singular matrix by elementary row transformations
is called gauss Jordan method.
Working Rule:
• [A:I]
• A reduces to 𝐴−1

9. Example
• Example: Find the inverse of matrix.
𝐴 =
1 2
1 3
• Solution: We have to first check about the
existence of 𝐴−1.
𝐴 =
1 2
1 3
= 3 - 2= 1 ≠ 0
Therefore 𝐴−1 exist.
Now,
[A:I] =
1 2 ⋮ 1 0
1 3 ⋮ 0 1

10. 𝑅2 − 𝑅1
1 2 ⋮ 1 0
0 1 ⋮ −1 1
𝑅1 − 2𝑅2
1 0 ⋮ 1 0
0 1 ⋮ −1 1
Therefore,
𝐴−1
=
3 −2
−1 1

12. Cramer’s Rule
• Suppose that we have a square system with n
equation with n equations in the same number
of variables 𝑥1, 𝑥2, … , 𝑥 𝑛 . Then the solutions of
the system has the following cases.
• Case1: If the system has nonzero coefficient
determinant D= det(A), then the system has
unique solution is of the form
x1 =
𝐷1
𝐷
, x2=
𝐷2
𝐷
,……., xn =
𝐷𝑛
𝐷

13. • Case2: If the system has zero coefficient
determinant D= det(A), then we have two
posiibilities as discussed bellow:-
 If at least one of Di is nonzero then the system
has no solution.
 If all Di’s are zero, then the system has infinitely
many solution.

14. Example
• Example: solve the following with Cramer's rule
2x + y + z = 3
x – y – z = 0
x + 2y + z = 0
• Solution: Evaluating each determinant, we get:

15. Cramer's Rule says that x = Dx ÷ D, y = Dy ÷ D,
and z = Dz ÷ D. That is:
x = 3/3 = 1, y = –6/3 = –2, and z = 9/3 = 3